贪心算法是指在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,只做出在某种意义上的局部最优解。贪心算法不是对所有问题都能得到整体最优解,关键是贪心策略的选择,选择的贪心策略必须具备无后效性,即某个状态以前的过程不会影响以后的状态,只与当前状态有关。
有n个需要在同一天使用同一个教室的活动a1,a2,…,an,教室同一时刻只能由一个活动使用。每个活动ai都有一个开始时间si和结束时间fi 。一旦被选择后,活动ai就占据半开时间区间[si,fi)。如果[si,fi]和[sj,fj]互不重叠,ai和aj两个活动就可以被安排在这一天。该问题就是要安排这些活动使得尽量多的活动能不冲突的举行。例如下图所示的活动集合S,其中各项活动按照结束时间单调递增排序。
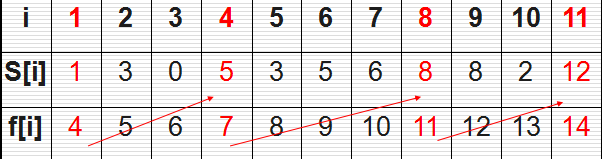
为了方便,我们用不同颜色的线条代表每个活动,线条的长度就是活动所占据的时间段,蓝色的线条表示我们已经选择的活动;红色的线条表示我们没有选择的活动。
如果我们每次都选择开始时间最早的活动,不能得到最优解:
.jpeg)
如果我们每次都选择持续时间最短的活动,不能得到最优解:

我们的贪心策略应该是每次选取结束时间最早的活动, 按这种方法选择相容活动为未安排活动留下尽可能多的时间。
钱币找零
假设1元、2元、5元、10元、20元、50元、100元的纸币分别有c0, c1, c2, c3, c4, c5, c6张。现在要用这些钱来支付K元,至少要用多少张纸币?用贪心算法的思想,很显然,每一步尽可能用面值大的纸币即可。
Lemonade Change
-
At a lemonade stand, each lemonade costs
$5.Customers are standing in a queue to buy from you, and order one at a time (in the order specified by
bills).Each customer will only buy one lemonade and pay with either a
$5,$10, or$20bill. You must provide the correct change to each customer, so that the net transaction is that the customer pays $5.Note that you don’t have any change in hand at first.
Return
trueif and only if you can provide every customer with correct change.Example 1:
1234567Input: [5,5,5,10,20]Output: trueExplanation:From the first 3 customers, we collect three $5 bills in order.From the fourth customer, we collect a $10 bill and give back a $5.From the fifth customer, we give a $10 bill and a $5 bill.Since all customers got correct change, we output true.Example 2:
12Input: [5,5,10]Output: trueExample 3:
12Input: [10,10]Output: falseExample 4:
1234567Input: [5,5,10,10,20]Output: falseExplanation:From the first two customers in order, we collect two $5 bills.For the next two customers in order, we collect a $10 bill and give back a $5 bill.For the last customer, we can't give change of $15 back because we only have two $10 bills.Since not every customer received correct change, the answer is false.
背包问题
我们考虑这样一种背包问题:在选择物品i装入背包时,可以选择物品的一部分,而不一定要全部装入背包。这时便可以使用贪心算法求解了。计算每种物品的单位重量价值作为贪心选择的依据指标,选择单位重量价值最高的物品,将尽可能多的该物品装入背包,依此策略一直地进行下去,直到背包装满为止。在零一背包问题中贪心选择之所以不能得到最优解原因是贪心选择无法保证最终能将背包装满,部分闲置的背包空间使每公斤背包空间的价值降低了。
多机调度
个作业组成的作业集,可由m台相同机器加工处理。要求给出一种作业调度方案,使所给的n个作业在尽可能短的时间内由m台机器加工处理完成。作业不能拆分成更小的子作业;每个作业均可在任何一台机器上加工处理。这个问题是NP完全问题,还没有有效的解法(求最优解),但是可以用贪心选择策略设计出较好的近似算法(求次优解)。当n<=m时,只要将作业时间区间分配给作业即可;当n>m时,首先将n个作业从大到小排序,然后依此顺序将作业分配给空闲的处理机。也就是说从剩下的作业中,选择需要处理时间最长的,然后依次选择处理时间次长的,直到所有的作业全部处理完毕,或者机器不能再处理其他作业为止。如果我们每次是将需要处理时间最短的作业分配给空闲的机器,那么可能就会出现其它所有作业都处理完了只剩所需时间最长的作业在处理的情况,这样势必效率较低。
简单
Score After Flipping Matrix
题目
We have a two dimensional matrix
Awhere each value is0or1.A move consists of choosing any row or column, and toggling each value in that row or column: changing all
0s to1s, and all1s to0s.After making any number of moves, every row of this matrix is interpreted as a binary number, and the score of the matrix is the sum of these numbers.
Return the highest possible score.
Example 1:
12345Input: [[0,0,1,1],[1,0,1,0],[1,1,0,0]]Output: 39Explanation:Toggled to [[1,1,1,1],[1,0,0,1],[1,1,1,1]].0b1111 + 0b1001 + 0b1111 = 15 + 9 + 15 = 39Note:
1 <= A.length <= 201 <= A[0].length <= 20A[i][j]is0or1.
-
贪心算法,我们知道二进制串中越高位的占的比重越大,所以我们可以直接从高到底来判断是否进行 toggling 操作。
首先为行,行中每个数字的权重不一样,从高往低,所以在行中我们只需要对第一位进行判断(即数组第一个数字),当他为0的时候我们要将他变为1 就需要 toggling ,这样可以使这一行数字的二进制串最大。
列中每一列的权重一样,所以我们需要判断这一列中1的个数和0的个数,当0的个数大于1的个数时我们进行 toggling 操作。
代码
12345678910111213141516171819202122232425262728293031323334353637import numpy as npclass Solution:def toggle_row(self,row):for idx in range(len(row)):if row[idx] == 0:row[idx] = 1else:row[idx] = 0return rowdef toggle_col(self,col):for idx in range(len(col)):if col[idx] == 0:col[idx] = 1else:col[idx] = 0return coldef matrixScore(self, A):""":type A: List[List[int]]:rtype: int"""result = 0A = np.array(A)for idx in range(len(A)):if A[idx][0] == 0:A[idx] = self.toggle_row(A[idx])for idx in range(1,len(A[0])):col = A[:,idx]if sum(col) < len(col)/2:A[:, idx] = self.toggle_col(col)for row in A:t = ''for ele in row:t += str(ele)result += int(t,2)return result
Advantage Shuffle
题目
Given two arrays
AandBof equal size, the advantage of A with respect to B is the number of indicesifor whichA[i] > B[i].Return any permutation of
Athat maximizes its advantage with respect toB.Example 1:
12Input: A = [2,7,11,15], B = [1,10,4,11]Output: [2,11,7,15]Example 2:
12Input: A = [12,24,8,32], B = [13,25,32,11]Output: [24,32,8,12]-
题目大意是对于给定两个长度相同的数组$A$和$B$,要求重排$A$,尽量使$A$中每一个元素值都大于$B$中对应元素。
这就是田忌赛马,尽量用小的数去对应对方的最大的数,然后用差距不大的数对应对方数。实现的时候,先对$A$排序,然后对每一个$B$中元素使用
bisect.bisect_right找出离他最近的$A$中的元素,与之对应;如果没有,则使用$A$中最小的与之对应。 代码
1234567891011import bisectclass Solution:def advantageCount(self, A, B):sorted_a = sorted(A)result = []for i in B:idx = bisect.bisect_right(sorted_a,i)if idx == len(sorted_a):result.append(sorted_a.pop(0))else: result.append(sorted_a.pop(idx))return result
Boats to Save People
题目
The
i-th person has weightpeople[i], and each boat can carry a maximum weight oflimit.Each boat carries at most 2 people at the same time, provided the sum of the weight of those people is at most
limit.Return the minimum number of boats to carry every given person. (It is guaranteed each person can be carried by a boat.)
Example 1:
123Input: people = [1,2], limit = 3Output: 1Explanation: 1 boat (1, 2)Example 2:
123Input: people = [3,2,2,1], limit = 3Output: 3Explanation: 3 boats (1, 2), (2) and (3)Example 3:
123Input: people = [3,5,3,4], limit = 5Output: 4Explanation: 4 boats (3), (3), (4), (5)-
题目大概是要让一群人过河,每一艘船只能载两个人且承重最多是$limit$。问把所有人送过河所需的最少船只。
贪心策略:把体重排序之后,每次选择最重的人和最轻的人,如果体重之和在船只承重范围内,则一次送走两个人;否则,只能送走最重的那个人。
代码
12345678910111213class Solution:def numRescueBoats(self, people, limit):people = sorted(people)front,back = 0,len(people)-1count = 0while front<=back:if people[front] + people[back] <= limit:front += 1back -= 1else:back -= 1count += 1return count
Is Subsequence
题目
Given a string s and a string t, check if s is subsequence of t.
You may assume that there is only lower case English letters in both s and t. t is potentially a very long (length ~= 500,000) string, and s is a short string (<=100).
A subsequence of a string is a new string which is formed from the original string by deleting some (can be none) of the characters without disturbing the relative positions of the remaining characters. (ie,
"ace"is a subsequence of"abcde"while"aec"is not).Example 1:
s ="abc", t ="ahbgdc"Return
true.Example 2:
s ="axc", t ="ahbgdc"Return
false.思路
题意大概是判断一个字符串
s是否为另一个t的子串,一个串的子串:通过删去一些字符得到的字符串。很显然,就从头比较两个字符串,设置两个指针
p1和p2,初始分别指向字符串s和t的首字符。如果相同,则同时移动两个指针指向下一个字符;否则只移动p2指向t的下一个字符,直到找到与p1指向的字符。遍历一遍即可,如果p1不能超过s的最后一个字符,则不能是子串。代码
12345678910111213class Solution:def isSubsequence(self, s, t):if not s: return Truecur_s = 0cur_t = 0ls = len(s)lt = len(t)while cur_s<ls and cur_t<lt:if s[cur_s]==t[cur_t]:cur_s += 1cur_t += 1if cur_s==ls:return Truereturn False
Couples Holding Hands
题目
N couples sit in 2N seats arranged in a row and want to hold hands. We want to know the minimum number of swaps so that every couple is sitting side by side. A swap consists of choosing any two people, then they stand up and switch seats.
The people and seats are represented by an integer from
0to2N-1, the couples are numbered in order, the first couple being(0, 1), the second couple being(2, 3), and so on with the last couple being(2N-2, 2N-1).The couples’ initial seating is given by
row[i]being the value of the person who is initially sitting in the i-th seat.Example 1:
123Input: row = [0, 2, 1, 3]Output: 1Explanation: We only need to swap the second (row[1]) and third (row[2]) person.Example 2:
123Input: row = [3, 2, 0, 1]Output: 0Explanation: All couples are already seated side by side.-
贪心,不过不好证明。从位置0开始,看位置1是否是它的partner,如果是,直接忽略这组couple,如果不是,从后面的数组中,找到partner直接交换,并且记录交换次数一次。遍历完整个数组即为最优解。
代码
1234567891011121314151617181920212223class Solution:def minSwapsCouples(self, row):pos = 0step = 0while pos<len(row):wife = row[pos]husband = row[pos+1]if wife%2==0:if wife+1==husband:passelse:husband_pos = row.index(wife + 1)row[pos + 1], row[husband_pos] = row[husband_pos], row[pos + 1] # 找到husband的位置,交换step += 1else:if wife-1==husband:passelse:husband_pos = row.index(wife - 1)row[pos + 1], row[husband_pos] = row[husband_pos], row[pos + 1] # 找到husband的位置,交换step += 1pos += 2return step
Jump Game
题目
Given an array of non-negative integers, you are initially positioned at the first index of the array.
Each element in the array represents your maximum jump length at that position.
Determine if you are able to reach the last index.
Example 1:
123Input: [2,3,1,1,4]Output: trueExplanation: Jump 1 step from index 0 to 1, then 3 steps to the last index.Example 2:
1234Input: [3,2,1,0,4]Output: falseExplanation: You will always arrive at index 3 no matter what. Its maximumjump length is 0, which makes it impossible to reach the last index.思路
从index=i的位置出发,其能到达的最远位置是 i+nums[i]。那么我们设置一个青蛙能达到的最远位置为reach,如果最后reach大于等于数组的长度,那么可以到达。可是如何更新reach呢?因为reach表示最远可到达,那么我们一遍扫描数组nums,pos从0开始,表示初始位置,那么如果青蛙从当前位置可以达到的下一个位置是pos+nums[pos],那么reach=max(reach, pos+nums[pos])。但是在比较之前,注意reach要大于等于pos,否则青蛙无法跳跃到pos,则肯定无法成功跳跃到最后一步。
代码
123456789class Solution:def canJump(self, nums):reach = 0pos = 0l = len(nums)while pos<=reach and pos<l:reach = max(reach, pos+nums[pos])pos += 1return reach>=l-1
Jump Game II
题目
Given an array of non-negative integers, you are initially positioned at the first index of the array.
Each element in the array represents your maximum jump length at that position.
Your goal is to reach the last index in the minimum number of jumps.
Example:
1234Input: [2,3,1,1,4]Output: 2Explanation: The minimum number of jumps to reach the last index is 2.Jump 1 step from index 0 to 1, then 3 steps to the last index.-
上一道题目的拓展,思路不变,扫描一次,查看当前的pos是否在reach里面。那么这道题的重点是扫描时候需要跳跃?青蛙从pos=0出发,跳跃一次,其一次能到达的最大位置是reach = nums[pos]+pos,那么当前的位置pos大于reach,说明一次跳跃不够,需要再一次跳跃。所以跳跃的条件是 pos>reach。那么第二次跳跃的最大reach是多少呢?青蛙一次跳跃可以到达的地点是pos从1至reach,那么二次跳跃的最大reach是
max_reach = max( max_reach , nums[pos]+pos ) when 1<=pos<=reach
代码
12345678910111213class Solution:def jump(self, nums):reach = 0pos = 0l = len(nums)step = 0last = 0for cur in range(l):if cur>last:step += 1last = reachreach = max(reach, nums[cur]+cur)return step
Gas Station
题目
123456789101112131415161718192021222324252627282930313233343536373839404142There are N gas stations along a circular route, where the amount of gas at station i is gas[i].You have a car with an unlimited gas tank and it costs cost[i] of gas to travel from station i to its next station (i+1). You begin the journey with an empty tank at one of the gas stations.Return the starting gas station's index if you can travel around the circuit once in the clockwise direction, otherwise return -1.Note:If there exists a solution, it is guaranteed to be unique.Both input arrays are non-empty and have the same length.Each element in the input arrays is a non-negative integer.Example 1:Input:gas = [1,2,3,4,5]cost = [3,4,5,1,2]Output: 3Explanation:Start at station 3 (index 3) and fill up with 4 unit of gas. Your tank = 0 + 4 = 4Travel to station 4. Your tank = 4 - 1 + 5 = 8Travel to station 0. Your tank = 8 - 2 + 1 = 7Travel to station 1. Your tank = 7 - 3 + 2 = 6Travel to station 2. Your tank = 6 - 4 + 3 = 5Travel to station 3. The cost is 5. Your gas is just enough to travel back to station 3.Therefore, return 3 as the starting index.Example 2:Input:gas = [2,3,4]cost = [3,4,3]Output: -1Explanation:You can't start at station 0 or 1, as there is not enough gas to travel to the next station.Let's start at station 2 and fill up with 4 unit of gas. Your tank = 0 + 4 = 4Travel to station 0. Your tank = 4 - 3 + 2 = 3Travel to station 1. Your tank = 3 - 3 + 3 = 3You cannot travel back to station 2, as it requires 4 unit of gas but you only have 3.Therefore, you can't travel around the circuit once no matter where you start.-
从index=0的位置出发,如果left = gas[index]-cost[index]大于等于0,说明可以到达下一个地点。那么从下一个地点计算left = left + gas[index]-cost[index],表示用上一次剩下的油和当前地点提供的油,是否可以到达下一个地点,如果大于等于0,则可以。
如果left一直是大于0,那么就可以一直走下去。否则,如果left小于0,那么说明不能继续往下走了,那么记录当前lack=left,将欠下来的油记录下来,同时left=0,从下一个位置重新走,如果最终遍历完数组剩下的油能够弥补之前欠下的,那么可以到达,并返回最后一次开始的位置。
代码
12345678910111213class Solution:def canCompleteCircuit(self, gas, cost):left = 0lack = 0begin = 0l = len(gas)for i in range(l):left += gas[i]-cost[i]if left<0:lack += leftleft = 0begin = i+1return begin if lack+left>=0 else -1
Best Time to Buy and Sell Stock II
题目
123456789101112131415161718192021222324Say you have an array for which the ith element is the price of a given stock on day i.Design an algorithm to find the maximum profit. You may complete as many transactions as you like (i.e., buy one and sell one share of the stock multiple times).Note: You may not engage in multiple transactions at the same time (i.e., you must sell the stock before you buy again).Example 1:Input: [7,1,5,3,6,4]Output: 7Explanation: Buy on day 2 (price = 1) and sell on day 3 (price = 5), profit = 5-1 = 4.Then buy on day 4 (price = 3) and sell on day 5 (price = 6), profit = 6-3 = 3.Example 2:Input: [1,2,3,4,5]Output: 4Explanation: Buy on day 1 (price = 1) and sell on day 5 (price = 5), profit = 5-1 = 4.Note that you cannot buy on day 1, buy on day 2 and sell them later, as you areengaging multiple transactions at the same time. You must sell before buying again.Example 3:Input: [7,6,4,3,1]Output: 0Explanation: In this case, no transaction is done, i.e. max profit = 0.-
股票买卖,当然是低价买入,高价卖出。那么如果今天的价格高于前一天,那么我们就可以赚钱,因为可以前一天买入,今天卖出。如果明日的价格更高,那么可以今日再买入,明天再卖出。
代码
1234567class Solution:def maxProfit(self, prices):profit = 0for i in range(len(prices)-1):if prices[i]<prices[i+1]:profit += prices[i+1] - prices[i]return profit
Best Time to Buy and Sell Stock with Transaction Fee
题目
Your are given an array of integers
prices, for which thei-th element is the price of a given stock on dayi; and a non-negative integerfeerepresenting a transaction fee.You may complete as many transactions as you like, but you need to pay the transaction fee for each transaction. You may not buy more than 1 share of a stock at a time (ie. you must sell the stock share before you buy again.)
Return the maximum profit you can make.
Example 1:
1234Input: prices = [1, 3, 2, 8, 4, 9], fee = 2Output: 8Explanation: The maximum profit can be achieved by:Buying at prices[0] = 1Selling at prices[3] = 8Buying at prices[4] = 4Selling at prices[5] = 9The total profit is ((8 - 1) - 2) + ((9 - 4) - 2) = 8.思路
解法1:题意大概是,可以进行无限次的交易(买入-卖出算一次交易),但是每一次交易需要代价fee。完全就是Best Time to Buy and Sell Stock II,只是多了交易费用。会想用动态规划求解,因为贪心算法比较不明显,dp[i]表示第i天的最大收益,对于每一天,都有两种选择,买进,卖出或者没有操作。说到这里,有点像题目Wiggle Subsequence 设置两个dp数组, dp_buy[i]和dp_sell[i]:
dp_buy[i]表示以当前价格买进stock,可以获取的最大利润
dp_sell[i]表示以当前价格卖出stock,可以获取的最大利润
dp_buy[i] = max( dp_buy[i] , dp_sell[j] - price[i] )
dp_sell[i] = max( dp_sell[i] , dp_buy[j] + price[i] + fee )
解法2:
上述方法的时间复杂度是$O(n^2)$,最终超时。所以,必须只能扫描一遍,$O(n)$复杂度。设置两个全局变量,dp_buy和dp_sell,分别表示在操作prices[i]之前,当前买进和卖出最大的获利,状态更新不变。
代码
1234567891011121314151617181920212223242526####超时import sysclass Solution:def maxProfit(self, prices, fee):l = len(prices)dp_buy = [-sys.maxsize]*ldp_sell = [0]*ldp_buy[0] = -prices[0]for i in range(1,l):for j in range(i):dp_buy[i] = max( dp_buy[i] , dp_sell[j] - prices[i] )dp_sell[i] = max( dp_sell[i] , dp_buy[j] + prices[i] - fee )print(dp_buy,dp_sell)return max(dp_sell)import sysclass Solution:def maxProfit(self, prices, fee):dp_buy = -sys.maxsizedp_sell = 0for i in range(len(prices)):dp_buy = max(dp_buy,dp_sell-prices[i])dp_sell = max(dp_sell,dp_buy + prices[i]-fee)return dp_sell
Non-overlapping Intervals
题目
Given a collection of intervals, find the minimum number of intervals you need to remove to make the rest of the intervals non-overlapping.
Note:
- You may assume the interval’s end point is always bigger than its start point.
- Intervals like [1,2] and [2,3] have borders “touching” but they don’t overlap each other.
Example 1:
123Input: [ [1,2], [2,3], [3,4], [1,3] ]Output: 1Explanation: [1,3] can be removed and the rest of intervals are non-overlapping.Example 2:
123Input: [ [1,2], [1,2], [1,2] ]Output: 2Explanation: You need to remove two [1,2] to make the rest of intervals non-overlapping.Example 3:
123Input: [ [1,2], [2,3] ]Output: 0Explanation: You don't need to remove any of the intervals since they're already non-overla
-
这道题实际上是活动选择问题,这个题可以转化为:给定一些任务,以及它们的开始时间和结束时间。并且给定一段时间,尽可能安排多的任务。很容易想到,我们希望尽可能的安排比较早结束的任务(也就是end比较小的),然后是考虑start紧跟上一个end的任务,最后,总任务数量,减去排好的任务,就是要删除的任务。
代码
123456789101112131415161718192021# Definition for an interval.# class Interval:# def __init__(self, s=0, e=0):# self.start = s# self.end = eclass Solution:def eraseOverlapIntervals(self, intervals):""":type intervals: List[Interval]:rtype: int"""if not intervals: return 0sort_intervals = sorted(intervals,key=lambda x:x.end)count = 1end = sort_intervals[0].endfor interval in sort_intervals:if interval.start >= end:count += 1end = interval.endreturn len(intervals)-count
Partition Labels
题目
A string
Sof lowercase letters is given. We want to partition this string into as many parts as possible so that each letter appears in at most one part, and return a list of integers representing the size of these parts.Example 1:
123456Input: S = "ababcbacadefegdehijhklij"Output: [9,7,8]Explanation:The partition is "ababcbaca", "defegde", "hijhklij".This is a partition so that each letter appears in at most one part.A partition like "ababcbacadefegde", "hijhklij" is incorrect, because it splits S into less part-
å题目大意:把字符串分割成尽量多的不重叠子串,输出子串的长度数组。要求相同字符只能出现在一个子串中。
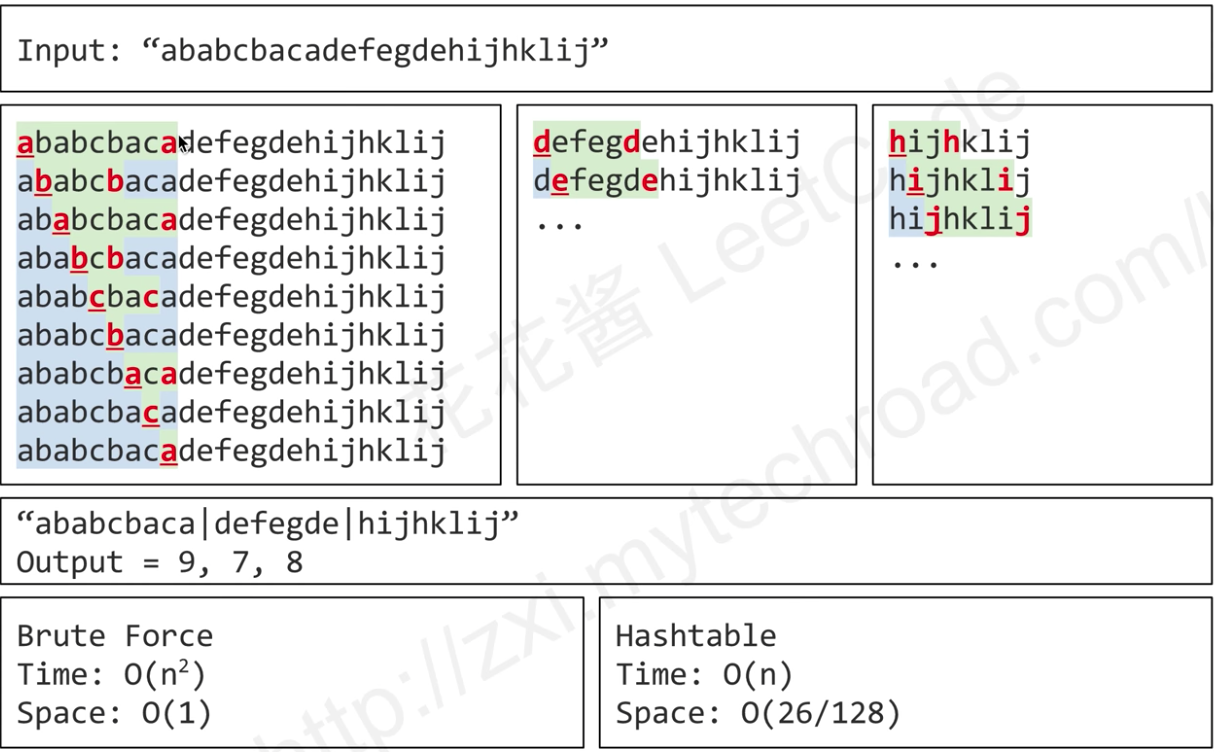
解法一是暴力检索。从第一个字符开始
a, 因为a只能出现在当前子串中,所以我们就要找到a最后出现的位置,这样我们就有了暂时的第一个子串start=0,end=9.继续扫描,发现b的结束位置是5,所以b被包含在start=0,end=9子串中,继续下去,我们就找到了第一个子串start=0,end=9。同样start=start+1,重新扫描,找下一个子串。start=10,end=15. 继续扫描,发现
e的结束位置是end=17,则更新子串start=10,end=17。以此类推。可以发现,我们需要双重循环,外循环扫描一次input字符串,内循环扫描candidate子串,所以是$O(n^2)$的时间复杂度,但是我们没有使用额外空间。
解法二借用哈希表,使用空间代价获取时间效用。可以发现,内循环用于找到每个字符串的结束位置,所以我们使用哈希表将结束位置存储起来,这样时间复杂度就降为$O(n)$. 至于空间复杂度,如果哈希表使用26个字母表示,则空间复杂度是$O(26)$。如果使用ASCII表示,则是$O(128)$.
代码
1234567891011121314class Solution:def partitionLabels(self, S):end_pos = {}for i in range(len(S)):end_pos[S[i]] = istart = 0end = 0re = []for i in range(len(S)):end=max(end,end_pos[S[i]])if end==i:re.append(end-start+1)start = end+1return re
Split Array into Consecutive Subsequences
题目
You are given an integer array sorted in ascending order (may contain duplicates), you need to split them into several subsequences, where each subsequences consist of at least 3 consecutive integers. Return whether you can make such a split.
Example 1:
123456Input: [1,2,3,3,4,5]Output: TrueExplanation:You can split them into two consecutive subsequences :1, 2, 33, 4, 5Example 2:
123456Input: [1,2,3,3,4,4,5,5]Output: TrueExplanation:You can split them into two consecutive subsequences :1, 2, 3, 4, 53, 4, 5Example 3:
12Input: [1,2,3,4,4,5]Output: False-
题意大概就是:不减数组,能否将数组分割,使得到的子数组长度至少3,且是数组中的元素是连续的。
比如
[1,2,3,3,4,5],对于每一位数字,都有两种情况,一个是作为新数组的开头,二是作为已知数组的后续元素。对于第一种情况,如果数字是i且作为开头,那么为了有解,必须存在i+1和i+2,这样新数组才有可能。那么对于后续元素i+3,那么它可以加入[i, i+1, i+2]之中,或者作为开头[i+3]且判断i+4,i+5是否存在。那么基于贪心,是加入已知数组作为后续,因为如果两个数组[i,i+1,i+2]和[i+3,i+4,i+5]可以合并[i,i+1,i+2, i+3,i+4,i+5]。而且如果不存在i+4或者i+5,就不能两个数组,但是仍然可以添加到已知数组中。所以我们需要一个continue[i]数组,初始是0,如果i可以添加到已经数组中,则+1。比如已知数组[i,i+1,i+2],那么我们就设置continue[i+3] += 1.这样我们扫描的时候,先检查continue数组,如果该元素对应的continue数组是否为0,如果是0,那么说明没有已知数组可以让该元素插入,则得开盘新数组让该元素作为开头,同时检查i+1和i+2是否存在;如果不为0,那么就说明可以添加到已知数组,continue -= 1。
[1,2,3,3,4,5]。我们借助一个哈希表frequency{ }存储每个数字的出现次数,continue[0,0,0,0,0,0 ]
frequency[1] = 1, frequency[2]=1, frequency[3]=2, frequency[4]=1,frequency[5]=1
第一个数字是
1, frequency[1]=1,则说明它要么插入已知数组,要么开辟新数组。因为continue是0,则开辟新数组,同时检查是否有i+1,i+2,即2和3。都有,说明我们有了一下新数组[1,2,3],同时如果有4,则可以插入[1,2,3]中。continue[0,0,0,0,1,0],frequency[1] = 0, frequency[2]=0, frequency[3]=1, frequency[4]=1,frequency[5]=1
第二个数字是2,但是frequency[2]=0,跳过。
第三个数字是3,frequency[3]=1,单数continue[3]=0,不能插入已知数组,重新开辟数组,同时frequency[4]和frequency[5]等于1,则得到第二个数字[3,4,5].
代码
12345678910111213141516171819import collectionsclass Solution:def isPossible(self, nums):frequency = collections.Counter(nums)continue_ = collections.defaultdict(int)for ele in nums:if frequency[ele]==0:continueif continue_[ele]>0:frequency[ele] -= 1continue_[ele] -= 1continue_[ele+1] += 1 ####impotantelif frequency[ele+1]>0 and frequency[ele+2]>0:frequency[ele] -= 1frequency[ele+1] -= 1frequency[ele+2] -= 1continue_[ele+3] += 1else:return Falsereturn True
Dota2 Senate
题目
In the world of Dota2, there are two parties: the
Radiantand theDire.The Dota2 senate consists of senators coming from two parties. Now the senate wants to make a decision about a change in the Dota2 game. The voting for this change is a round-based procedure. In each round, each senator can exercise
oneof the two rights:Ban one senator's right:
A senator can make another senator lose all his rights in this and all the following rounds.Announce the victory:
If this senator found the senators who still have rights to vote are all from the same party, he can announce the victory and make the decision about the change in the game.
Given a string representing each senator’s party belonging. The character ‘R’ and ‘D’ represent the
Radiantparty and theDireparty respectively. Then if there arensenators, the size of the given string will ben.The round-based procedure starts from the first senator to the last senator in the given order. This procedure will last until the end of voting. All the senators who have lost their rights will be skipped during the procedure.
Suppose every senator is smart enough and will play the best strategy for his own party, you need to predict which party will finally announce the victory and make the change in the Dota2 game. The output should be
RadiantorDire.Example 1:
12345Input: "RD"Output: "Radiant"Explanation: The first senator comes from Radiant and he can just ban the next senator's right in the round 1.And the second senator can't exercise any rights any more since his right has been banned.And in the round 2, the first senator can just announce the victory since he is the only guy in the senate who can vote.Example 2:
1234567Input: "RDD"Output: "Dire"Explanation:The first senator comes from Radiant and he can just ban the next senator's right in the round 1.And the second senator can't exercise any rights anymore since his right has been banned.And the third senator comes from Dire and he can ban the first senator's right in the round 1.And in the round 2, the third senator can just announce the victory since he is the only思路
简单而言就是比较哪一方的人多,如果一样多,就看哪一方的人比较前面,极端情况就是
R的人全部在前面,D的人全部在后面,这样D的人完全没有机会选择或者发言。所以,就比较顺序了。从序列第一个先查看,假设是
R,那么找到第一个D,移除,但是R仍然保留在序列中。继续扫描下一个,类似操作。扫描完之后,会发现序列中剩下一些,继续从头扫描,直到序列剩下一个。为了简化操作,在移除对手之后,我们将该Senate移到序列的最后,即其位置设置为(index+l)。同时移除时有查找对手index的操作,我们设置两个数组保存双方的index,开始时两个数组都将第一个元素pop,比较,较小的index获胜,将它移动到序列的最后,操作就是append(index+l)。代码
123456789101112131415161718class Solution:def predictPartyVictory(self, senate):d_queue = []r_queue = []l = len(senate)for i in range(l):if senate[i]=='R':r_queue.append(i)else:d_queue.append(i)while d_queue and r_queue:d_index = d_queue.pop(0)r_index = r_queue.pop(0)if d_index>r_index:r_queue.append(r_index+l)else:d_queue.append(d_index+l)return 'Radiant' if r_queue else 'Dire'
Minimum Number of Arrows to Burst Balloons
题目
There are a number of spherical balloons spread in two-dimensional space. For each balloon, provided input is the start and end coordinates of the horizontal diameter. Since it’s horizontal, y-coordinates don’t matter and hence the x-coordinates of start and end of the diameter suffice. Start is always smaller than end. There will be at most 104 balloons.
An arrow can be shot up exactly vertically from different points along the x-axis. A balloon with xstart and xendbursts by an arrow shot at x if xstart ≤ x ≤ xend. There is no limit to the number of arrows that can be shot. An arrow once shot keeps travelling up infinitely. The problem is to find the minimum number of arrows that must be shot to burst all balloons.
Example:
12345678Input:[[10,16], [2,8], [1,6], [7,12]]Output:2Explanation:One way is to shoot one arrow for example at x = 6 (bursting the balloons [2,8] and [1,6]) and another arrow at x = 11 (bursting the other two balloons).思路
题目大概:给你一堆气球,这些气球沿X轴方向摆放,每个气球大小可能不同,一个气球占据的区间可以表示为[Xstart,Xend],气球可以重叠摆放。一支坐标为x的箭,可以扎破所有满足 Xstart <= x <= Xend 的气球,求出最少射几支箭可以将所有气球扎破。
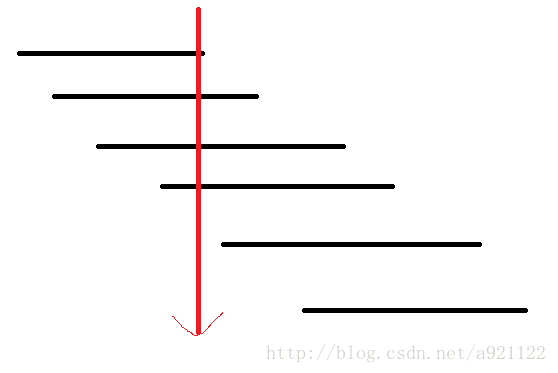
题目的图像表示如上,将气球按照end排序,那么只要前一个气球的end不小于下一个气球的start,则一箭可以同时刺穿。
代码
1234567891011class Solution:def findMinArrowShots(self, points):sort_points = sorted(points,key=lambda x:x[1])if not points:return 0count = 1end = sort_points[0][1]for balloon in sort_points[1:]:if end<balloon[0]:count += 1end = balloon[1]return count
中等
Walking Robot Simulation
题目
A robot on an infinite grid starts at point (0, 0) and faces north. The robot can receive one of three possible types of commands:
-2: turn left 90 degrees-1: turn right 90 degrees1 <= x <= 9: move forwardxunits
Some of the grid squares are obstacles.
The
i-th obstacle is at grid point(obstacles[i][0], obstacles[i][1])If the robot would try to move onto them, the robot stays on the previous grid square instead (but still continues following the rest of the route.)
Return the square of the maximum Euclidean distance that the robot will be from the origin.
Example 1:
123Input: commands = [4,-1,3], obstacles = []Output: 25Explanation: robot will go to (3, 4)Example 2:
123Input: commands = [4,-1,4,-2,4], obstacles = [[2,4]]Output: 65Explanation: robot will be stuck at (1, 4) before turning left and going to (1, 8)思路
问题大意:有一个机器人在无限大的平面上,初始时面对正北方向位于$(0,0)$。机器人接受一系列指令:-2则要左转;-1则要右转;1-9之间的数字则要前进相应的步数。但是该平面上有一些障碍$(i,j)$,如果机器人在行进过程中遇到了障碍,则停留在当前位置不动。求机器人能到达的最大欧氏距离。
该问题有两个难点:一个是方向如何表示,二是如何表示方向的改变。
假如现在在$(0,0)$,如果前进$a$个长度:
假设向$N$前进,则前进后的位置是$N(0,a)=N(0,0)+(0,a)$
假设现在在E,前进后的位置是E(a,0)=E(0,0)+(a,0)$
假设现在在$S$,则前进后的位置是$S(a,0)=S(0,0)+(0,-a)$
假设现在在W,则前进后的位置是$W(a,0)=E(0,0)+(-a,0)$
基于此,我们可以N,E,S,W四个方向转化为$[(0,1),(1,0),(0,-1),(-1,0)]$
那么该如何改变方向呢?即如何选择上述四个方向呢?
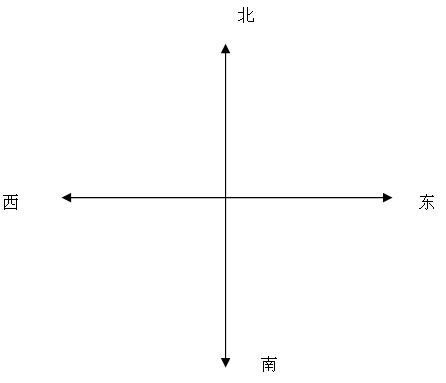
可以发现无论当前处于东南西北的哪一个方向,接受到指令$-2$,你选择左边的方向,$-1$则选择右边的方向。如果用$direction$表示当前方向,则-2时,你更新你的方向为
$ direction = (direction-1)%4$;-1时,更新$direction = (direction + 1) % 4$ 。
-
123456789101112131415161718192021222324class Solution:def robotSim(self, commands, obstacles):""":type commands: List[int]:type obstacles: List[List[int]]:rtype: int"""directions = [(0,1),(1,0),(0,-1),(-1,0)] # N,E,S,Wobstacles = set(map(tuple,obstacles))max_dis,x,y,direction = 0,0,0,0for command in commands:if command == -2:direction = (direction-1)%4elif command == -1 :direction = (direction + 1) % 4else:x_offset,y_offset = directions[direction][0],directions[direction][1]while command>0:if (x+x_offset,y+y_offset) not in obstacles:x += x_offsety += y_offsetcommand -= 1max_dis = max(max_dis,x**2+y**2)return max_dis
Queue Reconstruction by Height
题目
12345678910111213Suppose you have a random list of people standing in a queue. Each person is described by a pair of integers (h, k), where h is the height of the person and k is the number of people in front of this person who have a height greater than or equal to h. Write an algorithm to reconstruct the queue.Note:The number of people is less than 1,100.ExampleInput:[[7,0], [4,4], [7,1], [5,0], [6,1], [5,2]]Output:[[5,0], [7,0], [5,2], [6,1], [4,4], [7,1]]-
题目大致的意思是:每一个由一组整数(h, k)表示,h是其身高,k是队列之中身高不低于h的人数。现在要重构这个队列。
首先,这个题目类似于作业调度,需要根据(h,k)排序,问题是先根据哪一个排序呢?答案是以h排序,使身高从大到小排序,即先为身高有优势的在队列中找到位置,这样,身高比较矮的人在队列中的位置就是任意了,因为无论他们不会对身高高的人造成影响,即已经找到位置的身高优势的人,不会因为矮的人的插入而重新排列。而对于身高相同的人,显然是k值小的先插入。
所以,先根据h排序,h相同时根据k排序。
针对上述例子:
根据h排序之后,[7,0], [7,1], [6,1], [5,0], [5,2], [4,4]
根据k排序之后,已经有序
对于第一个人[7,0],根据k值插入数组[ [7,0] ]
[7,1],k=1插入[ [7,0] , [7,1] ]
[6,1], k=1插入[[7,0],[6,1],[7,1]]需要注意的是,无论[6,1]插入位置,都不会对已经插入的元素造成影响
…
代码
12345678class Solution:def reconstructQueue(self, people):new_people = sorted(people,key=lambda x:x[1])new_people = sorted(new_people,key=lambda x:x[0],reverse=True)queue = []for i in new_people:queue.insert(i[1],i)return queue
Remove K Digits
题目
Given a non-negative integer num represented as a string, remove k digits from the number so that the new number is the smallest possible.
Note:
- The length of num is less than 10002 and will be ≥ k.
- The given num does not contain any leading zero.
Example 1:
123Input: num = "1432219", k = 3Output: "1219"Explanation: Remove the three digits 4, 3, and 2 to form the new number 1219 which is the smallest.Example 2:
123Input: num = "10200", k = 1Output: "200"Explanation: Remove the leading 1 and the number is 200. Note that the output must not contain leading zeroes.Example 3:
123Input: num = "10", k = 2Output: "0"Explanation: Remove all the digits from the number and it is left with nothing which is 0.思路
首先,理解一下什么样的数才是尽可能最小的。
尽量维持一个从左至右递增的顺序。否则如果有num[i]>nums[i+1],即出现了递减,则删除num[i+1]之前的数字,使维持递增。扫描结束之后,得到递增数列,但是删除的数字未满k个,则从后往前删除使实现删除k个数字。值得一提的是,数字的首位不能是0.
为实现递增,我们借助栈,如果出现当前元素小于栈顶,则持续出栈,直到栈顶小于当前元素,然后入栈。
-
12345678910111213141516171819class Solution:def removeKdigits(self, num, k):l = len(num)stack = []cur = 0while cur < l :while stack and stack[-1] > num[cur] and k > 0:stack.pop()k -= 1stack.append(num[cur])cur += 1while k > 0:stack.pop()k -= 1re = ""while stack:re = stack.pop() + rereturn str(int(re)) if re else str(0)
Monotone Increasing Digits
题目
Given a non-negative integer
N, find the largest number that is less than or equal toNwith monotone increasing digits.(Recall that an integer has monotone increasing digits if and only if each pair of adjacent digits
xandysatisfyx <= y.)Example 1:
12Input: N = 10Output: 9Example 2:
12Input: N = 1234Output: 1234Example 3:
12Input: N = 332Output: 299思路
首先,题目有一个模棱两可的地方, monotone increasing意思是单调递增,即不减,所以相等也可以。即
22也是满足 monotone increasing的。所以我们扫描一次input,找到第一个下降的位置,比如
668841,开始下降的index=3。正常是num[index] = num[index]-1,然后后面全部变成9,即668799。显然有问题,因88的存在and减法操作使出现下降。所以,在找到开始下降的index之后,往前扫描,直到找到第一个num[index]的数字,然后将该数字减法1,后面的全部翻转为9。编程的时候,遇到一个问题就是Python中string的操作。如果num_str = str(num),那么num_str就是常量,常量不可以修改,即num_str[i] = ‘a’,是会报错的。可以使用string连接操作
+,或者replace等。代码
12345678910111213141516class Solution:def monotoneIncreasingDigits(self, N):num = list(str(N))end = len(num)flag = Truefor i in range(len(num)-1):if num[i]>num[i+1]:flag=Falseend = ibreakif flag:return Nwhile end>0 and num[end]==num[end-1]:end-=1num[end] = str(int(num[end]) - 1)num = ''.join(num[:end+1]) + '9'*(len(num)-end-1)return int(num)
Task Scheduler
题目
Given a char array representing tasks CPU need to do. It contains capital letters A to Z where different letters represent different tasks.Tasks could be done without original order. Each task could be done in one interval. For each interval, CPU could finish one task or just be idle.
However, there is a non-negative cooling interval n that means between two same tasks, there must be at least n intervals that CPU are doing different tasks or just be idle.
You need to return the least number of intervals the CPU will take to finish all the given tasks.
Example 1:
123Input: tasks = ["A","A","A","B","B","B"], n = 2Output: 8Explanation: A -> B -> idle -> A -> B -> idle -> A -> B.思路
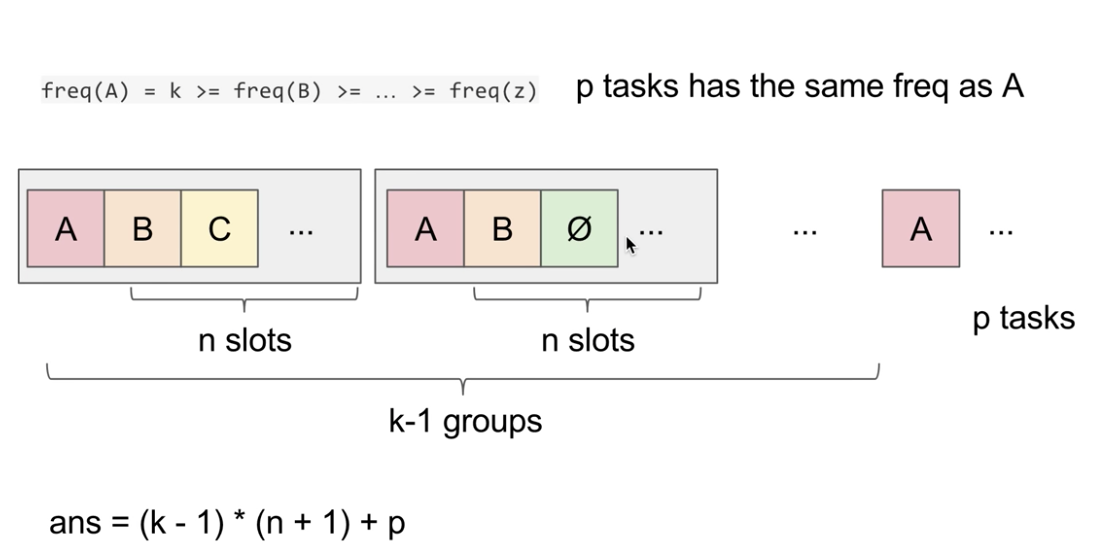
题目大概就是模拟CPU任务分配,A 到 Z表示不同的任务,任务可以以不同顺序进行。每个任务可以在一个时间间隔中完成。对于一个时间间隔,CPU可以执行一个任务或者是闲置。但是,两个同样的任务之间需要有 n 个冷却时间,也就是说假如A执行后,那么未来n个时间间隔内,A是不允许再执行的。
自然的,我们找出frequency最大的字符,因为中间相隔n个字符,以
AAABB为例,那么我们可以有模板AXX|AXX|A,频率少的字符填充,即代替X。如上图所示,因为A出现次数最多,那么我们构造k-1个模板,每个模板大小是n+1,至于最后一个模板,其长度是:频率为k的字符个数。所以,最终的长度是(k-1)*(n+1)+p.但是有一种特殊情况,考虑上述模板,中间填充的永远只有n个字符,如果字符串是
AAAABBBCCCDDD,n=2,我们的模板是AXX|AXX|AXX|A,得到的长度是(k-1)(n+1)+p=(4-1)*(2+1)+1=10。但是,实际上,字符长度是13,正确排列是$ABCD|ABCD|ABCD|A$,可以看出中间的填充是n=3.所以,返回的结果应该是max( len(str) , (k-1)(n+1)+p )
代码
1234567891011121314import collectionsclass Solution:def leastInterval(self, tasks, n):frequency = collections.Counter(tasks)sort_fre = sorted(frequency.items(),key=lambda x:x[1]) #对(key-value)字典排序,以value的大小排序# 找k值k = sort_fre[-1][1]# 找p值p = 1pos = len(sort_fre)-2while pos>=0 and sort_fre[pos][1]==k:pos -= 1p += 1return max(len(tasks),(k-1)*(n+1)+p)
高级
Candy
题目
There are N children standing in a line. Each child is assigned a rating value.
You are giving candies to these children subjected to the following requirements:
- Each child must have at least one candy.
- Children with a higher rating get more candies than their neighbors.
What is the minimum candies you must give?
Example 1:
123Input: [1,0,2]Output: 5Explanation: You can allocate to the first, second and third child with 2, 1, 2 candies respectively.Example 2:
1234Input: [1,2,2]Output: 4Explanation: You can allocate to the first, second and third child with 1, 2, 1 candies respectively.The third child gets 1 candy because it satisfies the above two conditions.思路
题意大概是:为每个小孩分配至少一个糖果,且等级高的小孩分配到的糖果比其左右小孩得到的多。
初始化candy数组全1,使每个孩子都有糖果。重点是如果根据等级再分配糖果。两遍扫描,一次从左到右,只要当前的小孩的等级比他左边的小孩高,就根据其左边孩子的糖果数量多分配一个糖果candy_left;二次扫描,只要当前的小孩的等级比他右边的小孩高,就根据其右边孩子的糖果数量多分配一个糖果candy_right,最终的糖果数量是max(candy_left,candy_right).
代码
1234567891011121314151617class Solution:def candy(self, ratings):l = len(ratings)candy = [1]*lfor i in range(1,l):left_child = ratings[i-1]right_child = ratings[i]if right_child>left_child:candy[i] = candy[i-1]+1pos = l-2while pos>-1:left_child = ratings[pos]right_child = ratings[pos+1]if left_child>right_child:candy[pos] = max(candy[pos],candy[pos+1]+1)pos -= 1return sum(candy)
Remove Duplicate Letters
题目
Given a string which contains only lowercase letters, remove duplicate letters so that every letter appear once and only once. You must make sure your result is the smallest in lexicographical order among all possible results.
Example 1:
12Input: "bcabc"Output: "abc"Example 2:
12Input: "cbacdcbc"Output: "acdb"-
枚举字符串前缀,直到遇到首个唯一字符为止,从前缀中挑选出最小的字符作为首字符。
然后从剩余字符串中移除所有与首字母相同的字母。
重复此过程,直到选出所有唯一字符为止。时间复杂度是$O(k*n)$,$k$是字符串中不同的字符个数, $n$是字符串长度。
代码
12345678910111213141516import collectionsclass Solution:def removeDuplicateLetters(self, s):ans = ''for i in range(len(set(s))):front,index = s[0],0s_counter = collections.Counter(s)for pos,val in enumerate(s):if front>val: #找前缀中字典序小的字母front,index = val,posif s_counter[val]==1: #字符串出现首个唯一字符breaks_counter[val] -= 1ans += fronts = s[index+1:].replace(front,'')return ans
Create Maximum Number
题目
Given two arrays of length
mandnwith digits0-9representing two numbers. Create the maximum number of lengthk <= m + nfrom digits of the two. The relative order of the digits from the same array must be preserved. Return an array of thekdigits.Note: You should try to optimize your time and space complexity.
Example 1:
123456Input:nums1 = [3, 4, 6, 5]nums2 = [9, 1, 2, 5, 8, 3]k = 5Output:[9, 8, 6, 5, 3]Example 2:
123456Input:nums1 = [6, 7]nums2 = [6, 0, 4]k = 5Output:[6, 7, 6, 0, 4]Example 3:
123456Input:nums1 = [3, 9]nums2 = [8, 9]k = 3Output:[9, 8, 9]-
题意大概就是:给定两个数组,从数组中共选出k个元素,使构成的值是最大的,要求选出的元素相对顺序不能改变。
我们先考虑一个数组的情况,即如何从一个数组中选出k个元素,在不改变元素顺序的情况下,组合得到的值最大。贪心方法,使用一个栈,扫描一次数组,如果栈空或者当前的元素值比栈顶大,则持续出栈直到栈顶元素比较大。有个要求就是为了保证最后有k个数字,我们最多只能出栈len(num)-k个元素,具体过程在下图的左上角, 时间复杂度是$O(n)$.
接下来,我们考虑另一个问题,给定两个数组,在不考虑k的限制,即如何用两个数组排列出最大的值。那么显然是贪心了,同时扫描两个数组,分别比较数组的第一个值,选择大值作为新值的一部分,然后弹出该值,继续扫描。
那么将上述两个步骤合并就能解决我们的问题了。因为要选择k个,那么在第一个数组中选择i个,第一个数组中选择(k-i)个,得到的两个子数组构成的值都是相对最优的;那么再将这两个子数组合并,就得到了k长度的解。
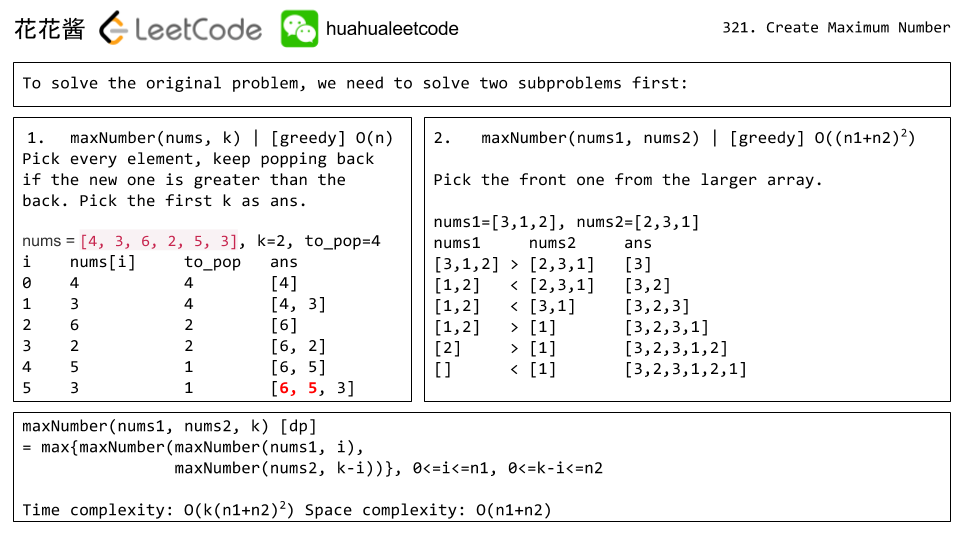
代码
12345678910111213141516171819202122232425262728293031323334353637383940class Solution:# 从数组中选择m个数,使m个数的组合最大def subNumber(self, nums, m):max_pop = len(nums) - m # 最多抛弃的个数pop_num = 0 # 记录当前已经抛弃的数目cur_pos = 0result = []#必须比较数组,而不是数组的数字,为了防止【6,7】和【6,0,1】如果第一个相等,必须比较第二个数字while cur_pos < len(nums):if pop_num < max_pop and result and result[-1] < nums[cur_pos]:pop_num += 1result.pop()else:result.append(nums[cur_pos])cur_pos += 1return result[:m] # 返回前m个数# 合并两个数组,使组合得到最大数def merge_two_nums(self, nums1, nums2):result = []while len(nums1) and len(nums2):if nums1>nums2:result.append(nums1.pop(0))else:result.append(nums2.pop(0))if not len(nums1):result.extend(nums2)else:result.extend(nums1)return resultdef maxNumber(self, nums1, nums2, k):result = []for i in range(k + 1):if i > len(nums1) or (k - i) > len(nums2):continuesubnum1 = self.subNumber(nums1, i)subnum2 = self.subNumber(nums2, k - i)result = max(result, self.merge_two_nums(subnum1, subnum2))return result
Set Intersection Size At Least Two
题目
An integer interval
[a, b](for integersa < b) is a set of all consecutive integers fromatob, includingaandb.Find the minimum size of a set S such that for every integer interval A in
intervals, the intersection of S with A has size at least 2.Example 1:
123456Input: intervals = [[1, 3], [1, 4], [2, 5], [3, 5]]Output: 3Explanation:Consider the set S = {2, 3, 4}. For each interval, there are at least 2 elements from S in the interval.Also, there isn't a smaller size set that fulfills the above condition.Thus, we output the size of this set, which is 3.Example 2:
1234Input: intervals = [[1, 2], [2, 3], [2, 4], [4, 5]]Output: 5Explanation:An example of a minimum sized set is {1, 2, 3, 4, 5}.-
题意大概是:每个连续整数间隔数组都由两个数表示:
a表示连续整数的开始,b表示连续整数的结束。现在给出一堆这样的连续整数间隔,需要找到一个最小的数组,使该数组与每个连续数组都至少有两个数是相同的,不要求该数组是由连续整数构成。也就是说我们需要维护一个动态数组,那么该数组与已知间隔数组会有三种情况:
- 二者没有交集,那么我们就需要从当前间隔数组中取出两个数字加入动态数组;为了尽可能少使用数字,我们取当前间隔中的最大两个数字,因为这样更有可能与后面的间隔有交集。
- 二者有一个交集,那么这个交集一定是间隔的起始位置,则我们只需要选取一个数字加入动态数组,根据上面分析,我们选择最大的数字,即间隔的结束位置。
- 二者有多于一个的交集,则不做任何处理
所以在代码实现时,我们设置一个初始化一个数组为
[-1,-1],给区间按照结束位置排序,然后遍历每个区间,如果区间的开始位置小于等于动态数组的倒数第二个元素,则表示覆盖元素大于1,跳过;如果区间的开始位置小于等于动态数组的最后一个元素,即区间的开始位置介在动态数组的倒数第二个元素和倒数第一个元素之间,则覆盖一个元素,故选择区间的结束位置加入动态数组;如果区间的开始位置大于动态数组的最后一个元素,则没有覆盖,选择区间的结束位置-1,结束位置加入动态数组。 代码
12345678910111213141516class Solution:def intersectionSizeTwo(self, intervals):""":type intervals: List[List[int]]:rtype: int"""intervals = sorted(intervals,key=lambda x:x[1])print(intervals)result = [-1,-1]for interval in intervals:if interval[0] <= result[-2]:continueelif interval[0] <= result[-1]: result.append(interval[1])elif interval[0] > result[-1]:result.append(interval[1]-1)result.append(interval[1])return len(result)-2
Course Schedule III
题目
There are
ndifferent online courses numbered from1ton. Each course has some duration(course length)tand closed ondthday. A course should be taken continuously fortdays and must be finished before or on thedthday. You will start at the1stday.Given
nonline courses represented by pairs(t,d), your task is to find the maximal number of courses that can be taken.Example:
12345678Input: [[100, 200], [200, 1300], [1000, 1250], [2000, 3200]]Output: 3Explanation:There're totally 4 courses, but you can take 3 courses at most:First, take the 1st course, it costs 100 days so you will finish it on the 100th day, and ready to take the next course on the 101st day.Second, take the 3rd course, it costs 1000 days so you will finish it on the 1100th day, and ready to take the next course on the 1101st day.Third, take the 2nd course, it costs 200 days so you will finish it on the 1300th day.The 4th course cannot be taken now, since you will finish it on the 3300th day, which exceeds the closed date.-
题目大意:$n$个课程,每一个课程使用$(t,d)$表示,其中$t$是课程所需时间,$d$表示课程必须在$d$之前完成。如何选课才能选到最多的课程?
我们的贪心选择是 - 选择截止日期越早的课程。比如(300,1000)和(500,600),我们可以先选择(500,600),这样课程结束时间是500<600。然后选择(300,1000),这样课程结束时间是500+300 < 1000。选择2门课。
而非优先选择所需时间最短的课程。优选选择课时短的(300,1000),结束时间是300. 如果再选择(500,600),上完课的时间就是 300+500 > 600,就不能选了。
但是,为了防止这种情况:
[[5,5],[4,6],[2,6]],如果单纯用上述方法,则返回1。实际上,我们需要一个优先队列,将选择的课程按照持续时间排列,扫描课程,先吸收入优先队列,更新start时间;然后判断该课程是否合理,如果不合理,则从队列中选择持续时间最长的课程,抛弃之。 -
12345678910111213141516import heapqclass Solution:def scheduleCourse(self, courses):if not courses: return 0sel_c = []sorted_c = sorted(courses,key=lambda x:x[1])start = 0for c in sorted_c:duration = c[0]end = c[1]heapq.heappush(sel_c,-duration)start = duration + startif start > end:d = heapq.heappop(sel_c)start += dreturn len(sel_c)
Patching Array
题目
Given a sorted positive integer array nums and an integer n, add/patch elements to the array such that any number in range
[1, n]inclusive can be formed by the sum of some elements in the array. Return the minimum number of patches required.Example 1:
1234567Input: nums = [1,3], n = 6Output: 1Explanation:Combinations of nums are [1], [3], [1,3], which form possible sums of: 1, 3, 4.Now if we add/patch 2 to nums, the combinations are: [1], [2], [3], [1,3], [2,3], [1,2,3].Possible sums are 1, 2, 3, 4, 5, 6, which now covers the range [1, 6].So we only need 1 patch.Example 2:
123Input: nums = [1,5,10], n = 20Output: 2Explanation: The two patches can be [2, 4].Example 3:
12Input: nums = [1,2,2], n = 5Output: 0-
题意大概是:给定一个数组和一个目标值
n,要求往数组中增加最少的元素,使数组中几个元素的和可以表示[1,n]范围内的数字.我们设置一个变量
known_num表示当前数字可以表示的最大[1,known_num)。扫描一遍数组,如果当前的元素不比known_num大,则我们可以更新我们的表示范围[1,known_num + ele_;如果当前的元素比known_num大,那么我们需要添加元素known_num,更新表示范围[1,known_num*2)。 代码
12345678910111213class Solution:def minPatches(self, nums, n):known_num = 1add_num = 0pos = 0while known_num-1 < n:if pos < len(nums) and nums[pos] <= known_num:known_num += nums[pos]pos += 1else:known_num *= 2add_num += 1return add_num
Reorganize String
题目
Given a string
S, check if the letters can be rearranged so that two characters that are adjacent to each other are not the same.If possible, output any possible result. If not possible, return the empty string.
Example 1:
12Input: S = "aab"Output: "aba"Example 2:
12Input: S = "aaab"Output: ""-
题目大致说给出一个字符串,要求重排字符顺序,使得相邻的字符总是不同。
首先,我们先找出不能重构字符串的条件:出现最多次的字符的出现次数大于字符串长度的一半,直接返回空字符串。
其次,如果可以重构,我们借助一个优先队列,每次都从中选择出现次数最多的字符构成字符串,如此循环直至优先队列空。
但是,如果
aaaabbcc,优先队列先弹出a,加入重组字符串;然后会继续弹出a,但是如果直接加入重组字符串,则出现相邻的a。所以,这时,我们继续弹出出现次数第二多的字符b,加入重组字符串。 -
12345678910111213141516171819202122232425import collectionsimport heapqclass Solution:def reorganizeString(self, S):s_counter = collections.Counter(S)most_freq = s_counter.most_common(1)if len(S) < most_freq[0][1]*2-1:return ""re_string = ""h = []for k,v in s_counter.items():heapq.heappush(h,(-v,k))while h:v,k = heapq.heappop(h)if not re_string or k != re_string[-1]: # 初始时 或者 重构字符串的最后一个字符串不同于弹出的字符串re_string += kif v != -1 :heapq.heappush(h,(v+1,k))else:v1,k1 = heapq.heappop(h) #弹出出现次数第二多的字符re_string += k1heapq.heappush(h,(v,k))if v1 != -1:heapq.heappush(h,(v1+1,k))return re_string
IPO
题目
Suppose LeetCode will start its IPO soon. In order to sell a good price of its shares to Venture Capital, LeetCode would like to work on some projects to increase its capital before the IPO. Since it has limited resources, it can only finish at most k distinct projects before the IPO. Help LeetCode design the best way to maximize its total capital after finishing at most k distinct projects.
You are given several projects. For each project i, it has a pure profit Pi and a minimum capital of Ci is needed to start the corresponding project. Initially, you have W capital. When you finish a project, you will obtain its pure profit and the profit will be added to your total capital.
To sum up, pick a list of at most k distinct projects from given projects to maximize your final capital, and output your final maximized capital.
Example 1:
123456789Input: k=2, W=0, Profits=[1,2,3], Capital=[0,1,1].Output: 4Explanation: Since your initial capital is 0, you can only start the project indexed 0.After finishing it you will obtain profit 1 and your capital becomes 1.With capital 1, you can either start the project indexed 1 or the project indexed 2.Since you can choose at most 2 projects, you need to finish the project indexed 2 to get the maximum capital.Therefore, output the final maximized capital, which is 0 + 1 + 3 = 4.思路
大概题意是:你有启动资金$W$,并且你只能完成$k$个任务。现有一堆任务,每个任务需要一定的资金启动,一旦任务完成,你就会获得一定的利润,而且该利润可以添加到你的启动资金里。问最终能达到的最大启动资金?
比较直观,先选择任务的启动资金小于等于你当前的启动资金$W$,然后在可以做的任务里选择获利最大的任务去完成,使最大化你的启动资金$W$。
实现的时候,利用一个优先队列,里面存储的是可以做的任务的获利,扫描任务list,一旦发现任务的启动资金小于等于你的$W$,将该任务的获利送入优先队列。
代码
1234567891011121314import heapqclass Solution:def findMaximizedCapital(self, k, W, Profits, Capital):sorted_capital = sorted(zip(Profits,Capital),key=lambda x:x[1])available_task = []pos = 0while k>0:k -= 1while pos<len(sorted_capital) and sorted_capital[pos][1] <= W:heapq.heappush(available_task,-sorted_capital[pos][0])pos += 1if available_task:W -= heapq.heappop(available_task)return W