动态规划
这篇文章详细记录LeetCode上各种难度的动态规划题目。每道题我都给出题目,思路以及Python代码。
入门
如果我们有面值为1元、3元和5元的硬币若干枚,如何用最少的硬币凑够11元? (表面上这道题可以用贪心算法,但贪心算法无法保证可以求出解,比如1元换成2元的时候)
首先我们思考一个问题,如何用最少的硬币凑够i元(i<11)?为什么要这么问呢? 两个原因:1.当我们遇到一个大问题时,总是习惯把问题的规模变小,这样便于分析讨论。 2.这个规模变小后的问题和原来的问题是同质的,除了规模变小,其它的都是一样的, 本质上它还是同一个问题(规模变小后的问题其实是原问题的子问题)。
好了,让我们从最小的i开始吧。当i=0,即我们需要多少个硬币来凑够0元。 由于1,3,5都大于0,即没有比0小的币值,因此凑够0元我们最少需要0个硬币。 (这个分析很傻是不是?别着急,这个思路有利于我们理清动态规划究竟在做些什么。) 这时候我们发现用一个标记来表示这句“凑够0元我们最少需要0个硬币。”会比较方便, 如果一直用纯文字来表述,不出一会儿你就会觉得很绕了。那么, 我们用d(i)=j来表示凑够i元最少需要j个硬币。于是我们已经得到了d(0)=0, 表示凑够0元最小需要0个硬币。当i=1时,只有面值为1元的硬币可用, 因此我们拿起一个面值为1的硬币,接下来只需要凑够0元即可,而这个是已经知道答案的, 即d(0)=0。所以,d(1)=d(1-1)+1=d(0)+1=0+1=1。当i=2时, 仍然只有面值为1的硬币可用,于是我拿起一个面值为1的硬币, 接下来我只需要再凑够2-1=1元即可(记得要用最小的硬币数量),而这个答案也已经知道了。 所以d(2)=d(2-1)+1=d(1)+1=1+1=2。一直到这里,你都可能会觉得,好无聊, 感觉像做小学生的题目似的。因为我们一直都只能操作面值为1的硬币!耐心点, 让我们看看i=3时的情况。当i=3时,我们能用的硬币就有两种了:1元的和3元的( 5元的仍然没用,因为你需要凑的数目是3元!5元太多了亲)。 既然能用的硬币有两种,我就有两种方案。如果我拿了一个1元的硬币,我的目标就变为了: 凑够3-1=2元需要的最少硬币数量。即d(3)=d(3-1)+1=d(2)+1=2+1=3。 这个方案说的是,我拿3个1元的硬币;第二种方案是我拿起一个3元的硬币, 我的目标就变成:凑够3-3=0元需要的最少硬币数量。即d(3)=d(3-3)+1=d(0)+1=0+1=1. 这个方案说的是,我拿1个3元的硬币。好了,这两种方案哪种更优呢? 记得我们可是要用最少的硬币数量来凑够3元的。所以, 选择d(3)=1,怎么来的呢?具体是这样得到的:d(3)=min{d(3-1)+1, d(3-3)+1}。
OK,码了这么多字讲具体的东西,让我们来点抽象的。从以上的文字中, 我们要抽出动态规划里非常重要的两个概念:状态和状态转移方程。
上文中d(i)表示凑够i元需要的最少硬币数量,我们将它定义为该问题的”状态”, 这个状态是怎么找出来的呢?我在另一篇文章 动态规划之背包问题(一)中写过: 根据子问题定义状态。你找到子问题,状态也就浮出水面了。 最终我们要求解的问题,可以用这个状态来表示:d(11),即凑够11元最少需要多少个硬币。 那状态转移方程是什么呢?既然我们用d(i)表示状态,那么状态转移方程自然包含d(i), 上文中包含状态d(i)的方程是:d(3)=min{d(3-1)+1, d(3-3)+1}。没错, 它就是状态转移方程,描述状态之间是如何转移的。当然,我们要对它抽象一下,
d(i)=min{ d(i-vj)+1 },其中i-vj >=0,vj表示第j个硬币的面值;
746.Min Cost Climbing Stairs
题目
On a staircase, the
i-th step has some non-negative costcost[i]assigned (0 indexed).Once you pay the cost, you can either climb one or two steps. You need to find minimum cost to reach the top of the floor, and you can either start from the step with index 0, or the step with index 1.
>
思路
典型动态规划,且只需要一维dp数组维护,考虑到可以从index=0|1开始,所以在dp数组前面插入两个0(因为是加法,乘法则插入1),同时要表示终点,则在dp尾再插入一个0,统计到达top时的cost。
代码
>
70. Climbing Stairs
题意
You are climbing a stair case. It takes n steps to reach to the top.
Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?
>
>
思路
跟上面一题很相似了,同样是一维,也需要在首个插入
代码
53. Maximum Subarray
题意
Given an integer array
nums, find the contiguous subarray (containing at least one number) which has the largest sum and return its sum.
>
思路
一维dp数组,同样在前面插入0,但是返回的时候,要小心不能返回max(dp),而是max(dp[1:]),防止input是[-1,-2].
代码
198. House Robber
题目
You are a professional robber planning to rob houses along a street. Each house has a certain amount of money stashed, the only constraint stopping you from robbing each of them is that adjacent houses have security system connected and it will automatically contact the police if two adjacent houses were broken into on the same night.
Given a list of non-negative integers representing the amount of money of each house, determine the maximum amount of money you can rob tonight without alerting the police.
>
>
思路
dp状态思考错误,dp[i]表示抢到第i个房子时,目前获取的最大利润
dp状态转移方程,有点错误。错误以为不能抢劫相邻的房子意味着抢的房子之间必须相隔一个房子,其实可以中间可以相隔多个房子不抢。
则dp转移方程为:即要不要抢当前的房子
dp[i] = max( dp[i-1] , dp[i-2] + nums[i] )
代码
初级
一个序列有N个数:A[1],A[2],…,A[N],求出最长非降子序列的长度。 (讲DP基本都会讲到的一个问题LIS:longest increasing subsequence)
正如上面我们讲的,面对这样一个问题,我们首先要定义一个“状态”来代表它的子问题, 并且找到它的解。注意,大部分情况下,某个状态只与它前面出现的状态有关, 而独立于后面的状态。
让我们沿用“入门”一节里那道简单题的思路来一步步找到“状态”和“状态转移方程”。 假如我们考虑求A[1],A[2],…,A[i]的最长非降子序列的长度,其中i<N, 那么上面的问题变成了原问题的一个子问题(问题规模变小了,你可以让i=1,2,3等来分析) 然后我们定义d(i),表示前i个数中以A[i]结尾的最长非降子序列的长度。OK, 对照“入门”中的简单题,你应该可以估计到这个d(i)就是我们要找的状态。 如果我们把d(1)到d(N)都计算出来,那么最终我们要找的答案就是这里面最大的那个。 状态找到了,下一步找出状态转移方程。
d(i) = max{1, d(j)+1},其中j<i,A[j]<=A[i]
用大白话解释就是,想要求d(i),就把i前面的各个子序列中, 最后一个数不大于A[i]的序列长度加1,然后取出最大的长度即为d(i)。 当然了,有可能i前面的各个子序列中最后一个数都大于A[i],那么d(i)=1, 即它自身成为一个长度为1的子序列。
62. Unique Paths
题目
的矩阵,从(0,0)位置走到(m,n)位置共有多少走法
思路
二维dp,dp[i][j]记录到达位置(i,j)共有的走法,dp[i][j]=dp[i-1][j]+dp[i][j-1].
代码
63. Unique Paths II
题目
同样是[m,n]矩阵,但是有1表示障碍,不能过,0为空白可以过去。
思路
dp[i][j]仍然是可能的走法数,但是在初始化时,如果当前是障碍,则dp[][]=0.否则依赖于前面一个。
代码
64. Minimum Path Sum
题目
从矩阵的左上角走到右下角,矩阵上元素值为代价,求最小代价
>
思路
完全捡苹果题目,需要注意的是创建dp数组时,len_row在外层,len_column在内层。
代码
120. Triangle
题目
Given a triangle, find the minimum path sum from top to bottom. Each step you may move to adjacent numbers on the row below.
>
思路
与捡苹果很相似,有两种想法,首先dp[i][j]表示到达需要的最少步数。那么状态转移方程有两种想法:
一种是:dp[i][j]出发有两种走法,dp[i+1][j]和dp[i+1][j+1],更新到达后的状态dp[i+1][j]和dp[i+1][j+1];
另一种是dp[i][j]有两种到达的方法,dp[i-1][j]和dp[i-1][j-1],更新dp[i][j]
但是觉得第一种方法比较容易,因为第二种要考虑边界
代码
213. House Robber II
题目
You are a professional robber planning to rob houses along a street. Each house has a certain amount of money stashed. All houses at this place are arranged in a circle. That means the first house is the neighbor of the last one. Meanwhile, adjacent houses have security system connected and it will automatically contact the police if two adjacent houses were broken into on the same night.
>
>
思路
房子排成了一个圆圈,则如果抢了第一家,就不能抢最后一家,因为首尾相连了,所以第一家和最后一家只能抢其中的一家,或者都不抢。则把数组分成两份,分别使用动态规划求解。
代码
279. Perfect Squares
题目
Given a positive integer n, find the least number of perfect square numbers (for example,
1, 4, 9, 16, ...) which sum to n.
思路
这道题就是找零钱。只是零钱的选取是有限的,而这边完美数是无限的,但是要小于n。故遍历零钱数组的操作,需要变成while循环,遍历每一个完美数。
dp[i]表示最少需要的数字凑成这个数,直到n。两层循环。
代码
300. Longest Increasing Subsequence
题目
Given an unsorted array of integers, find the length of longest increasing subsequence.
For example,
Given[10, 9, 2, 5, 3, 7, 101, 18],
The longest increasing subsequence is[2, 3, 7, 101], therefore the length is4. Note that there may be more than one LIS combination, it is only necessary for you to return the length.思路
如果动态规划,则时间复杂度是$O(n^2)$, 第一层循环来更新dp,第二个循环来遍历之前的数字且必须比当前小,不能等于。如样例,
[10,9,2,5,3,7,101,18],我们把原数组分成长度2,3,4,5,...,l的子数组求解最长上升,最终选择最佳的:
>
使用dp辅助数组记录每个元素与之前元素形成的最长上升。
>
代码
>
322. Coin Change
题目
换硬币,但是可能失败,即没有1元银币,导致凑不够。
>
>
思路
两层遍历,dp[i]表示凑够i元需要的最少银币数量。疑惑点是如何处理凑不够的情况,返回-1.事实上,只要有提供1元银币,一定可以凑够。那就判断dp[1]是否有更新。
代码
338. Counting Bits
题目
Given a non negative integer number num. For every numbers i in the range 0 ≤ i ≤ num calculate the number of 1’s in their binary representation and return them as an array.
>
思路
可以使用动态规划,时间复杂度是$O(n)$. 显然dp[i]表示数字里面含有的1的个数。但是状态转移如何表示?计算i的时候,如何利用dp[0]-dp[i-1]呢?利用➗2,即右移操作。一个数右移一位,变成较小的数字,失去的是最右的1或者0.则状态转移变成了
dp[i] = dp[i>>1] + i%2
代码
>
377. Combination Sum IV
题目
Given an integer array with all positive numbers and no duplicates, find the number of possible combinations that add up to a positive integer target.
>
Follow up: What if negative numbers are allowed in the given array? How does it change the problem? What limitation we need to add to the question to allow negative numbers?
思路
就是找银币了。但是不同于找硬币,其状态转移是dp[i] = dp[i-j] + 1;该问题的状态转移是dp[i] += dp[i-1]
代码
Integer Break(343)
题目
Given a positive integer n, break it into the sum of at least two positive integers and maximize the product of those integers. Return the maximum product you can get.
For example, given n = 2, return 1 (2 = 1 + 1); given n = 10, return 36 (10 = 3 + 3 + 4).
Note: You may assume that n is not less than 2 and not larger than 58.
思路
动态规划时间复杂度$O(n)$.难点在于状态转移方程,dp[i]表示i的因数的最大乘积。想到dp[i] = max( dp[i] , dp[j] (i-j) ),其实本质就是将i先分解成(【j】 【i-j】),但是j可以再分解,同样i-j也可以再分解,选择大的。
即max( j , dp[j] )* max(i-j ,dp[i-j])
故状态转移方程是:
dp[i] = max ( dp[i] , max( j , dp[j] )* max(i-j ,dp[i-j]) )
代码
Word Break(139)
题目
Given a non-empty string s and a dictionary wordDict containing a list of non-empty words, determine if s can be segmented into a space-separated sequence of one or more dictionary words.
123456789101112131415Example1:Input: s = "leetcode", wordDict = ["leet", "code"]Output: trueExplanation: Return true because "leetcode" can be segmented as "leet code".Example2:Input: s = "applepenapple", wordDict = ["apple", "pen"]Output: trueExplanation: Return true because "applepenapple" can be segmented as "apple pen apple". Note that you are allowed to reuse a dictionary word.Example3:Input: s = "catsandog", wordDict = ["cats", "dog", "sand", "and", "cat"]Output: false思路
$O(n^2)$的复杂度。
dp[i]表示子串$s[0,1…i-1]$能否由字典表示
dp[i] = true if dp[j]==true and s[j,j+1,…,i-1] is in dic.
代码
12345678910class Solution:def wordBreak(self, s, wordDict):dp = [False for i in range(len(s)+1)]dp[0] = Truefor i in range(1,len(s)+1):for j in range(i):if dp[j] and s[j:i] in wordDict:dp[i] = Truebreakreturn dp[-1]
中级
接下来,让我们来看看如何解决二维的DP问题。
平面上有N*M个格子,每个格子中放着一定数量的苹果。你从左上角的格子开始, 每一步只能向下走或是向右走,每次走到一个格子上就把格子里的苹果收集起来, 这样下去,你最多能收集到多少个苹果。
解这个问题与解其它的DP问题几乎没有什么两样。第一步找到问题的“状态”, 第二步找到“状态转移方程”,然后基本上问题就解决了。
首先,我们要找到这个问题中的“状态”是什么?我们必须注意到的一点是, 到达一个格子的方式最多只有两种:从左边来的(除了第一列)和从上边来的(除了第一行)。 因此为了求出到达当前格子后最多能收集到多少个苹果, 我们就要先去考察那些能到达当前这个格子的格子,到达它们最多能收集到多少个苹果。 (是不是有点绕,但这句话的本质其实是DP的关键:欲求问题的解,先要去求子问题的解)
经过上面的分析,很容易可以得出问题的状态和状态转移方程。 状态S[i][j]表示我们走到(i, j)这个格子时,最多能收集到多少个苹果。那么, 状态转移方程如下:
|
|
$S[i][j]$有两种计算方式:1.对于每一行,从左向右计算,然后从上到下逐行处理;2. 对于每一列,从上到下计算,然后从左向右逐列处理。 这样做的目的是为了在计算$S[i][j]$时,$S[i-1][j]$和$S[i][j-1]$都已经计算出来了。
Wiggle Subsequence
题目
A sequence of numbers is called a wiggle sequence if the differences between successive numbers strictly alternate between positive and negative. The first difference (if one exists) may be either positive or negative. A sequence with fewer than two elements is trivially a wiggle sequence.
For example,
[1,7,4,9,2,5]is a wiggle sequence because the differences (6,-3,5,-7,3) are alternately positive and negative. In contrast,[1,4,7,2,5]and[1,7,4,5,5]are not wiggle sequences, the first because its first two differences are positive and the second because its last difference is zero.Given a sequence of integers, return the length of the longest subsequence that is a wiggle sequence. A subsequence is obtained by deleting some number of elements (eventually, also zero) from the original sequence, leaving the remaining elements in their original order.
Examples:
12345678910Input: [1,7,4,9,2,5]Output: 6The entire sequence is a wiggle sequence.Input: [1,17,5,10,13,15,10,5,16,8]Output: 7There are several subsequences that achieve this length. One is [1,17,10,13,10,16,8].Input: [1,2,3,4,5,6,7,8,9]Output: 2思路
双重循环遍历,时间复杂度$O(n^2)$.
对于每一个元素,考虑与之前的元素构成最长的wiggle,有两种情况。一是当前元素是上升点,即当前元素值大于前面的,那么这样最长的长度是之前点作为下架点的长度+1;二是当前元素是下降点,即元素值小于前面的,那么长度是之前点作为上升点的长度+1。那么我们设置两个dp数组
dp_inc[]:如果与之前构成wiggle,当前元素是上升的点时,子序列的最长长度,状态更新
dp_inc[i] = max ( dp_inc[i] , dp_dec[j] + 1 ) if nums[i]>nums[j]
dp_dec[]:如果与之前构成wiggle,当前元素是下降的点时,子序列的最长长度,状态更新
dp_dec[i] = max ( dp_dec[i] , dp_inc[j] + 1 ) if nums[i] < nums[j]
代码
12345678910111213class Solution:def wiggleMaxLength(self, nums):l = len(nums)dp_inc, dp_dec = [1]*l,[1]*lfor i in range(1,l):target = nums[i]for j in range(i):cur = nums[j]if target>cur:dp_inc[i] = max(dp_inc[i],dp_dec[j]+1)elif target<cur:dp_dec[i] = max ( dp_dec[i] , dp_inc[j] + 1 )return max(dp_inc[-1],dp_dec[-1]) if l else 0
Ones and Zeroes(474)
题目
In the computer world, use restricted resource you have to generate maximum benefit is what we always want to pursue.
For now, suppose you are a dominator of m
0sand n1srespectively. On the other hand, there is an array with strings consisting of only0sand1s.Now your task is to find the maximum number of strings that you can form with given m
0sand n1s. Each0and1can be used at most once.12345678910111213Example1:Input: Array = {"10", "0001", "111001", "1", "0"}, m = 5, n = 3Output: 4Explanation: This are totally 4 strings can be formed by the using of 5 0s and 3 1s, which are “10,”0001”,”1”,”0”Example2:Input: Array = {"10", "0", "1"}, m = 1, n = 1Output: 2Explanation: You could form "10", but then you'd have nothing left. Better form "0" and "1".思路
代码
Maximal Square(221)
题目
Given a 2D binary matrix filled with 0’s and 1’s, find the largest square containing only 1’s and return its area.
>
思路
想不到用dp解决。
dp[i][j]表示以点[i][j]为右下角顶点的正方形的边长。为了构成全1正方形,该点必须是1,那么如何利用已经计算好的dp状态更新当前dp状态呢?即如何根据该点拓展正方形?与它上方,左方和左上方三个点有关。
当我们判断以某个点为正方形右下角时最大的正方形时,那它的上方,左方和左上方三个点也一定是某个正方形的右下角,否则该点为右下角的正方形最大就是它自己了。这是定性的判断,那具体的最大正方形边长呢?我们知道,该点为右下角的正方形的最大边长,最多比它的上方,左方和左上方为右下角的正方形的边长多1,最好的情况是是它的上方,左方和左上方为右下角的正方形的大小都一样的,这样加上该点就可以构成一个更大的正方形。但如果它的上方,左方和左上方为右下角的正方形的大小不一样,合起来就会缺了某个角落,这时候只能取那三个正方形中最小的正方形的边长加1了。假设
dp[i][j]表示以i,j为右下角的正方形的最大边长,则有
>
代码
96. Unique Binary Search Trees
题目
Given n, how many structurally unique BST’s (binary search trees) that store values 1 … n?
>
思路
不会想到用动态规划。但是知道可以dp,有大致的想法,我最初认为dp[i]表示数字1,2,…,i能形成的二叉树的数量。这样在状态转移的时候就有麻烦了。其实,与数字大小无关,即dp[i]也可以是9,10,11,…,i+9形成的二叉树,实际上,dp[i]状态表示的是i个有序上升点能形成的二叉树个数。这样问题就简单了。状态转移:
dp[i] += dp[j-1] * dp[i-j] 遍历j从1-i,表示以j为顶点形成的二叉树。
代码
91. Decode Ways
题目
A message containing letters from
A-Zis being encoded to numbers using the following mapping:
>
Given a non-empty string containing only digits, determine the total number of ways to decode it.
>
>
思路
可以想到用dp,但是一直纠结于dp的维数。
dp[i]表示1-i字符串的decode种类,那么状态转移方程呢?与具体的字符串有关。因为数字只能是一位或者两位,且一位的数字不能是0.那么如果当前的数字是0,那么不能以一位解码;否则可以以该种方式解码,则dp[i] += dp[i-1];如果i-1和i的两位数是合法的,即位于10和26之间,那么是可以以两位数解码,dp[i] += dp[i-2]
>
代码
368. Largest Divisible Subset
题目
Given a set of distinct positive integers, find the largest subset such that every pair (Si, Sj) of elements in this subset satisfies: Si % Sj = 0 or Sj % Si = 0.
If there are multiple solutions, return any subset is fine.
>
>
思路
题目是很复杂了,而且不会想到用dp,因为这边求解的是list,而非极值。看了网上代码,还是em。
首先不论返回的list,单纯看最大的可以是多大,因为取余有个性质,i>j>k, i % j = 0,j % k = 0, 那么i % k = 0.所以给了dp状态转移的思路,
dp[i]表示数字i以及i之前的数组能形成的最大子集,状态的更新只需要考虑i之前的数字能否取余为零
dp[i] = max( dp[i] , dp[j] +1 ) if i % j == 0
接下来难点就是如何记录结果list,当然我们可以设置一个二维数组来保存,一旦更新dp的时候,也要更新对应的list,即把i值加上上一个list中。但是我们可以把$O(n^2)$的空间复杂度变成$D(n)$, pre[i]记录i之前能取余且得到最大的子集的元素的下标。
>
代码
740. Delete and Earn
题目
Given an array
numsof integers, you can perform operations on the array.In each operation, you pick any
nums[i]and delete it to earnnums[i]points. After, you must delete every element equal tonums[i] - 1ornums[i] + 1.You start with 0 points. Return the maximum number of points you can earn by applying such operations.
思路
这道题本质上就是198题House Rober。
代码
718. Maximum Length of Repeated Subarray
题目
Given two integer arrays
AandB, return the maximum length of an subarray that appears in both arrays.
思路
经典动态规划。A[i]:表示A的子串0-i,B[j]:表示B的子串0-j
dp[i][j]:A的子串与B的子串最长重合,状态更新dp[i][j] = dp[i-1][j-1] + 1 if 两个子串的最后字符相同
代码
Minimum ASCII Delete Sum for Two Strings(712)
题目
Given two strings
s1, s2, find the lowest ASCII sum of deleted characters to make two strings equal. All elements of each string will have an ASCII value in[97, 122].
思路
这道题就是LCS (Longest Common Subsequence).
在LCS中,
d[i][j]表示s1.substring(0,i)和s2.substring(0,j)的LCS的长度, 那么
d[i][j]=d[i-1][j-1]+1 ifs1[i-1]==s2[j-1]
d[i][j]=max(d[i-1][j],d[i]]j-1) ifs1[i-1]!=s2[j-1]那么在本题背景下,
d[i][j]表示s1.substring(0,i)和s2.substring(0,j)删除若干个字符后相等的最小cost,那么
d[i][j]=d[i-1][j-1]+0 ifs1[i-1]==s2[j-1]
d[i][j]=min(d[i-1][j]+s1[i-1],d[i]]j-1+s2[j-1]) ifs1[i-1]!=s2[j-1]但是,这道题需要和718题的Maximum Length of Repeated Subarray作个比较,因为718题的状态转移方程是:
d[i][j]=d[i-1][j-1]+1 ifs1[i-1]==s2[j-1]
d[i][j]=0 ifs1[i-1]!=s2[j-1]差异在于 if
s1[i-1]!=s2[j-1],在718中,一旦不等,意味着连续的相等的子串已经消失,则当前的计算得重新开始,重点是“连续”而在本题以及LCS中,一旦不等,不必重新开始,因为没有要求“连续”,大不了跳过这个不等,则当前不等的计算就依赖于前面
代码
Knight Probability in Chessboard(688)
题目
On an
NxNchessboard, a knight starts at ther-th row andc-th column and attempts to make exactlyKmoves. The rows and columns are 0 indexed, so the top-left square is(0, 0), and the bottom-right square is(N-1, N-1).A chess knight has 8 possible moves it can make, as illustrated below. Each move is two squares in a cardinal direction, then one square in an orthogonal direction.
Each time the knight is to move, it chooses one of eight possible moves uniformly at random (even if the piece would go off the chessboard) and moves there.
The knight continues moving until it has made exactly
Kmoves or has moved off the chessboard. Return the probability that the knight remains on the board after it has stopped moving.思路
dp[i][j][k]:表示经过k次移动之后,knight到达位置[i,j]的所有可能方法数。那么状态转移有两种,一种是如果knight当前位置是[i][j],且当前是第k次移动,那么更新下一次从当前[i][j]位置可能到达的其他位置dp[i+x][j+y][k+1];另一种是当前位置是[i][j],且当前是第k次移动,那么上一次k-1移动是如何到达当前位置。本代码实现第一种方法,因为当前状态只与上一次状态有关,所以通过降维,使用
dp0[]和dp1[]表示k-1和k的可能性,’状态转移是:
dp1[i][j] += dp0[i+x][j+y]代码
Number of Longest Increasing Subsequence(673)
题目
Given an unsorted array of integers, find the number of longest increasing subsequence.
>
思路
dp[i]表示子串S[0] - S[i-1]的最长上升子串长度。动态转移方程是dp[i] = max (dp[i], dp[j] + 1), j 的范围是[0, i-1]。所以代码实现时,需要双重循环。但是,我们还需要记录一个构成最长子串的方式数。比如子串【1,2,4,2,3】,最长上升子串长度是3,但是有两种方式实现,【1,2,3】(2来自于index=1)和【1,2,3】[2来自于index=3]。
dp[i][2]:dp[i][0]表示子串S[0] - S[i-1]的最长上升子串长度,dp[i][1]第二维记录构成该最长子串的方式数
if dp[i][0]>dp[j][1] then dp[i][0] = dp[j][0] + 1, dp[i][1] = dp[i][1]
else if dp[i][0]==dp[j][1] then dp[i][1] += dp[i][1]
代码
>
2 Keys Keyboard
题目
Initially on a notepad only one character ‘A’ is present. You can perform two operations on this notepad for each step:
Copy All: You can copy all the characters present on the notepad (partial copy is not allowed).Paste: You can paste the characters which are copied last time.Given a number
n. You have to get exactlyn‘A’ on the notepad by performing the minimum number of steps permitted. Output the minimum number of steps to getn‘A’.
>
- 思路
代码
>
Out of Boundary Paths(576)
题目
There is an m by n grid with a ball. Given the start coordinate (i,j) of the ball, you can move the ball to adjacent cell or cross the grid boundary in four directions (up, down, left, right). However, you can at most move N times. Find out the number of paths to move the ball out of grid boundary. The answer may be very large, return it after mod 109 + 7.
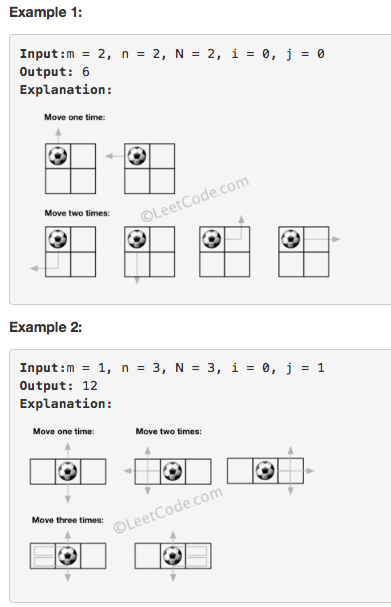
思路
这道题给了我们一个二维的数组,某个位置放个足球,每次可以在上下左右四个方向中任意移动一步,总共可以移动N步,问我们总共能有多少种移动方法能把足球移除边界,由于结果可能是个巨大的数,所以让我们对一个大数取余。那么我们知道对于这种结果很大的数如果用递归解法很容易爆栈,所以最好考虑使用DP来解。那么我们使用一个三维的DP数组,其中dp[k][i][j]表示总共走k步,从(i,j)位置走出边界的总路径数。那么我们来找递推式,对于dp[k][i][j],走k步出边界的总路径数等于其周围四个位置的走k-1步出边界的总路径数之和,如果周围某个位置已经出边界了,那么就直接加上1,否则就在dp数组中找出该值,这样整个更新下来,我们就能得出每一个位置走任意步数的出界路径数了,最后只要返回dp[N][i][j]就是所求结果了,参见代码如下.
代码
123456789101112class Solution:def findPaths(self, m, n, N, i, j):dp = [[[0 for _ in range(N+1)] for _ in range(n)] for _ in range(m)]##N+1是为了防止出现N=0情况。for k in range(1,N+1):for ii in range(m):for jj in range(n):v1 = 1 if ii==0 else dp[ii-1][jj][k-1]v2 = 1 if ii==m-1 else dp[ii+1][jj][k-1]v3 = 1 if jj==0 else dp[ii][jj-1][k-1]v4 = 1 if jj==n-1 else dp[ii][jj+1][k-1]dp[ii][jj][k] = (v1+v2+v3+v4)%1000000007return dp[i][j][N]
Longest Palindromic Subsequence(516)—for(Length)
题目
Given a string s, find the longest palindromic subsequence’s length in s. You may assume that the maximum length of s is 1000.
12345678Example1:Input:"bbbab" Output:4One possible longest palindromic subsequence is "bbbb".Example2:Input:"cbbd" Output:2One possible longest palindromic subsequence is "bb".思路
dp[i][j]表示字符串s[i…j]的最长回文串长度。
dp[i][j] = 1 表示单个单个字符s[i]就是一个回文串
dp[i][j] = dp[i+1][j-1] + 2 if s[i]==s[j], else
dp[i][j] = max (dp[i+1][j], dp[i][j-1])
代码
123456789101112131415161718class Solution:def longestPalindromeSubseq(self, s):""":type s: str:rtype: int"""l = len(s)dp = [[0 for _ in range(l)] for _ in range(l)]for i in range(l):dp[i][i] = 1for ll in range(1,l+1):for i in range(0,l-ll):j = i+llif s[i]==s[j]:dp[i][j] = dp[i+1][j-1] + 2else:dp[i][j] = dp[i+1][j] if dp[i+1][j] > dp[i][j-1] else dp[i][j-1]return dp[0][l-1]
Predict the Winner(486)—for(Length)
题目
Given an array of scores that are non-negative integers. Player 1 picks one of the numbers from either end of the array followed by the player 2 and then player 1 and so on. Each time a player picks a number, that number will not be available for the next player. This continues until all the scores have been chosen. The player with the maximum score wins.
Given an array of scores, predict whether player 1 is the winner. You can assume each player plays to maximize his score.
123456789101112131415Example1:Input: [1, 5, 2]Output: FalseExplanation: Initially, player 1 can choose between 1 and 2.If he chooses 2 (or 1), then player 2 can choose from 1 (or 2) and 5. If player 2 chooses 5, then player 1 will be left with 1 (or 2).So, final score of player 1 is 1 + 2 = 3, and player 2 is 5.Hence, player 1 will never be the winner and you need to return False.Example2:Input: [1, 5, 233, 7]Output: TrueExplanation: Player 1 first chooses 1. Then player 2 have to choose between 5 and 7. No matter which number player 2 choose, player 1 can choose 233.Finally, player 1 has more score (234) than player 2 (12), so you need to return True representing player1 can win.思路
dp[i][j]表示子串s[i…j]供选择时两个玩家间的总分数差,无论是玩家1还是玩家2,都希望最大化差异,那么状态转移就是:
dp[i][j] = max(nums[i] - dp[i+1][j] , nums[j] - dp[i][j-1])
代码
123456789101112131415class Solution:def PredictTheWinner(self, nums):""":type nums: List[int]:rtype: bool"""l = len(nums)dp = [[0 for _ in range(l)] for _ in range(l)]for i in range(l):dp[i][i] = nums[i]for dis in range(1,l): #the distance between index of i and jfor i in range(l-dis):j = i+disdp[i][j] = nums[i]-dp[i+1][j] if nums[i]-dp[i+1][j]>nums[j]-dp[i][j-1] else nums[j]-dp[i][j-1]return dp[0][l-1]>=0
Target Sum(494)
题目
You are given a list of non-negative integers, a1, a2, …, an, and a target, S. Now you have 2 symbols
+and-. For each integer, you should choose one from+and-as its new symbol.Find out how many ways to assign symbols to make sum of integers equal to target S.
1234567891011Input: nums is [1, 1, 1, 1, 1], S is 3.Output: 5Explanation:-1+1+1+1+1 = 3+1-1+1+1+1 = 3+1+1-1+1+1 = 3+1+1+1-1+1 = 3+1+1+1+1-1 = 3There are 5 ways to assign symbols to make the sum of nums be target 3.思路
解法1:
经典动态规划。首先,将问题简单化,只考虑通过组合number,是否能组成得到target。
$V_i$表示使用num[0],num[1],…,nums[i]个数字组成可以得到的所有可能数字
那么$V_0={0}$,$V_i=\{V_{i-1}+num[i]\}\cup{\{V_{i-1}-num[i]\}}$
则判断$target\in{V_n}$
现在考虑数字组合得到target的方法数目,使用dp[i][j]来记录num[0],num[1],…,num[i-1]个数字组成得到sum=j的不同方式数。那么状态转移就是:
dp[i][j] = dp[i-1][j+num[i]] + dp[i-1][j-num[i]]
令num[0], num[1], num[2],…的和为TSUM,而所有可能的sum值,即dp第二维的长度是2*TSUM+1,即{-TSUM, -TSUM+1,…-1,0,1,…,TSUM-1,TSUM}。
初始化:dp[-1][0] = 1 组合使和0有一种方式,即什么都不操作。而sum=0的index是TSUM即dp[-1][TSUM]=1
解法2:
$P$ 表示集合,其中数字的符号只有“+”;$N$ 表示负数集合
那么$P\cup{N}=\{a_1,a_2,…,a_n\}$, $P\cap{N}=\empty$
那么问题就变成寻找集合$P$和$Q$,使$sum(P)-sum(N)=target$.
两边同时加上$sum(P)+sum(N)$
$sum(P)-sum(N)+sum(P)+sum(N)=target+sum(P)+sum(N)$
化简得到,$2*sum(P)=sum(a_1,a_2,…,a_n)+target$
即$sum(P)=\frac{sum(a_1,a_2,…,a_n)+target}{2}$
这样问题就变成了0-1背包问题,从$a_1,a_2,..,a_n$中凑成价值为$sum(P)$的方案。
代码
1234567891011121314151617181920212223242526272829303132333435363738####解法1class Solution:def findTargetSumWays(self, nums, S):""":type nums: List[int]:type S: int:rtype: int"""sums = sum(nums)if sums<S:return 0l = len(nums)dp = [[0 for _ in range(2*sums+1)] for _ in range(l+1)]dp[0][sums] = 1for i in range(l):for j in range(nums[i],2*sums+1-nums[i]):if (dp[i][j]!=0): #表示前i-1个数字可以组成(j-tsum),那么通过吸收+num[i],dp[i][j]可以更新 dp[i+1][j+nums[i]] 和 dp[i+1][j-nums[i]]dp[i+1][j+nums[i]] += dp[i][j]dp[i+1][j-nums[i]] += dp[i][j]return dp[-1][S+sums]####解法2:class Solution:def findTargetSumWays(self, nums, S):""":type nums: List[int]:type S: int:rtype: int"""sumA = sum(nums)if (sumA + S) % 2 == 1 or sumA < abs(S): return 0target = (sumA+S)//2dp = [0 for _ in range(target+1)]dp[0] = 1for num in nums:for j in range(target,-1,-1):if j>=num:dp[j] += dp[j-num]return dp[target]
高级
801. Minimum Swaps To Make Sequences Increasing
题目
We have two integer sequences
AandBof the same non-zero length.We are allowed to swap elements
A[i]andB[i]. Note that both elements are in the same index position in their respective sequences.At the end of some number of swaps,
AandBare both strictly increasing. (A sequence is strictly increasing if and only ifA[0] < A[1] < A[2] < ... < A[A.length - 1].)Given A and B, return the minimum number of swaps to make both sequences strictly increasing. It is guaranteed that the given input always makes it possible.
>
思路
文字 https://blog.csdn.net/magicbean2/article/details/79826617
这道题实在是太难了,不过看图片还是可以稍微有点顺畅。
代码
787. Cheapest Flights Within K Stops
题目
There are
ncities connected bymflights. Each fight starts from cityuand arrives atvwith a pricew.Now given all the cities and fights, together with starting city
srcand the destinationdst, your task is to find the cheapest price fromsrctodstwith up tokstops. If there is no such route, output-1.
>
>
思路
dp[i][j]表示从src城市出发,经过i站,到达城市j
状态转移:
dp[i][j] = min ( dp[i][j] , dp[i-1][mid]+cost[mid][j] )
代码
790. Domino and Tromino Tiling
题目
We have two types of tiles: a 2x1 domino shape, and an “L” tromino shape. These shapes may be rotated.
>
Given N, how many ways are there to tile a 2 x N board? Return your answer modulo 10^9 + 7.
(In a tiling, every square must be covered by a tile. Two tilings are different if and only if there are two 4-directionally adjacent cells on the board such that exactly one of the tilings has both squares occupied by a tile.)
>
思路
图片:http://zxi.mytechroad.com/blog/dynamic-programming/leetcode-790-domino-and-tromino-tiling/
>
代码
5. Longest Palindromic Substring
题目
Given a string s, find the longest palindromic substring in s. You may assume that the maximum length of s is 1000.
>
>
思路
这道题的难点在于,使用下标i和j来表示substring,i和j具体应该如何变化。实际上,i和j分别表示子串的结束字符和开头字符,如果s[i] != s[j],那么dp[i][j]=false; 否则查看j+1 至 i-1之间是否回文。
>
代码
764. Largest Plus Sign
题目
In a 2D
gridfrom (0, 0) to (N-1, N-1), every cell contains a1, except those cells in the given listmineswhich are0. What is the largest axis-aligned plus sign of1s contained in the grid? Return the order of the plus sign. If there is none, return 0.An “axis-aligned plus sign of 1s of order k“ has some center
grid[x][y] = 1along with 4 arms of lengthk-1going up, down, left, and right, and made of1s. This is demonstrated in the diagrams below. Note that there could be0s or1s beyond the arms of the plus sign, only the relevant area of the plus sign is checked for 1s.Examples of Axis-Aligned Plus Signs of Order k:
>
Example1
>
Example2
>
Example3
>
思路
>
代码
>
