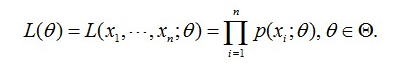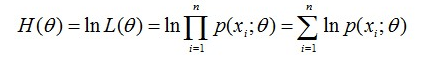极大似然估计，是参数估计的方法之一。其基本思想是已知样本符合某种概率分布，但是分布的参数未知，于是通过采样的随机样本估计参数。其基本步骤是：

求出似然函数：该样本集的概率，即每个样本出现的概率连积
对似然函数取对数：将连乘变连加
求导：使对数似然函数取最大值的参数便是结果
求解方程：得到的参数即为所求。

期望最大算法，是一种从不完全数据或有数据丢失的数据集（存在隐含变量）中求解概率模型参数的最大似然估计方法。在每一次的迭代过程中，主要分为两步：即求期望(Expectation)步骤和最大化(Maximization)步骤。

极大似然估计(Maximum Likelihood)

问题

假设需要调查学校的男生身高分布，于是采用采样的方法在校园里随机的访问了100个男生。于是统计抽样得到了100个男生的身高，假设他们的身高服从正态分布，但是这个分布的均值$\mu$和方差$\delta^2$是未知的，即这两个参数是需要估计的，记作$\theta=[\mu,\delta]$。

用数学的语言来说就是：在学校的男生中，独立地按照概率密度函数$p(x|\theta)$抽样了100个人的身高，组成样本集$X$,我们想通过样本集$X$来估计未知参数$\theta$。

分析

由于每个样本都是独立地从$p(x|\theta)$中抽取的，换句话说这100个男生中的任何一个，都是随机抽取的，从我的角度来看这些男生之间是没有关系的。那么，我从学校那么多男生中为什么就恰好抽到了这100个人呢？抽到这100个人的概率是多少呢？因为这些男生（的身高）是服从同一个高斯分布$p(x|\theta)$的。那么我抽到男生A（的身高）的概率是$p(x_A|\theta)$，抽到男生B的概率是$p(x_B|\theta)$，那因为他们是独立的，所以很明显，我同时抽到男生A和男生B的概率是$p(x_A|\theta)\times{p(x_B|\theta)}$，同理，我同时抽到这100个男生的概率就是他们各自概率的乘积了。用数学家的口吻说就是从分布是$p(x|\theta)$的总体样本中抽取到这100个样本的概率，也就是样本集X中各个样本的联合概率，用下式表示：

这个概率反映了，在概率密度函数的参数是$theta$时，得到X这组样本的概率。因为这里X是已知的，也就是说我抽取到的这100个人的身高可以测出来，则每一种身高在该100个样本中可以计算$p(x_i;\theta)=\frac{身高为x_i的人数$}{100}$。而$\theta$是未知了，则上面这个公式只有θ是未知数，所以它是$\theta$的函数。这个函数放映的是在不同的参数$\theta$取值下，取得当前这个样本集的可能性，因此称为参数$\theta$相对于样本集X的似然函数（likehood function）。记为$L(\theta)$。

参数估计

似然函数思想：抽取的样本的概率最大

下课了，一群男女同学分别去厕所了。然后，你想知道课间是男生上厕所的人多还是女生上厕所的人比较多，然后你就跑去蹲在男厕和女厕的门口。蹲了五分钟，你跑过来告诉我，课间女生上厕所的人比较多。我问你是怎么知道的。你说：“5分钟了，出来的是女生，女生啊，那么女生出来的概率肯定是最大的了，或者说比男生要大，那么女厕所的人肯定比男厕所的人多”。看到了没，你已经运用最大似然估计了。你通过观察到女生先出来，那么什么情况下，女生会先出来呢？肯定是女生出来的概率最大的时候了，那什么时候女生出来的概率最大啊，那肯定是女厕所比男厕所多人的时候了，这个就是你估计到的参数了。

回到男生身高那个例子。在学校那么男生中，我一抽就抽到这100个男生（表示身高），而不是其他人，那是不是表示在整个学校中，这100个人（的身高）出现的概率最大啊。那么这个概率怎么表示？就是上面那个似然函数$L(\theta)$。所以，我们就只需要找到一个参数θ，其对应的似然函数$L(\theta)$最大，也就是说抽到这100个男生（的身高）概率最大。这个叫做$\theta$的最大似然估计量，记为：
$\hat{\theta}=arg maxL(\theta)$
可以看到$L(\theta)$是连乘的，所以为了便于分析，还可以定义对数似然函数，将其变成连加的：

这样使似然函数取得最大值的$\theta$便是我们的估计。这里就回到了求最值的问题了。怎么求一个函数的最值？当然是求导，然后让导数为0，那么解这个方程得到的$\theta$就是了（当然，前提是函数$L(\theta)$连续可微）。那如果θ是包含多个参数的向量那怎么处理啊？当然是求$L(\theta)$对所有参数的偏导数，也就是梯度了，那么n个未知的参数，就有n个方程，方程组的解就是似然函数的极值点了，当然就得到这n个参数了。

例子

SciPy.minimize

题目

采用geyser 数据，该数据采集自美国黄石公园内的一个名叫 Old Faithful 的喷泉。“waiting”就是喷泉两次喷发的间隔时间，“duration”当然就是指每次喷发的持续时间。在这里，我们只用到 “waiting” 数据。
1

2

3

4

5

6

7

waiting duration

1 80 4.0166667

2 71 2.1500000

3 57 4.0000000

4 80 4.0000000

5 75 4.0000000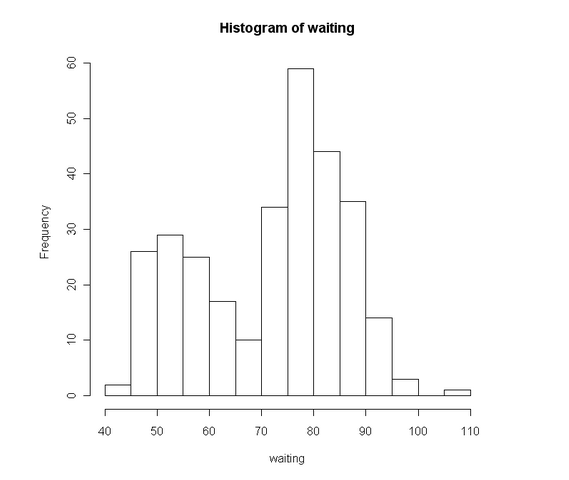

......

代码

import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats #获取正态分布
from scipy.optimize import minimize #目标优化

#####数据存储于.txt文件中
data = np.loadtxt('data')
values = []
for i in data:
    values.append(i[2])
values = np.array(values)

#####定义极大似然函数
def objective_func(params):#优化函数，总共优化5个参数
    prob = params[0]
    mu1 = params[1]
    sigma1 = params[2]
    mu2 = params[3]
    sigma2 = params[4]
    norm_dis1 = stats.norm.pdf(values,loc=mu1,scale=sigma1) #将x轴数据输入，输出该样本的正态分布的概率密度
    norm_dis2 = stats.norm.pdf(values,loc=mu2,scale=sigma2)
    f = prob*norm_dis1+(1-prob)*norm_dis2
    L = np.sum(np.log(f))
    return -L #minimize函数求解最小值，但是我们要最大化，所以加一个“-”

#####求解
param = np.array([0.5,50,10,80,10]) #参数初始化,根据数据直方分布图猜测
results = minimize(objective_func, param, method='nelder-mead')
paramss = results.x #[0.36088303 54.61479245  5.87121392 80.09109663  5.86777145]
prob = paramss[0]
mu1 = paramss[1]
sigma1 = paramss[2]
mu2 = paramss[3]
sigma2 = paramss[4]

#####数据可视化
x = np.linspace(40,120,100)
f = prob*stats.norm.pdf(x,loc=mu1,scale=sigma1) + (1-prob)*stats.norm.pdf(x,loc=mu2,scale=sigma2)
plt.plot(x,f,color='r') #将估计的参数函数代入原密度函数。
plt.show()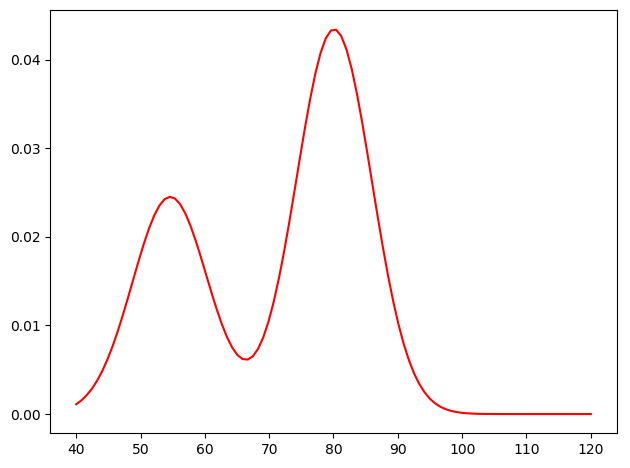

Screen Shot 2018-06-03 at 8.44.22 PM

期望最大算法()

问题

回到上面那个身高分布估计的问题。现在，通过抽取得到的那100个男生的身高和已知的其身高服从高斯分布，我们通过最大化其似然函数，就可以得到了对应高斯分布的参数$\theta=[\mu,\sigma]^T$了。那么，对于我们学校的女生的身高分布也可以用同样的方法得到了。

如果对学生抽样时，男生和女生混合在一起，200个人（的身高）里面随便给我指一个人（的身高），我都无法确定这个人（的身高）是男生（的身高）还是女生（的身高）。也就是说你不知道抽取的那200个人里面的每一个人到底是从男生的那个身高分布里面抽取的，还是女生的那个身高分布抽取的。用数学的语言就是，抽取得到的每个样本都不知道是从哪个分布抽取的。这个时候，对于每一个样本或者你抽取到的人，就有两个东西需要猜测或者估计的了，一是这个人是男的还是女的？二是男生和女生对应的身高的高斯分布的参数是多少？只有当我们知道了哪些人属于同一个高斯分布的时候，我们才能够对这个分布的参数作出靠谱的预测，例如刚开始的最大似然所说的，但现在两种高斯分布的人混在一块了，我们又不知道哪些人属于第一个高斯分布，哪些属于第二个，所以就没法估计这两个分布的参数。反过来，只有当我们对这两个分布的参数作出了准确的估计的时候，才能知道到底哪些人属于第一个分布，那些人属于第二个分布。

分析

EM的意思是“Expectation Maximization”，在我们上面这个问题里面，我们是先随便猜一下男生（身高）的正态分布的参数：如均值和方差是多少。例如男生的均值是1米7，方差是0.1米（当然了，刚开始肯定没那么准），然后计算出每个人更可能属于第一个还是第二个正态分布中的（例如，这个人的身高是1米8，那很明显，他最大可能属于男生的那个分布），这个是属于Expectation一步。有了每个人的归属，或者说我们已经大概地按上面的方法将这200个人分为男生和女生两部分，我们就可以根据之前说的最大似然那样，通过这些被大概分为男生的n个人来重新估计第一个分布的参数，女生的那个分布同样方法重新估计。这个是Maximization。然后，当我们更新了这两个分布的时候，每一个属于这两个分布的概率又变了，那么我们就再需要调整E步……如此往复，直到参数基本不再发生变化为止。

这里把每个人（样本）的完整描述看做是三元组yi={xi,zi1,zi2}，其中，xi是第i个样本的观测值，也就是对应的这个人的身高，是可以观测到的值。zi1和zi2表示男生和女生这两个高斯分布中哪个被用来产生值xi，就是说这两个值标记这个人到底是男生还是女生（的身高分布产生的）。这两个值我们是不知道的，是隐含变量。确切的说，zij在xi由第j个高斯分布产生时值为1，否则为0。例如一个样本的观测值为1.8，然后他来自男生的那个高斯分布，那么我们可以将这个样本表示为{1.8, 1, 0}。如果zi1和zi2的值已知，也就是说每个人我已经标记为男生或者女生了，那么我们就可以利用上面说的最大似然算法来估计他们各自高斯分布的参数。但是它们未知，因此我们只能用EM算法。

EM算法推导

假设我们知道了样本$X=\{x_1,x_2,…,x_n\}$的分布，比如正态分布，那么我们需要估计的参数就是均值$\mu$和方差$\sigma^2$，即：
$\mu=\frac{x_1+x_2+...+x_n}{n}\\ \sigma^2=\frac{(x_1-\mu)^2+(x_2-\mu)^2+...+(x_n-\mu)^2}{n}$
这样我们就可以估计样本分布参数了。

但是对于给定的样本$X=\{x_1,x_2,…,x_n\}$,假设它们来自于两个正态分布$N_1(\mu_1,\sigma_1^2)$和$N_2(\mu_2,\sigma_2^2)$，但是我们不知道每一个样本$x_i$具体来自于哪一个分布，所以我们的额外需要估计的一个参数$\pi$，即每一个样本点来自于分布1的概率向量，那么每一个样本点来自于样本2的概率就是$1-\pi$。

假设我们知道了两个分布，即两个正态分布的参数已知，那么对于每一个样本$x_i$，我们假设这个样本来自于$N_1$，那么我们可以计算出该样本的概率$\pi(i)=P_{N_1}(x_i)$；同理，我们也可以计算出该样本属于$N_2$的概率$P_{N_2}(x_i)$。这样，直觉上，概率越大，样本点越可能属于对应的那个分布。对所有的样本点进行这样的概率比较，我们就可以将样本点分成两类，一个是更可能属于分布1的样本点$X_{N_1}$，一个是更可能属于分布2的样本点$X_{N_2}$。这样，我们就可以使用 $X_{N_1}$ 中的点去更新$N_1$中的参数：
$\mu_1=\frac{\pi(1)x_1+\pi(2)x_2+...+\pi(n)x_n}{\pi(1)+\pi(2)+...+\pi(n)}\\ \sigma_1^2=\frac{\pi(1)(x_1-\mu)^2+\pi(2)(x_2-\mu)^2+...+\pi(n)(x_n-\mu)^2}{\pi(1)+\pi(2)+...+\pi(n)}$
同理，对于分布2的参数估计：
$\mu_2=\frac{(1-pi(1))x_1+(1-\pi(2))x_2+...+(1-\pi(n))x_n}{(1-\pi(1))+(1-\pi(2))+...+(1-\pi(n))}\\ \sigma_2^2=\frac{(1-\pi(1))(x_1-\mu)^2+(1-\pi(2))(x_2-\mu)^2+...+(1-\pi(n))(x_n-\mu)^2}{(1-\pi(1))+(1-\pi(2))+...+(1-\pi(n))}$

例子1：双硬币问题

问题

假设有两枚硬币A、B，以相同的概率随机选择一个硬币，进行如下的抛硬币实验：共做5次实验，每次实验独立的抛十次，结果如图中a所示，例如某次实验产生了H、T、T、T、H、H、T、H、T、H，H代表正面朝上。假设试验数据记录员可能是实习生，业务不一定熟悉，造成a和b两种情况 a表示实习生记录了详细的试验数据，我们可以观测到试验数据中每次选择的是A还是B b表示实习生忘了记录每次试验选择的是A还是B，我们无法观测实验数据中选择的硬币是哪个问在两种情况下分别如何估计两个硬币正面出现的概率？

对于已知是A硬币还是B硬币抛出的结果的时候，可以直接采用概率的求法来进行求解。对于含有隐变量的情况，也就是不知道到底是A硬币抛出的结果还是B硬币抛出的结果的时候，就需要采用EM算法进行求解了。如下图：
分析

对于已知样本来源，那么我们需要估计的参数，对于硬币A，其正面概率$\theta_A$，那么其反面概率即$1-\theta_A$；对于硬币B，其正面概率$\theta_B$，那么其反面概率即$1-\theta_B$；那么$\theta_A=\frac{正面样本数}{硬币A的样本数}=\frac{24}{24+6}=0.8$

那么对于不知道样本来源，我们先假设$\theta_A=0.6，\theta_B=0.5$,这样我们需要去估计每一个样本来自于硬币A的概率分布$\pi$，即由贝叶斯法则：
$\pi(A|i)=\frac{p(A)p(i|A)}{p(i)}$
比如对于第一行的第一个硬币结果是H，那么$p(i|A)=0.6$，即硬币A产生正面的概率是0.6；$p(A)=\frac{1}{2}$，即选择硬币A的概率是0.5；$p(i)=p(A)p(i|A)+p(B)p(i|B)$，即硬币A和B均可以产生正面。

那么$\pi(1)=0.55$，即如果是正面向上的样本点，它有0.55可能性来自于样本A。同理可以计算出反面向上的样本点来自于A的概率是0.44，则所有样本点的$\pi=(H,T,T,T,H,…,H,T,H)=(0.55,0.44,0.44,0.44,0.55,…,0.55,0.44,0.55)$

那么更新$\theta_A,\theta_B$:
$\theta_A=\frac{正面次数}{总次数}=\frac{0.55*(5+9+8+4+7)}{0.55*33+0.44*17}=0.71\\ \theta_B=\frac{(1-0.55)*(33)}{(1-0.55)*33+(1-0.44)*17}=0.61$
代码

例子2：混合高斯模型

问题

假设我们有一观测样本$X=\{X_1,X_2,..,X_n\}$, 已知$X$ 是由$k$ 个高斯分布均匀混合而成，这$k$个高斯分布的均值不同，但是有相同的方差。简单起见，$k=2$。
思路
代码