Python-SciPy

Posted on | In

Scipy基于Numpy，提供了大量科学算法，它的不同子模块相应于不同的应用，本文参考了1 2

  1. 文件IO（scipy.io）：数据输入输出
  2. 特殊函数（scipy.special）：特殊函数是先验函数，常用的有伽马函数scipy.special.gamma()
  3. 线性代数运算（scipy.linalg）
  4. 快速傅里叶变化（scipy.fftpack）
  5. 优化和拟合（scipy.optimize）：提供了函数最小值(标量或多维)、曲线拟合和寻找等式的根的有用算法。
  6. 统计和随机数（scipy.stats）
  7. 数值积分（scipy.integrate Fusy）

模块导入的标准方式是：

1


2


import numpy as np


from scipy import io #其他模块类似

文件输入/输出：scipy.io

导入和保存matlab文件

1


2


3


4


5


6


from scipy import io as spio


import numpy as np




a = np.ones((3,3)) #3*3的全1矩阵


spio.savemat('file.mat',{'a':a}) #以字典形式保存


data = spio.loadmat('file.mat',struct_as_record=True)

图片读取

1


2


3


4


import numpy as np


from scipy import misc




x = misc.imread("scipy.png")

txt/csv

1


2


3


4


5


6


7


8


numpy.loadtxt()


numpy.savetxt()


numpy.genfromtxt() #智能导入文本


numpy.recfromcsv() #智能导入csv文件




#高速，有效率但numpy特有的二进制格式：


numpy.save() 


numpy.load()

线性代数运算：scipy.linalg

行列式

1


2


3


4


5


import numpy as np


from scipy import linalg




x = np.array([[1,2],[3,4]])


re = linalg.det(x) #-2.0

逆矩阵

1


2


3


4


5


import numpy as np


from scipy import linalg




x = np.array([[1,2],[3,4]])


re = linalg.inv(x)

奇异值分解SVD

1


2


3


4


5


6


7


8


9


10


import numpy as np


from scipy import linalg




x = np.array([[1,2],[3,4]])


uarr,spec,vharr = linalg.svd(x)




###原始矩阵可以由svd的输出用np.dot点乘重新组合得到


sarr = np.diag(spec)


svd_mat = uarr.dot(sarr).dot(vharr)


re = np.allclose(svd_mat,x) #True

快速傅里叶变换：scipy.fftpack

优化和拟合：scipy.optimize

标量函数最小值

1


2


3


4


5


6


7


8


9


import numpy as np


from scipy import optimize


import matplotlib.pyplot as plt




def f(x):


    return x**2 + 10*np.sin(x)


x = np.arange(-10,10,0.1)


plt.plot(x,f(x))


plt.show()

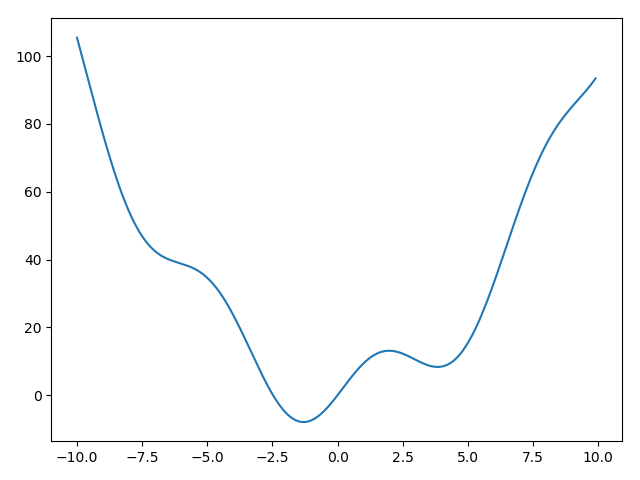
image-20180608001714621

1


2


3


4


5


6


7


8


9


10


####从上面图像可以看出x在-1.3附近有个全局最小值，在3.8附近有个局部最小


####从初始点使用梯度下降法求解，BFGS算法


re = optimize.fmin_bfgs(f,0) ##必须定义成函数


print(re)


#Optimization terminated successfully.


#Current function value: -7.945823


#Iterations: 5


#Function evaluations: 18


#Gradient evaluations: 6


#[-1.30644012]


1


2


3


4


5


6


7


8


9


10


11


12


13


14


15


16


#这个方法一个可能的问题在于，如果函数有局部最小值，算法会因初始点不同找到这些局部最小而不是全局最小:


re = optimize.fmin_bfgs(f,3) #[3.83746709]


#如果我们不知道全局最小值的邻近值来选定初始点，我们需要借助于耗费资源些的全局优化。为了找到全局最小点，最简单的算法是蛮力算法^2，该算法求出给定格点的每个函数值。


import numpy as np


from scipy import optimize


import matplotlib.pyplot as plt




def f(x):


    return x**2 + 10*np.sin(x)


x = np.arange(-10,10,0.1)




grid = (-10,10,0.1)


re = optimize.brute(f,(grid,)) ##[-1.30641113]




##为了找到局部最小，我们把变量限制在(0, 10)之间，使用scipy.optimize.fminbound():


re_local = optimize.fminbound(f,0,10) ##3.8374671194983834

标量函数的根

1


2


3


4


5


6


7


8


9


10


11


12


13


14


15


#为了寻找根，例如令f(x)=0的点，对以上的用来示例的函数f我们可以使用scipy.optimize.fsolve()


import numpy as np


from scipy import optimize


import matplotlib.pyplot as plt




def f(x):


    return x**2 + 10*np.sin(x)


x = np.arange(-10,10,0.1)




root = optimize.fsolve(f,1)#初始猜测是1


print(root) #[0.]




#注意仅仅一个根被找到。检查f的图像在-2.5附近有第二个根。我们可以通过调整我们的初始猜测找到这一确切值


root = optimize.fsolve(f,-2.5)


print(root)#[-2.47948183]

曲线拟合

1


2


3


4


5


6


7


8


9


10


11


12


13


14


15


16


17


import numpy as np


from scipy import optimize


import matplotlib.pyplot as plt




def f(x):


    return x**2 + 10*np.sin(x)


xdata = np.linspace(-10,10,num=20)


#得到污染的数据


ydata = f(xdata) + np.random.randn(xdata.size)


#我们知道xdata-ydata大致服从y=x^2 + sin(x),但是噪声的引入而又偏差，我们需要拟合找出系数a和b，即y=a*x^2 + b*sin(x)




def f2(x,a,b):


    return a*x**2+b*np.sin(x)


guess = [2,2]


params, params_covariance = optimize.curve_fit(f2,xdata,ydata,guess)


# params = [0.98996991 9.87613168]


# params_covariance = [[1.23238891e-05 1.30651701e-11] [1.30651701e-11 6.29408152e-02]]

统计和随机数： scipy.stats

直方图和概率密度函数

1


2


3


4


5


6


7


8


9


10


11


12


13


14


15


16


#给定一个随机过程的观察值，它们的直方图是随机过程的pdf(概率密度函数)的估计器


import numpy as np


from scipy import stats


import matplotlib.pyplot as plt




a = np.random.normal(size=1000)


bins = np.arange(-4,5) # bins=[-4, -3, -2, -1,  0,  1,  2,  3,  4]




histogram = np.histogram(a,bins=bins,normed=True)[0]


bins = 0.5*(bins[1:]+bins[:-1]) #bins=[-3.5, -2.5, -1.5, -0.5,  0.5,  1.5,  2.5,  3.5]




b = stats.norm.pdf(bins)




plt.plot(bins,histogram,color='g')


plt.plot(bins,b,color='b')


plt.show()

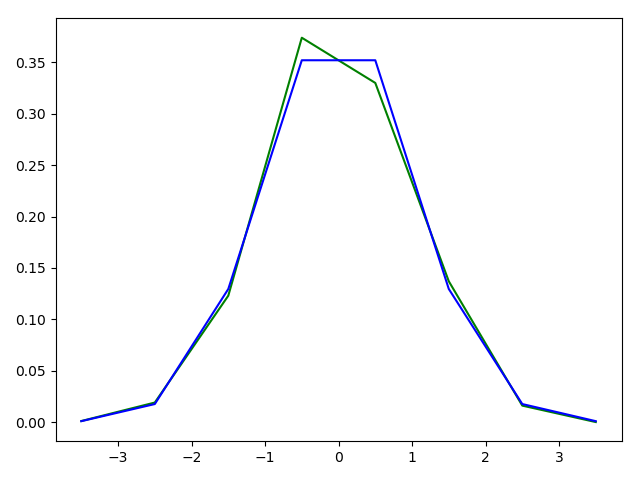
image-20180608005630507

1


2


#如果我们知道随机过程属于给定的随机过程族，比如正态过程。我们可以对观测值进行最大似然拟合来估计基本分布参数。这里我们对观测值拟合一个正态过程：


loc,std = stats.norm.fit(a) #loc= 0.007411672576925874 std= 1.005072454096087

百分位

1


2


3


4


5


6


7


8


9


#中位数,又叫作50百分位点，因为有50%的观测值在它之下,是来观测值之下一半之上一半的值。


import numpy as np


from scipy import stats


import matplotlib.pyplot as plt




a = np.random.normal(size=1000)




med = np.median(a)


med = stats.scoreatpercentile(a,50) #百分位是CDF的一个估计器

数值积分：scipy.integrate Fusy

1


2


3


4


5


import numpy as np


from scipy.integrate import quad




re,err = quad(np.sin,0,np.pi/2)


#re=0.9999999999999999, err=1.1102230246251564e-14

上述计算$\int_{0}^{\frac{\pi}{2}}sin(x)dx=1$