Python - Sklearn

Posted on | In

本文参考了1

通用学习模式

1


2


3


4


5


6


7


8


9


10


11


12


13


import numpy as np


from sklearn import datasets


from sklearn.model_selection import train_test_split


from sklearn.neighbors import KNeighborsClassifier


iris = datasets.load_iris()


iris_x = iris.data


iris_y = iris.target


# print(iris_x[:2,:]) #输出前面两个样本


# print(iris_y[2])


x_train,x_test,y_train,y_test= train_test_split(iris_x,iris_y,test_size=0.3)


knn = KNeighborsClassifier()


knn.fit(x_train,y_train)


result = knn.predict(x_train)

Sklearn中数据集

sklearn的[数据集] [官方说明]

Screen Shot 2018-06-28 at 9.34.12 AM

生成样本数据，按照函数的形式，输入 sample，feature，target 的个数等等

1


sklearn.datasets.make_regression(n_samples=100, n_features=100, n_informative=10, n_targets=1, bias=0.0, effective_rank=None, tail_strength=0.5, noise=0.0, shuffle=True, coef=False, random_state=None)[source]

Example: 房价预测

1


2


3


4


5


6


7


8


9


10


11


12


13


14


15


16


from sklearn import datasets


from sklearn.linear_model import LinearRegression


import matplotlib.pyplot as plt


#数据导入


loaded_data = datasets.load_boston()


data_x = loaded_data.data


data_y = loaded_data.target


#定义模型 and 训练模型


model = LinearRegression()


model.fit(data_x,data_y)


#预测


result = model.predict(data_x[:4,:])#预测前四个样本


print(result)


# [30.00821269 25.0298606  30.5702317  28.60814055]


print(data_y[:4]) # 打印真实值，作为对比，可以看到是有些误差的。


# [24.  21.6 34.7 33.4]

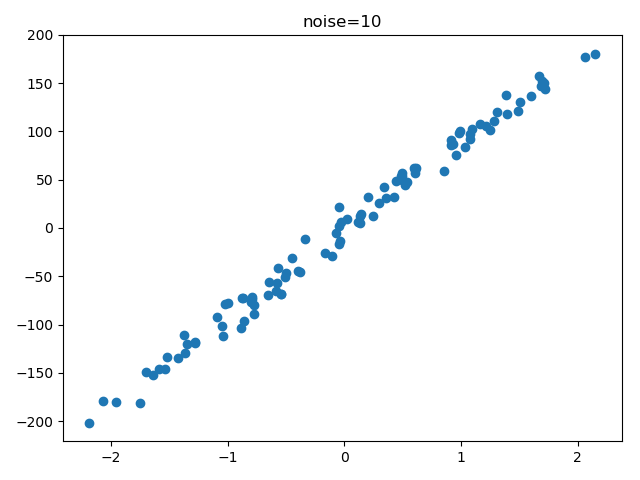
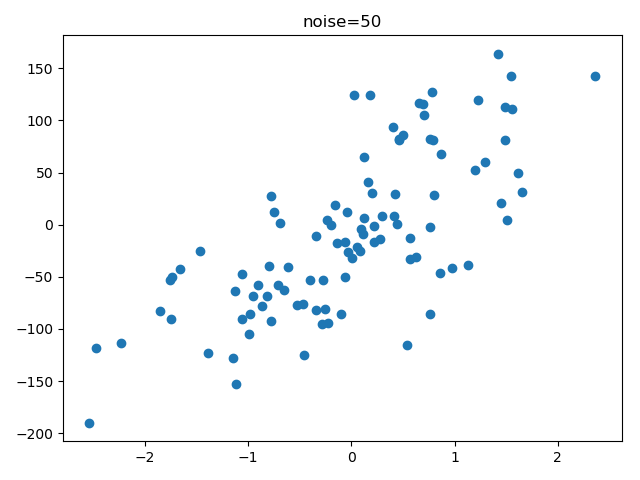
Example：生成样本数据

1


2


3


4


5


6


7


8


9


10


11


from sklearn import datasets


from sklearn.linear_model import LinearRegression


import matplotlib.pyplot as plt


# 建立 100 个 sample，有一个 feature，和一个 target的样本数据集


x,y = datasets.make_regression(n_samples=100,n_features=1,n_targets=1,noise=10)


plt.scatter(x,y)


plt.show()


# noise 越大的话，点就会越来越离散，例如 noise 由 10 变为 50.


x,y = datasets.make_regression(n_samples=100,n_features=1,n_targets=1,noise=50)


plt.scatter(x,y)


plt.show()

image-20180628094729828

image-20180628094801799

Sklearn常用属性和功能

以LinearRegression方法为例

  1. 导入：包、数据和模型

    1
    

    2
    

    3
    

    4
    

    5
    

    6
    

    7
    

    8
    

    from sklearn import datasets
    

    from sklearn.linear_model import LinearRegression
    

    

    loaded_data = datasets.load_boston()
    

    data_X = loaded_data.data
    

    data_y = loaded_data.target
    

    

    model = LinearRegression()

  2. 模型训练与预测

    1
    

    2
    

    3
    

    model.fit(data_X, data_y)
    

    

    print(model.predict(data_X[:4, :]))

  3. 模型参数

    模型：$f(x) = w_1x_1+w_2x_2+…+x_nw_n+w_0$

    model.coef_ 和 model.intercept_属于 Model 的属性

    model.coef_：模型权重，$(w_1,w_2,…,w_n)$

    model.intercept_：$w_0$

    1
    

    2
    

    3
    

    4
    

    5
    

    6
    

    7
    

    8
    

    9
    

    10
    

    11
    

    print(model.coef_)
    

    print(model.intercept_)
    

    

    

    """
    

    [ -1.07170557e-01   4.63952195e-02   2.08602395e-02   2.68856140e+00
    

      -1.77957587e+01   3.80475246e+00   7.51061703e-04  -1.47575880e+00
    

       3.05655038e-01  -1.23293463e-02  -9.53463555e-01   9.39251272e-03
    

      -5.25466633e-01]
    

    36.4911032804
    

    """

  4. 预测效果评分

    1
    

    2
    

    3
    

    4
    

    5
    

    print(model.score(data_X, data_y)) # R^2 coefficient of determination
    

    

    """
    

    0.740607742865
    

    """

    $R^2$计算方法：

    Screen Shot 2018-06-28 at 3.53.28 PM

正则化

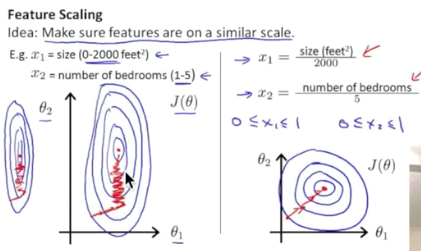
Screen Shot 2018-06-28 at 4.05.38 PM

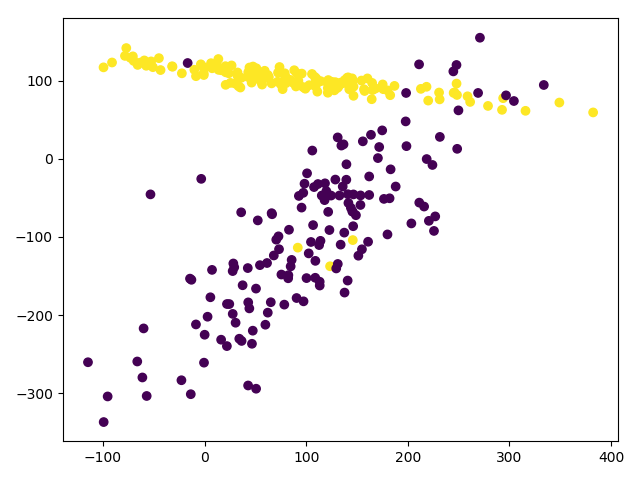
sklearn中模块preprocessing提供了scale功能。

1


2


3


4


5


6


7


8


9


10


11


12


13


from sklearn import preprocessing #标准化数据模块


import numpy as np




#建立Array


a = np.array([[10, 2.7, 3.6],


              [-100, 5, -2],


              [120, 20, 40]], dtype=np.float64)




#将normalized后的a打印出


print(preprocessing.scale(a)) #对每列进行单独的正则化


# [[ 0.         -0.85170713 -0.55138018]


#  [-1.22474487 -0.55187146 -0.852133  ]


#  [ 1.22474487  1.40357859  1.40351318]]


1


2


3


4


5


6


7


8


9


10


11


12


13


from sklearn import preprocessing


import numpy as np


from sklearn. model_selection import train_test_split


from sklearn.datasets.samples_generator import make_classification


from sklearn.svm import SVC


import matplotlib.pyplot as plt


##分类数据生成


x,y = make_classification(n_samples=300,n_features=2,


                          n_redundant=0,n_informative=2,


                          random_state=2,scale=100,


                          n_clusters_per_class=1)


plt.scatter(x[:,0],x[:,1],c=y)


plt.show()

image-20180628212803165

1


2


3


4


5


x_train,x_test,y_train,y_test = train_test_split(x,y,test_size=0.3)


clf = SVC()


clf.fit(x_train,y_train)


print(clf.score(x_test,y_test))


# 0.5111111111111111


1


2


3


4


5


6


7


x = preprocessing.scale(x)


plt.scatter(x[:,0],x[:,1],c=y)


plt.show() #可以看到坐标范围缩小了


x_train,x_test,y_train,y_test = train_test_split(x,y,test_size=0.3)


clf = SVC()


clf.fit(x_train,y_train)


print(clf.score(x_test,y_test))

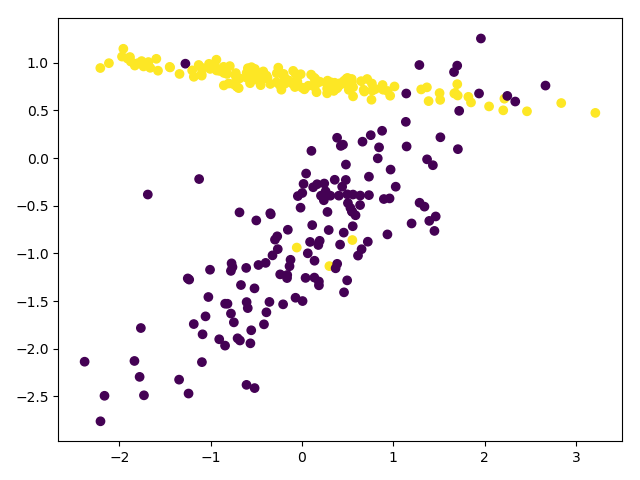
image-20180628213057808

交叉验证cross-validation

[Ref1] [Ref2]

Screen Shot 2018-07-12 at 10.12.09 AM

1


2


3


4


5


6


7


8


9


10


11


12


[M,N]=size(data);%数据集为一个M*N的矩阵，其中每一行代表一个样本


    indices=crossvalind('Kfold',data(1:M,N),10);%进行随机分包


    for k=1:10%交叉验证k=10，10个包轮流作为测试集


        test = (indices == k); %获得test集元素在数据集中对应的单元编号


        train = ~test;%train集元素的编号为非test元素的编号


        train_data=data(train,:);%从数据集中划分出train样本的数据


        train_target=target(:,train);%获得样本集的测试目标，在本例中是train样本的实际分类情况


        test_data=data(test,:);%test样本集


        test_target=target(:,test);%test的实际分类情况




        ...........


    end

有一个问题，k次训练会得到k个模型，也就是说每个模型的系数可能都不相同，那最终的模型是如何得到的呢？这个问题困扰了我很久。今天，通过阅读网上资料和matlab源码，解决这个问题，其实原理很简单。交叉验证只是一种模型验证方法，而不是一个模型优化方法，即用于评估一种模型在实际情况下的预测能力。比如，现在有若干个分类模型（决策树、SVM、KNN等），通过k-fold cross validation，可得到不同模型的误差值，进而选择最合适的模型，但是无法确定每个模型中的最优参数。

1


2


3


4


5


6


7


8


9


10


11


12


13


14


from sklearn.datasets import load_iris


from sklearn.model_selection import cross_val_score


from sklearn.neighbors import KNeighborsClassifier




iris = load_iris()


x = iris.data


y = iris.target




knn = KNeighborsClassifier()


scores = cross_val_score(knn,x,y,cv=5,scoring='accuracy')


print(scores)


# [0.96666667    1.    0.93333333   0.96666667   1.]


print(scores.mean())


# 0.9733333333333334


1


2


3


4


5


6


7


8


9


10


11


12


13


14


15


16


17


18


19


from sklearn.datasets import load_iris


from sklearn.model_selection import cross_val_score


from sklearn.neighbors import KNeighborsClassifier


import matplotlib.pyplot as plt




iris = load_iris()


x = iris.data


y = iris.target




neighbour_num = range(1,31)


k_score = []


for k in neighbour_num:


    knn = KNeighborsClassifier(n_neighbors=k)


    scores = cross_val_score(knn, x, y, cv=10, scoring='accuracy')


    k_score.append(scores.mean())


plt.plot(neighbour_num,k_score)


plt.xlabel('neighbour number')


plt.ylabel('cross-validated accuracy')


plt.show()

image-20180629095455584

1


2


3


4


5


6


7


8


9


10


11


12


13


14


15


16


17


18


19


from sklearn.datasets import load_iris


from sklearn.model_selection import cross_val_score


from sklearn.neighbors import KNeighborsClassifier


import matplotlib.pyplot as plt




iris = load_iris()


x = iris.data


y = iris.target




neighbour_num = range(1,31)


k_score = []


for k in neighbour_num:


    knn = KNeighborsClassifier(n_neighbors=k)


    loss = -cross_val_score(knn, x, y, cv=10, scoring='mean_squared_error')


    k_score.append(loss.mean())


plt.plot(neighbour_num,k_score)


plt.xlabel('neighbour number')


plt.ylabel('cross-validated MSE')


plt.show()

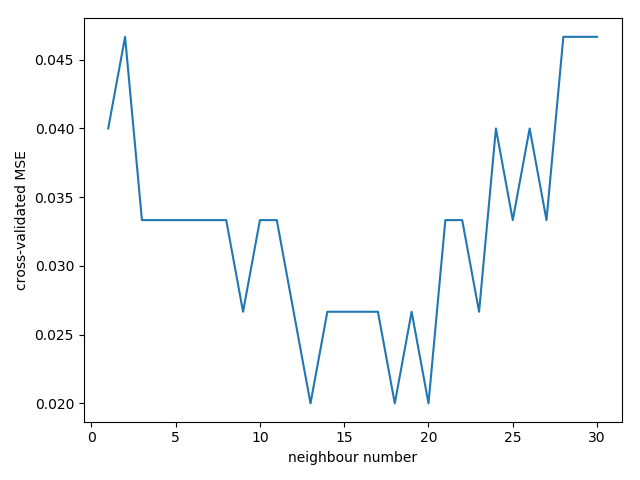
image-20180629095709851

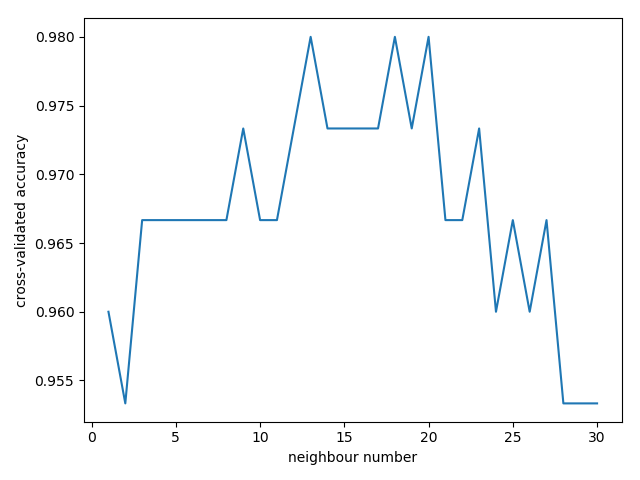
一般来说准确率(accuracy)会用于判断分类(Classification)模型的好坏。

平均方差(Mean squared error)会用于判断回归(Regression)模型的好坏。

Overfitting

  1. overfitting检查

    1
    

    2
    

    3
    

    4
    

    5
    

    6
    

    7
    

    8
    

    9
    

    10
    

    11
    

    12
    

    13
    

    14
    

    15
    

    16
    

    17
    

    18
    

    19
    

    20
    

    21
    

    22
    

    23
    

    24
    

    25
    

    26
    

    from sklearn.model_selection import learning_curve
    

    from sklearn.datasets import load_digits
    

    from sklearn.svm import SVC
    

    import matplotlib.pyplot as plt
    

    import numpy as np
    

    

    digits = load_digits()
    

    x = digits.data
    

    y = digits.target
    

    

    train_sizes,train_loss,test_loss = learning_curve(
    

        SVC(gamma=0.001),x,y,cv=10,
    

        scoring='mean_squared_error',
    

        train_sizes=[0.1,0.25,0.5,0.75,1])
    

    train_loss_mean = -np.mean(train_loss,axis=1)
    

    test_loss_mean = -np.mean(test_loss,axis=1)
    

    

    plt.plot(train_sizes, train_loss_mean, 'o-', color="r",
    

             label="Training")
    

    plt.plot(train_sizes, test_loss_mean, 'o-', color="g",
    

            label="Cross-validation")
    

    

    plt.xlabel("Training examples")
    

    plt.ylabel("Loss")
    

    plt.legend(loc="best")
    

    plt.show()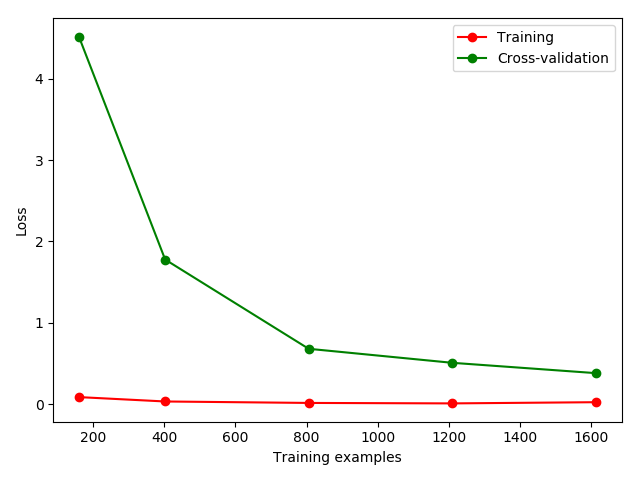

    image-20180701102341647

    • 加载digits数据集，其包含的是手写体的数字，从0到9。数据集总共有1797个样本，每个样本由64个特征组成， 分别为其手写体对应的8×8像素表示，每个特征取值0~16。
    • 采用K折交叉验证 cv=10, 选择平均方差检视模型效能 scoring='mean_squared_error', 样本由小到大分成5轮检视学习曲线(10%, 25%, 50%, 75%, 100%)
    • 从图中可以看出，随着训练样本的变大，训练误差和测试误差同时变小，说明模型的准确度因为样本增多而增高；

  2. 这次我们来验证SVC中的一个参数 gamma 在什么范围内能使 model 产生好的结果. 以及过拟合和 gamma 取值的关系.

    1
    

    2
    

    3
    

    4
    

    5
    

    6
    

    7
    

    8
    

    9
    

    10
    

    11
    

    12
    

    13
    

    14
    

    15
    

    16
    

    17
    

    18
    

    19
    

    20
    

    21
    

    22
    

    23
    

    24
    

    25
    

    26
    

    27
    

    28
    

    from sklearn.model_selection import validation_curve
    

    from sklearn.datasets import load_digits
    

    from sklearn.svm import SVC
    

    import matplotlib.pyplot as plt
    

    import numpy as np
    

    

    digits = load_digits()
    

    x = digits.data
    

    y = digits.target
    

    

    param_range = np.logspace(-6,-2.3,5)
    

    

    train_loss,test_loss = validation_curve(
    

        SVC(),x,y,param_name='gamma',
    

        param_range=param_range,cv=10,
    

        scoring='mean_squared_error')
    

    train_loss_mean = -np.mean(train_loss,axis=1)
    

    test_loss_mean = -np.mean(test_loss,axis=1)
    

    

    plt.plot(param_range, train_loss_mean, 'o-', color="r",
    

             label="Training")
    

    plt.plot(param_range, test_loss_mean, 'o-', color="g",
    

            label="Cross-validation")
    

    

    plt.xlabel("gamma")
    

    plt.ylabel("Loss")
    

    plt.legend(loc="best")
    

    plt.show()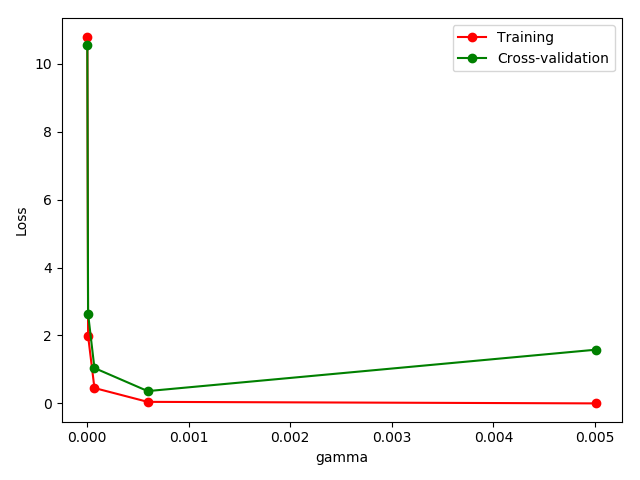

    image-20180701104019906

    从图中可以看到，当gamma从0到0.0005左右，training error和test error都在减小，说明模型效果随着gamma的最大而变好；但是当gamma继续增大，test error 却开始增加，说明gamma大于0.001时模型过拟合了。

模型保存

  1. pickle

    1
    

    2
    

    3
    

    4
    

    5
    

    6
    

    7
    

    8
    

    9
    

    10
    

    11
    

    12
    

    13
    

    14
    

    15
    

    16
    

    17
    

    18
    

    19
    

    20
    

    21
    

    from sklearn import svm
    

    from sklearn import datasets
    

    

    clf = svm.SVC()
    

    iris = datasets.load_iris()
    

    X, y = iris.data, iris.target
    

    clf.fit(X,y)
    

    

    import pickle #pickle模块
    

    

    #保存Model(注:save文件夹要预先建立，否则会报错)
    

    with open('save/clf.pickle', 'wb') as f:
    

        pickle.dump(clf, f)
    

    

    #读取Model
    

    with open('save/clf.pickle', 'rb') as f:
    

        clf2 = pickle.load(f)
    

        #测试读取后的Model
    

        print(clf2.predict(X[0:1]))
    

    

    # [0]

  2. joblib

    1
    

    2
    

    3
    

    4
    

    5
    

    6
    

    7
    

    8
    

    9
    

    10
    

    11
    

    12
    

    from sklearn.externals import joblib #jbolib模块
    

    

    #保存Model(注:save文件夹要预先建立，否则会报错)
    

    joblib.dump(clf, 'save/clf.pkl')
    

    

    #读取Model
    

    clf3 = joblib.load('save/clf.pkl')
    

    

    #测试读取后的Model
    

    print(clf3.predict(X[0:1]))
    

    

    # [0]