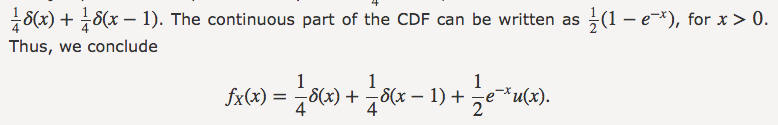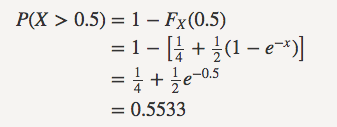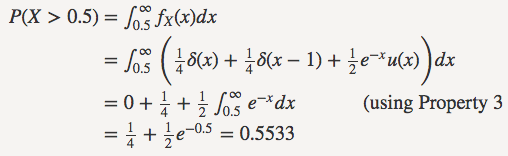Delta Function

Technically speaking, the Dirac delta function is not actually a function. It is what we may call a generalized function. Nevertheless, its definition is intuitive and it simplifies dealing with probability distributions.

Intuition ref2 begin to understand

Ref1 Google search

Unit Step function

在介绍delta函数之前，我们先了解一下阶跃函数(step function)，定义如下：

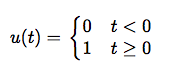
即当$t<0$时，函数值为0；否则，函数值是1。其图像如下：

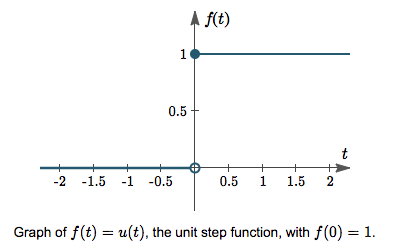
那么我们来求出阶跃函数的导数，显然当$t<0$和$t>0$时，导数是0，那么$t=0$呢？直觉上，在$t=0$处，函数的斜率是$\infin$，而实际上$t=0$处的导数就是$\infin$，证明可以参看阶跃函数的导数为什么是冲击函数?

$\delta$ Function

这样我们就得到了delta函数，$\delta$函数是在实数线上的一个函数，在原点上无限，在所有其他点上为零，

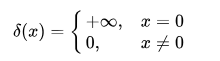
其图像是：

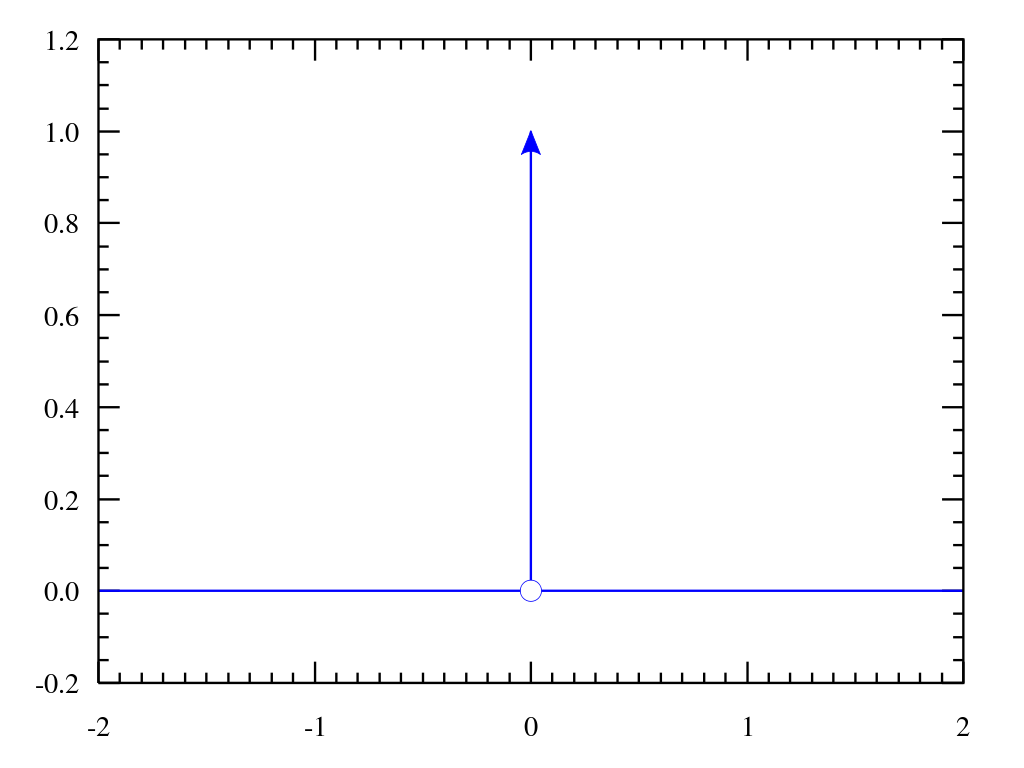
Properties

对于第三条性质，由于delta function是阶跃函数的导数，那么对其积分就对阶跃函数求函数值：

$$\int_{-\epsilon}^{\epsilon}\delta(x)dx=u(x)|_{-\epsilon}^{\epsilon}=u(\epsilon)-u(-\epsilon)=1-0=1$$

对于第四条性质，令$F(x)=g(x)\delta(x-x_0)$，根据$\delta$函数的定义，如果$x-x_0\ne 0$,即$x\ne x_0$，$\delta()=0$，即$F(x)=0$，那么可以改写上述为$F(x)=g(x_0)\delta (x-x_0)$，则

$$\int_{-\infin}^{\infin}g(x_0)\delta(x)dx=g(x_0)\int_{-\infin}^{\infin}\delta(x)dx=g(x_0)$$

Application

Delta Function in PDFs

无论是离散还是连续变量，它们都有连续累积函数(CDF)；而概率密度函数(PDF)，只存在于连续型变量；离散型变量有相应的概率质量函数(PMF)。使用$\delta$函数可以帮助我们对离散型变量和混合型变量定义一个PDF。

假设我们有一随机变量$X$，其取值为$R_X=\{x_1,x_2,x_3,…\}$，对应的PMF是$P_X(x_k)$。那么离散随机变量的CDF是一个阶梯函数，如下入所示

图中每一个跳跃点对应到横轴上都是一个$X$的取值，那么对于每一个$x_k$，其PMF为：

$$P_X(x_k)u(x-x_k)$$

即只有当$x=x_k$时，其概率是$P_X(x_k)$.

那么该随机变量$X$的CDF可以写作：

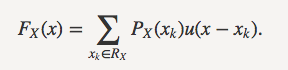
那么我们可以通过对CDF求导得到PDF，

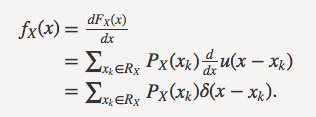
我们称之为generalized PDF

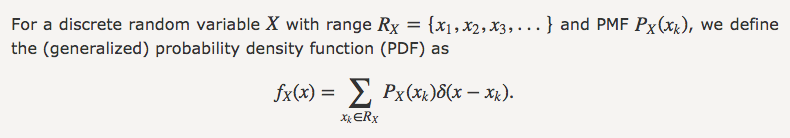
期望

对一个具有上述PDF的离散型变量X，其期望为：

$$\begin{equation} \begin{aligned} E(X)&=\int_{-\infin}^{\infin}xf_X(x)dx\\ &=\int_{-\infin}^{\infin}x\sum_{x_k\in R_X}P_X(x_k)\delta (x-x_k)dx\\ &=\sum_{x_k\in R_X}P_X(x_k)\int_{-\infin}^{\infin}x\delta (x-x_k)dx\\ &=\sum_{x_k\in R_X}P_X(x_k)x_k ------\text{4th property} \end{aligned} \end{equation}$$

可以看到，其期望值与离散型随机变量的定义一样。

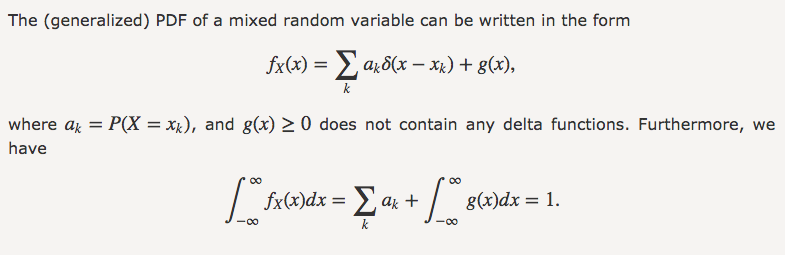
例子

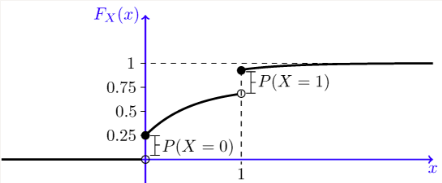
a. 画出CDF图像如下示：

可以看到有两个跳跃点$x=0$和$x=1$，同时在区间$[0,1)$和$[1,\infin]$，CDF又是连续的，所以随机变量$X$是一个混合型变量。

b. CDF有两个跳跃点，且每一个跳跃点的概率大小都是0.25，所以CDF有两个$\delta$函数：

c. 利用CDF，我们有：

利用PDF，我们有：

d.