Generative Adversarial Networks

Richard Feynman说“如果要真正理解一个东西，我们必须要能够把它创造出来。”

GAN 启发自博弈论中的二人零和博弈（two-player game），GAN 模型中的两位博弈方分别由生成式模型（generative model）和判别式模型（discriminative model）充当。生成模型 G 捕捉样本数据的分布，用服从某一分布（均匀分布，高斯分布等）的噪声 z 生成一个类似真实训练数据的样本，追求效果是越像真实样本越好；判别模型 D 是一个二分类器，估计一个样本来自于训练数据（而非生成数据）的概率，如果样本来自于真实的训练数据，D 输出大概率，否则，D 输出小概率。

intuition1 intuition2

code1 tensorflow-gan

video

Intuition

通常，我们会用下面这个例子来说明 GAN 的原理：将警察视为判别器，制造假币的犯罪分子视为生成器。一开始，犯罪分子会首先向警察展示一张假币。警察识别出该假币，并向犯罪分子反馈哪些地方是假的。接着，根据警察的反馈，犯罪分子改进工艺，制作一张更逼真的假币给警方检查。这时警方再反馈，犯罪分子再改进工艺。不断重复这一过程，直到警察识别不出真假，那么模型就训练成功了。

GAN强大之处在于可以自动的学习原始真实样本集的数据分布，GAN的生成模型最后可以通过噪声生成一个完整的真实数据（比如人脸），说明生成模型已经掌握了从随机噪声到人脸数据的分布规律了，有了这个规律，想生成人脸还不容易。然而这个规律我们开始知道吗？显然不知道，如果让你说从随机噪声到人脸应该服从什么分布，你不可能知道。这是一层层映射之后组合起来的非常复杂的分布映射规律。然而GAN的机制可以学习到，也就是说GAN学习到了真实样本集的数据分布。

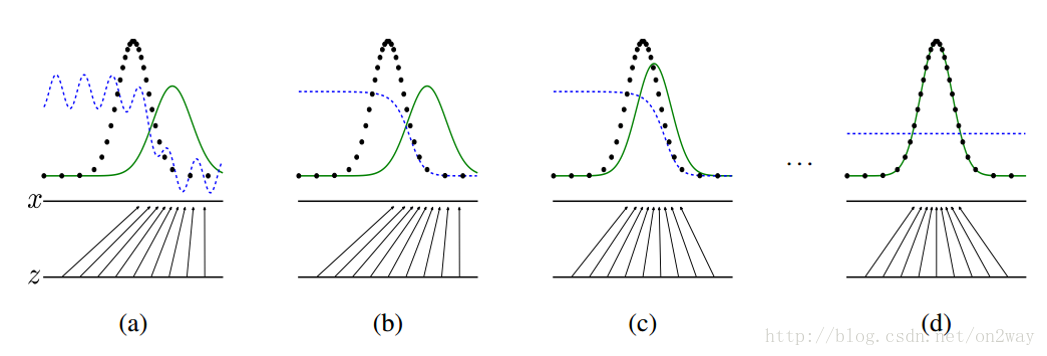
这张图表明的是GAN的生成网络如何一步步从均匀分布学习到正太分布的。原始数据x服从正太分布，这个过程你也没告诉生成网络说你得用正太分布来学习，但是生成网络学习到了。假设你改一下x的分布，不管什么分布，生成网络可能也能学到。

判别模型

假设现在生成网络模型已经有了（当然可能不是最好的生成网络），那么给一堆随机数组，就会得到一堆假的样本集（因为不是最终的生成模型，那么现在生成网络可能就处于劣势，导致生成的样本就不咋地，可能很容易就被判别网络判别出来了说这货是假冒的），但是先不管这个，假设我们现在有了这样的假样本集，真样本集一直都有，现在我们人为的定义真假样本集的标签，因为我们希望真样本集的输出尽可能为1，假样本集为0，很明显这里我们就已经默认真样本集所有的类标签都为1，而假样本集的所有类标签都为0. 有人会说，在真样本集里面的人脸中，可能张三人脸和李四人脸不一样呀，对于这个问题我们需要理解的是，我们现在的任务是什么，我们是想分样本真假，而不是分真样本中那个是张三label、那个是李四label。况且我们也知道，原始真样本的label我们是不知道的。回过头来，我们现在有了真样本集以及它们的label（都是1）、假样本集以及它们的label（都是0），这样单就判别网络来说，此时问题就变成了一个再简单不过的有监督的二分类问题了，直接送到神经网络模型中训练就完事了。假设训练完了，下面我们来看生成网络。

生成模型

对于生成网络，想想我们的目的，是生成尽可能逼真的样本。那么原始的生成网络生成的样本你怎么知道它真不真呢？就是送到判别网络中，所以在训练生成网络的时候，我们需要联合判别网络一起才能达到训练的目的。什么意思？就是如果我们单单只用生成网络，那么想想我们怎么去训练？误差来源在哪里？细想一下没有，但是如果我们把刚才的判别网络串接在生成网络的后面，这样我们就知道真假了，也就有了误差了。所以对于生成网络的训练其实是对生成-判别网络串接的训练。好了那么现在来分析一下样本，原始的噪声数组Z我们有，也就是生成了假样本我们有，此时很关键的一点来了，我们要把这些假样本的标签都设置为1，也就是认为这些假样本在生成网络训练的时候是真样本。那么为什么要这样呢？我们想想，是不是这样才能起到迷惑判别器的目的，也才能使得生成的假样本逐渐逼近为正样本。好了，重新顺一下思路，现在对于生成网络的训练，我们有了样本集（只有假样本集，没有真样本集），有了对应的label（全为1），是不是就可以训练了？有人会问，这样只有一类样本，训练啥呀？谁说一类样本就不能训练了？只要有误差就行。还有人说，你这样一训练，判别网络的网络参数不是也跟着变吗？没错，这很关键，所以在训练这个串接的网络的时候，一个很重要的操作就是不要判别网络的参数发生变化，也就是不让它参数发生更新，只是把误差一直传，传到生成网络那块后更新生成网络的参数。这样就完成了生成网络的训练了。

在完成生成网络训练好，那么我们是不是可以根据目前新的生成网络再对先前的那些噪声Z生成新的假样本了，没错，并且训练后的假样本应该是更真了才对。然后又有了新的真假样本集（其实是新的假样本集），这样又可以重复上述过程了。我们把这个过程称作为单独交替训练。我们可以实现定义一个迭代次数，交替迭代到一定次数后停止即可。这个时候我们再去看一看噪声Z生成的假样本会发现，原来它已经很真了。

损失函数

对于判别器$D$，其优化函数：

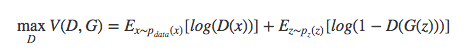
对于生成器$G$，其优化函数：

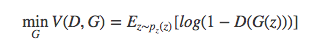
GAN的特殊理解

GAN的目标是学习一个从指定分布数据到目标分布数据的映射，一旦学习好了这个映射，我们则需要比较这两个分布的相近程度，注意不是比较样本之间的差距。通常我们会用考KL距离来描述这两个分布的差异，但是GAN并没有指定任何距离，而是学习出一个距离度量。

假设我们的GAN的网络参数是$\theta$, 目标分布是$z_i$，拟合出来的分布是$y_i$，那么GAN有一个独立的距离度量网络$L$，输入$z_i$和$y_i$，自动计算分布的差异，即：

$$L(\{z_i\}_{i=1}^{M},\{y_i\}_{i=1}^{N},\theta)$$

考虑到$\{z_i\}_{i=1}^{M}$是已知的，我们可以将之视作非变量，当成模型的一部分，则上式可以简写为：

$$L(\{y_i\}_{i=1}^{N},\theta)$$

但是，我们比较的是分布间的距离，即分布本身与各个$y_i$出现的顺序是没有关系的，因此，尽管$L$是各个$y_i$和函数，但它必须全对称，

$$L = \frac{1}{M!}\sum_{对y_1, ..., y_M所有的排列求和}D(y_1,y_2,...,\Theta)$$

也就是说，我们先找⼀个有序的函数$D$，然后对所有可能的序求平均，那么就得到⽆序的函数了。当然，这样的计算量是$O(M!)$，显然也不靠谱，那么我们就选择最简单的⼀种：

$$L=\frac{1}{M} \sum_{i=1}^{M} D\left(y_{i}, \Theta\right)$$

这便是⽆序的最简单实现，可以简单的理解为：分布之间的距离，等于单个样本的距离的平均。

因为$D(Y,\theta)$的均值, 也就是$L$, 是度量两个分布的差异程度, 这就意味着，要能够将两个分布区分开来，即$L$越⼤越好；但是我们最终的⽬的，是希望通过均匀分布⽽⽣成我们指定的分布，所以$G(X,\theta)$则希望两个分布越来越接近，即$L$越⼩越好。

训练$D(Y,\Theta)$的时候，我们随机初始化$G(X,\theta)$，固定它，然后生成一批$Y$。我们再从目标样本中采样一批$Z$，则

$$\begin{array}{l}{\Theta=\arg \min L=\underset{\Theta}{\arg \min } \frac{1}{N} \sum_{i=1}^{N} D\left(z_{i}, \Theta\right)} \\ {\Theta=\arg \max L=\underset{\Theta}{\arg \max } \frac{1}{M} \sum_{i=1}^{M} D\left(y_{i}, \Theta\right)}\end{array}$$

然⽽有两个⽬标并不容易平衡，所以⼲脆都取同样的样本数$B$（⼀个batch），然后⼀起训练就好：

$$\begin{array}{l}{\Theta=\arg \min _{\boldsymbol{\theta}} L_{1}} \\ {\quad=\underset{\Theta}{\arg \min } \frac{1}{B} \sum_{i=1}^{B}\left[D\left(z_{i}, \Theta\right)-D\left(y_{i}, \Theta\right)\right]}\end{array}$$

而$G(X,\theta)$希望⽣成的样本越接近真实样本越好，因此这时候把$D$的参数$\Theta$固定，只训练 $\theta$让$L$越来越⼩：

$$\begin{aligned} \theta &=\underset{\theta}{\arg \min } L_{2} \\ &=\underset{\theta}{\arg \min } \frac{1}{B} \sum_{i=1}^{B}\left[D\left(G\left(x_{i}, \theta\right), \Theta\right)\right] \end{aligned}$$

实际上，传统的GAN公式如下

局限

existing problems

在手写体数字生成过程中，我们无法得知什么样的噪声z可以用来生成数字1，什么样的噪声z可以用来生成数字3，我们对这些一无所知，这从一点程度上限制了我们对GAN的使用。

GAN实现

GAN训练伪代码

这里红框圈出的部分是我们要额外注意的。第一步我们训练D，D是希望V(G, D)越大越好，所以是加上梯度(ascending)。第二步训练G时，V(G, D)越小越好，所以是减去梯度(descending)。整个训练过程交替进行。

keras实现手写体

文字版 Tensorflow实现手写体

'''
DCGAN on MNIST using Keras
Author: Rowel Atienza
Project: https://github.com/roatienza/Deep-Learning-Experiments
Dependencies: tensorflow 1.0 and keras 2.0
Usage: python3 dcgan_mnist.py
'''

import numpy as np
import time
from tensorflow.examples.tutorials.mnist import input_data

from keras.models import Sequential
from keras.layers import Dense, Activation, Flatten, Reshape
from keras.layers import Conv2D, Conv2DTranspose, UpSampling2D
from keras.layers import LeakyReLU, Dropout
from keras.layers import BatchNormalization
from keras.optimizers import Adam, RMSprop

import matplotlib.pyplot as plt

class ElapsedTimer(object):
    def __init__(self):
        self.start_time = time.time()
    def elapsed(self,sec):
        if sec < 60:
            return str(sec) + " sec"
        elif sec < (60 * 60):
            return str(sec / 60) + " min"
        else:
            return str(sec / (60 * 60)) + " hr"
    def elapsed_time(self):
        print("Elapsed: %s " % self.elapsed(time.time() - self.start_time) )

class DCGAN(object):
    def __init__(self, img_rows=28, img_cols=28, channel=1):

        self.img_rows = img_rows
        self.img_cols = img_cols
        self.channel = channel
        self.D = None   # discriminator
        self.G = None   # generator
        self.AM = None  # adversarial model
        self.DM = None  # discriminator model

    # (W−F+2P)/S+1
    def discriminator(self):
        if self.D:
            return self.D
        self.D = Sequential()
        depth = 64
        dropout = 0.4
        # In: 28 x 28 x 1, depth = 1
        # Out: 14 x 14 x 1, depth=64
        input_shape = (self.img_rows, self.img_cols, self.channel)
        self.D.add(Conv2D(depth*1, 5, strides=2, input_shape=input_shape,\
            padding='same'))
        self.D.add(LeakyReLU(alpha=0.2))
        self.D.add(Dropout(dropout))

        self.D.add(Conv2D(depth*2, 5, strides=2, padding='same'))
        self.D.add(LeakyReLU(alpha=0.2))
        self.D.add(Dropout(dropout))

        self.D.add(Conv2D(depth*4, 5, strides=2, padding='same'))
        self.D.add(LeakyReLU(alpha=0.2))
        self.D.add(Dropout(dropout))

        self.D.add(Conv2D(depth*8, 5, strides=1, padding='same'))
        self.D.add(LeakyReLU(alpha=0.2))
        self.D.add(Dropout(dropout))

        # Out: 1-dim probability
        self.D.add(Flatten())
        self.D.add(Dense(1))
        self.D.add(Activation('sigmoid'))
        self.D.summary()
        return self.D

    def generator(self):
        if self.G:
            return self.G
        self.G = Sequential()
        dropout = 0.4
        depth = 64+64+64+64
        dim = 7
        # In: 100
        # Out: dim x dim x depth
        self.G.add(Dense(dim*dim*depth, input_dim=100))
        self.G.add(BatchNormalization(momentum=0.9))
        self.G.add(Activation('relu'))
        self.G.add(Reshape((dim, dim, depth)))
        self.G.add(Dropout(dropout))

        # In: dim x dim x depth
        # Out: 2*dim x 2*dim x depth/2
        self.G.add(UpSampling2D())
        self.G.add(Conv2DTranspose(int(depth/2), 5, padding='same'))
        self.G.add(BatchNormalization(momentum=0.9))
        self.G.add(Activation('relu'))

        self.G.add(UpSampling2D())
        self.G.add(Conv2DTranspose(int(depth/4), 5, padding='same'))
        self.G.add(BatchNormalization(momentum=0.9))
        self.G.add(Activation('relu'))

        self.G.add(Conv2DTranspose(int(depth/8), 5, padding='same'))
        self.G.add(BatchNormalization(momentum=0.9))
        self.G.add(Activation('relu'))

        # Out: 28 x 28 x 1 grayscale image [0.0,1.0] per pix
        self.G.add(Conv2DTranspose(1, 5, padding='same'))
        self.G.add(Activation('sigmoid'))
        self.G.summary()
        return self.G

    def discriminator_model(self):
        if self.DM:
            return self.DM
        optimizer = RMSprop(lr=0.0002, decay=6e-8)
        self.DM = Sequential()
        self.DM.add(self.discriminator())
        self.DM.compile(loss='binary_crossentropy', optimizer=optimizer,\
            metrics=['accuracy'])
        return self.DM

    def adversarial_model(self):
        if self.AM:
            return self.AM
        optimizer = RMSprop(lr=0.0001, decay=3e-8)
        self.AM = Sequential()
        self.AM.add(self.generator())
        self.AM.add(self.discriminator())
        self.AM.compile(loss='binary_crossentropy', optimizer=optimizer,\
            metrics=['accuracy'])
        return self.AM

class MNIST_DCGAN(object):
    def __init__(self):
        self.img_rows = 28
        self.img_cols = 28
        self.channel = 1

        self.x_train = input_data.read_data_sets("mnist",\
        	one_hot=True).train.images
        self.x_train = self.x_train.reshape(-1, self.img_rows,\
        	self.img_cols, 1).astype(np.float32)

        self.DCGAN = DCGAN()
        self.discriminator =  self.DCGAN.discriminator_model()
        self.adversarial = self.DCGAN.adversarial_model()
        self.generator = self.DCGAN.generator()

    def train(self, train_steps=2000, batch_size=256, save_interval=0):
        noise_input = None
        if save_interval>0:
            noise_input = np.random.uniform(-1.0, 1.0, size=[16, 100])
        for i in range(train_steps):
            images_train = self.x_train[np.random.randint(0,
                self.x_train.shape[0], size=batch_size), :, :, :]
            noise = np.random.uniform(-1.0, 1.0, size=[batch_size, 100])
            images_fake = self.generator.predict(noise)
            x = np.concatenate((images_train, images_fake))
            y = np.ones([2*batch_size, 1])
            y[batch_size:, :] = 0
            d_loss = self.discriminator.train_on_batch(x, y)

            y = np.ones([batch_size, 1])
            noise = np.random.uniform(-1.0, 1.0, size=[batch_size, 100])
            a_loss = self.adversarial.train_on_batch(noise, y)
            log_mesg = "%d: [D loss: %f, acc: %f]" % (i, d_loss[0], d_loss[1])
            log_mesg = "%s  [A loss: %f, acc: %f]" % (log_mesg, a_loss[0], a_loss[1])
            print(log_mesg)
            if save_interval>0:
                if (i+1)%save_interval==0:
                    self.plot_images(save2file=True, samples=noise_input.shape[0],\
                        noise=noise_input, step=(i+1))

    def plot_images(self, save2file=False, fake=True, samples=16, noise=None, step=0):
        filename = 'mnist.png'
        if fake:
            if noise is None:
                noise = np.random.uniform(-1.0, 1.0, size=[samples, 100])
            else:
                filename = "mnist_%d.png" % step
            images = self.generator.predict(noise)
        else:
            i = np.random.randint(0, self.x_train.shape[0], samples)
            images = self.x_train[i, :, :, :]

        plt.figure(figsize=(10,10))
        for i in range(images.shape[0]):
            plt.subplot(4, 4, i+1)
            image = images[i, :, :, :]
            image = np.reshape(image, [self.img_rows, self.img_cols])
            plt.imshow(image, cmap='gray')
            plt.axis('off')
        plt.tight_layout()
        if save2file:
            plt.savefig(filename)
            plt.close('all')
        else:
            plt.show()

if __name__ == '__main__':
    mnist_dcgan = MNIST_DCGAN()
    timer = ElapsedTimer()
    mnist_dcgan.train(train_steps=10000, batch_size=256, save_interval=500)
    timer.elapsed_time()
    mnist_dcgan.plot_images(fake=True)
    mnist_dcgan.plot_images(fake=False, save2file=True)