AutoEncoder（自编码器）本质上是数据特定的数据压缩。虽然自编码器中的重构损失函数确保了编码过程原始数据不会丢失过多，但是没有对约束特征$z$做出约束。

作为一种无监督的学习方法，VAE（Variational Auto-Encoder，变分自编码器）是一个产生式模型，其在ae的基础上约束潜变量$z$服从于某个已知的先验分布$p(z|x)$，比如希望$z$的每个特征相互独立并且符合高斯分布等。

判别式模型 VS 生成式模型

ref1 ref2

给定数据样本$D=\{x_1,x_2,…,x_n\}$，及其对应的标签$\{y_1,y_2,…,y_n\}$.

判别式模型：直接对$p(y|x)$进行建模

生成式模型：对$x$和$y$的联合分布$p(x,y)$进行建模，然后通过贝叶斯公式来求得$p(y|x)$，最后选择使$p(y|x)$最大的$y_i$。

判别式模型大多有下面的规律：已知观察变量X，和隐含变量z，判别式模型对p(z|X)进行建模，它根据输入的观察变量x得到隐含变量z出现的可能性。生成式模型则是将两者的顺序反过来，它要对p(X|z)进行建模，输入是隐含变量，输出是观察变量的概率。

可以想象，不同的模型结构自然有不同的用途。判别模型在判别工作上更适合，生成模型在分布估计等问题上更有优势。如果想用生成式模型去解决判别问题，就需要利用贝叶斯公式把这个问题转换成适合自己处理的样子：

$p(z | X)=\frac{p(X | z) p(z)}{p(X)}$

对于一些简单的问题，上面的公式还是比较容易解出的，但对于一些复杂的问题，找出从隐含变量到观察变量之间的关系是一件很困难的事情，生成式模型的建模过程会非常困难，所以对于判别类问题，判别式模型一般更适合。

但对于“随机生成满足某些隐含变量特点的数据”这样的问题来说，判别式模型就会显得力不从心。如果用判别式模型生成数据，就要通过类似于下面这种方式的方法进行。

第一步，利用简单随机一个X。

第二步，用判别式模型计算p(z|X)概率，如果概率满足，则找到了这个观察数据，如果不满足，返回第一步。

这样用判别式模型生成数据的效率可能会十分低下。而生成式模型解决这个问题就十分简单，首先确定好z的取值，然后根据p(X|z)的分布进行随机采样就行了

Intuition behind VAE

该部分参考了ZhiHu-VAE.

考虑MNIST数据集，数据集里有10种数字，每种数字下有几千个不同的样本，我们能不能照猫画虎，模仿已有的数字生成一个同样可辨识，但却与现有的样本都不同的的数字呢？

要解决这个问题，需要对数字的分布进行建模。我们需要知道一个数字“一般而言长什么样”。如果我们得到了数据集X的分布P(X)，那么数据集中的每个图片，也不过就是从P(X)采样得到的一个样本而已。可以说掌握了P(X)，我们就算把这个数据集的底裤都扒下来了，到时候搓扁捏圆，任君所愿。

然而从有限的样本中估计出数据原来的分布情况，却不是一件容易的事，别说更复杂的数据集了，就是MNIST你也做不好。为了能估计P(X)，我们做一个隐变量假设，假设数据集X实际上是由一组我们观察不到的隐变量Z经过某个复杂的映射$P(z|x)$产生的，给定一个z，我就能通过某种方法生成一个样本$\hat x$。如果能得到z的分布和$P(z|x)$，那P(X)我们也算知道了。

这个假设是有道理的，z尽管是隐变量，但不妨碍我们对它的物理含义做出猜测。比方说z里面有控制笔画粗细的变量，有控制笔划角度的变量，有控制数字大小的变量等等。这些变量一旦确定，写出来的数字大致长什么样就确定了。

但是，P(X)分布的形式未知这点很好理解，但凭什么P(Z)能服从标准n维高斯分布呢？比方z里面有个控制比划粗细的变量，它怎么可能是高斯分布呢？答案隐藏在$P(z|x)$中：对于任意d维随机变量，不管他们实际上服从什么分布，我总可以用d个服从标准高斯分布的随机变量通过一个足够复杂的函数去逼近它。我们可以这样理解，z其实是“隐变量的隐变量”，函数$P(z|x)$实际上首先将z映射到某一组隐变量z’，这个z’可能就是上面说的笔划粗细啊，角度什么的有物理含义的东西，然后接着再把z’映射到X得到样本。

Network Structure

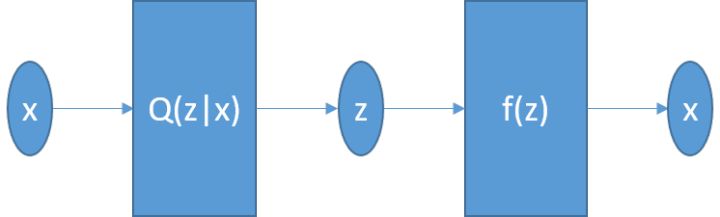
v2-0533fd3dc73184f807038b4f08e8681a_hd

变分编码器和自动编码器的区别就在于，传统自动编码器的隐变量z的分布是不知道的，因此我们无法采样得到新的z，也就无法通过解码器得到新的x。下面我们来变分，我们现在不要从x中直接得到z，而是得到z的均值和方差，然后再迫使它逼近正态分布的均值和方差，则网络变成下面的样子：

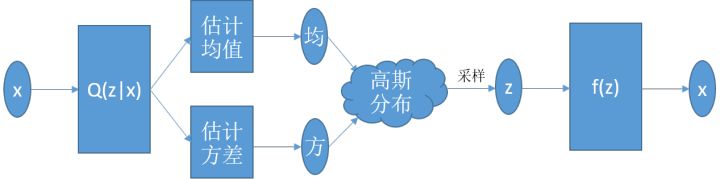
v2-89c7d409bcb7a8218c80b3134b015818_hd

看上去不错，从Q(z|x)估计出来的值跟标准正态分布不一样没关系，训练过程中慢慢逼近就行了。假定z服从高斯分布的好处之一在这里就能体现出来，只要估计均值和方差，我们就完全了解这个高斯分布了，也就能从其中采样了。

然而上面这个网络最大的问题是，它是断开的。前半截是从数据集估计z的分布，后半截是从一个z的样本重构输入。最关键的采样这一步，恰好不是一个我们传统意义上的操作。这个网络没法求导，因为梯度传到f(z)以后没办法往前走了。

为了使得整个网络得以训练，使用一种叫reparemerization的trick，使得网络对均值和方差可导，把网络连起来。这个trick的idea见下图：

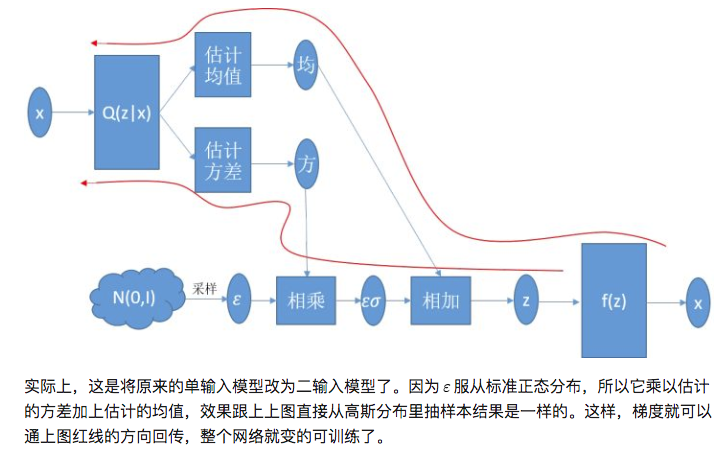
Screen Shot 2018-07-24 at 1.05.03 PM

Math in VAE

REF

Intro

假设我们有一批数据样本$\left\{X_{1}, \ldots, X_{n}\}\right.$, 其整体用$X$来描述，我们想用$\left\{X_{1}, \ldots, X_{n}\}\right.$得到$X$的分布$p(X)$，如果可以实现的话，那我们就可以根据$p(X)$来采样，就可能得到所有可能的$X$了，包括$\left\{X_{1}, \ldots, X_{n}\}\right.$以外的样本，这就是一个生成模型了。但是这个很难去实现，于是我们将分布改一下：

$p(X)=\sum_{Z} p(X | Z) p(Z)$

此时$p(X|Z)$描述了一个由$Z$生成$X$的模型，如果我们假设$Z$服从标准正态分布，即$p(Z)=\mathcal{N}(0, I)$ 。

如果这个实现，我们就可以先从标准正态分布中采样一个$Z$，然后根据$Z$来算一个$X$，也是一个很棒的生成模型。接下来就是结合自编码器来实现重构，保证有效信息没有丢失，再加上一系列的推导，最后把模型实现。框架的示意图如下：

68990612

但是，在整个VAE模型中，我们并没有去使用$p(Z)$（隐变量空间的分布）是正态分布的假设，我们用的是假设$p(Z|X)$（后验分布）是正态分布！！

具体来说，给定一个真实样本$Xk$，我们假设存在一个专属于$Xk$的分布$p(Z|X_k)$（学名叫后验分布），并进一步假设这个分布是（独立的、多元的）正态分布。为什么要强调“专属”呢？因为我们后面要训练一个生成器$X=g(Z)$，希望能够把从分布$p(Z|X_k)$采样出来的一个$Z_k$还原为$X_k$。如果假设$p(Z)$是正态分布，然后从$p(Z)$中采样一个$Z$，那么我们怎么知道这个$Z$对应于哪个真实的$X$呢？现在$p(Z|X_k)$专属于$X_k$，我们有理由说从这个分布采样出来的ZZ应该要还原到$X_k$中去。

这时候每一个$X_k$都配上了一个专属的正态分布，才方便后面的生成器做还原。但这样有多少个$X$就有多少个正态分布了。我们知道正态分布有两组参数：均值$\mu$和方差$\sigma^2$（多元的话，它们都是向量），那我怎么找出专属于$X_k$的正态分布$p(Z|X_k)$的均值和方差呢？用神经网络来拟合出来吧！

于是我们构建两个神经网络$\mu_k=f_1(X_k),log\sigma^{2}_k=f_2(X_k)$来算它们了。我们选择拟合$log\sigma^2_k$而不是直接拟合$\sigma^2_k$，是因为$\sigma^2_k$总是非负的，需要加激活函数处理，而拟合$log\sigma^2_k$不需要加激活函数，因为它可正可负。到这里，我能知道专属于$X_k$的均值和方差了，也就知道它的正态分布长什么样了，然后从这个专属分布中采样一个$Z_k$出来，然后经过一个生成器得到$\hat X_k=g(Z_k)$，现在我们可以放心地最小化$\mathcal{D}\left(\hat{X}_{k}, X_{k}\right)^{2}$，因为$Z_k$是从专属$X_k$的分布中采样出来的，这个生成器应该要把开始的$X_k$还原回来。于是可以画出VAE的示意图

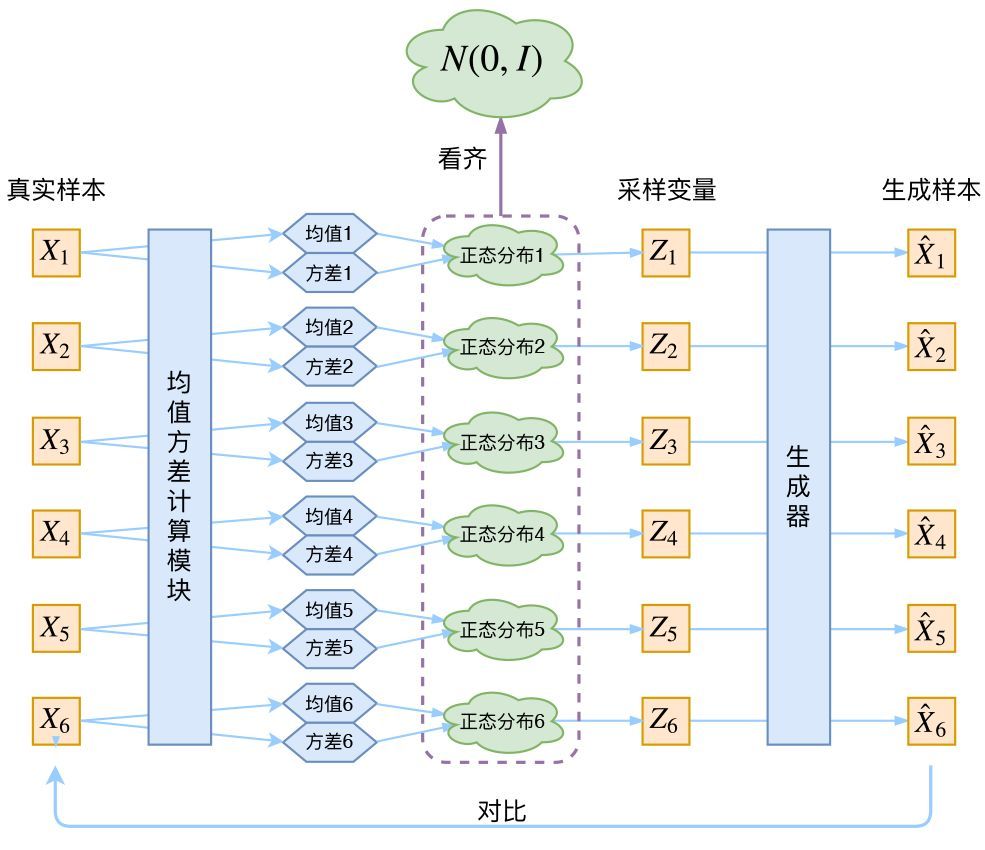
8da0009b298c462b9dba190f21f594f5

让我们来思考一下，根据上图的训练过程，最终会得到什么结果。

首先，我们希望重构$X$，也就是最小化$\mathcal{D}\left(\hat{X}_{k}, X_{k}\right)^{2}$，但是这个重构过程受到噪声的影响，因为$Z_k$是通过重新采样过的，不是直接由encoder算出来的。显然噪声会增加重构的难度，不过好在这个噪声强度（也就是方差）通过一个神经网络算出来的，所以最终模型为了重构得更好，肯定会想尽办法让方差为0。而方差为0的话，也就没有随机性了，所以不管怎么采样其实都只是得到确定的结果（也就是均值），只拟合一个当然比拟合多个要容易，而均值是通过另外一个神经网络算出来的。

说白了，模型会慢慢退化成普通的AutoEncoder，噪声不再起作用。

这样不就白费力气了吗？说好的生成模型呢？

别急别急，其实VAE还让所有的$p(Z|X)$都向标准正态分布看齐，这样就防止了噪声为零，同时保证了模型具有生成能力。怎么理解“保证了生成能力”呢？如果所有的$p(Z|X)$都很接近标准正态分布$N(0,I)$，那么根据定义

$p(Z)=\sum_{X} p(Z | X) p(X)=\sum_{X} \mathcal{N}(0, I) p(X)=\mathcal{N}(0, I) \sum_{X} p(X)=\mathcal{N}(0, I)$

这样我们就能达到我们的先验假设：$p(Z)$是标准正态分布。然后我们就可以放心地从$N(0,I)$中采样来生成图像了。

那如何让$p(Z|X)$接近标准正态分布$N(0,I)$呢？其实最直接的方法应该是在重构误差的基础上中加入额外的loss：

$\mathcal{L}_{\mu}=\left\|f_{1}\left(X_{k}\right)\right\|^{2} \quad \mathbb{and} \quad \mathcal{L}_{\sigma^{2}}=\left\|f_{2}\left(X_{k}\right)\right\|^{2}$

因为它们分别代表了均值$\mu_k$和方差的对数$\log \sigma_{k}^{2}$，达到$N(0,I)$就是希望二者尽量接近0。不过，这又会面临着这两个损失的比例要怎么选取的问题，选取得不好，生成的图像会比较模糊。所以，原论文直接算了一般（各分量独立的）正态分布与标准正态分布的KL散度$K L\left(N\left(\mu, \sigma^{2}\right) | N(0, I)\right)$作为这个额外的loss，计算结果为：

$\mathcal{L}_{\mu, \sigma^{2}}=\frac{1}{2} \sum_{i=1}^{d}\left(\mu_{(i)}^{2}+\sigma_{(i)}^{2}-\log \sigma_{(i)}^{2}-1\right)$

这里$d$是隐变量$Z$的维度，而$\mu_{(i)}$和$\log \sigma_{(i)}^{2}$分别代表一般正态分布的均值向量和方差向量的第$i$个分量。直接用这个式子做补充loss，就不用考虑均值损失和方差损失的相对比例问题了。显然，这个loss也可以分两部分理解：

$\begin{array}{l}{\mathcal{L}_{\mu, \sigma^{2}}=\mathcal{L}_{\mu}+\mathcal{L}_{\sigma^{2}}} \\ {\mathcal{L}_{\mu}=\frac{1}{2} \sum_{i=1}^{d} \mu_{(i)}^{2}=\frac{1}{2}\left\|f_{1}(X)\right\|^{2}} \\ {\mathcal{L}_{\sigma^{2}}=\frac{1}{2} \sum_{i=1}^{d}\left(\sigma_{(i)}^{2}-\log \sigma_{(i)}^{2}-1\right)}\end{array}$

推导

由于我们考虑的是各分量独立的多元正态分布，因此只需要推导一元正态分布的情形即可，根据定义我们可以写出
$\begin{aligned} & K L\left(N\left(\mu, \sigma^{2}\right) \| N(0,1)\right) \\=& \int \frac{1}{\sqrt{2 \pi \sigma^{2}}} e^{-(x-\mu)^{2} / 2 \sigma^{2}}\left(\log \frac{e^{-(x-\mu)^{2} / 2 \sigma^{2}} / \sqrt{2 \pi \sigma^{2}}}{e^{-x^{2} / 2} / \sqrt{2 \pi}}\right) d x \\=& \int \frac{1}{\sqrt{2 \pi \sigma^{2}}} e^{-(x-\mu)^{2} / 2 \sigma^{2}} \log \left\{\frac{1}{\sqrt{\sigma^{2}}} \exp \left\{\frac{1}{2}\left[x^{2}-(x-\mu)^{2} / \sigma^{2}\right]\right\}\right\} d x \\=& \frac{1}{2} \int \frac{1}{\sqrt{2 \pi \sigma^{2}}} e^{-(x-\mu)^{2} / 2 \sigma^{2}}\left[-\log \sigma^{2}+x^{2}-(x-\mu)^{2} / \sigma^{2}\right] d x \end{aligned}$
整个结果分为三项积分，第一项实际上就是$-\log \sigma^{2}$乘以概率密度的积分（也就是1），所以结果是$-\log \sigma^{2}$; 第二项实际是正态分布的二阶矩，熟悉正态分布的朋友应该都清楚正态分布的二阶矩为$\mu^{2}+\sigma^{2}$；而根据定义，第三项实际上就是“-方差除以方差=-1”。所以总结果就是
$K L\left(N\left(\mu, \sigma^{2}\right) \| N(0,1)\right)=\frac{1}{2}\left(-\log \sigma^{2}+\mu^{2}+\sigma^{2}-1\right)$

Reparemerization(重参)

其实很简单，就是我们要从$p(Z|X_k)$中采样一个$Z_k$出来，尽管我们知道了$p(Z|X_k)$是正态分布，但是均值方差都是靠模型算出来的，我们要靠这个过程反过来优化均值方差的模型，但是“采样”这个操作是不可导的，而采样的结果是可导的。我们利用

$\begin{aligned} & \frac{1}{\sqrt{2 \pi \sigma^{2}}} \exp \left(-\frac{(z-\mu)^{2}}{2 \sigma^{2}}\right) d z \\=& \frac{1}{\sqrt{2 \pi}} \exp \left[-\frac{1}{2}\left(\frac{z-\mu}{\sigma}\right)^{2}\right] d\left(\frac{z-\mu}{\sigma}\right) \end{aligned}$

这说明$(z-\mu) / \sigma=\varepsilon$是服从均值为0、方差为1的标准正态分布的，要同时把$dz$考虑进去，是因为乘上$dz$才算是概率，去掉$dz$是概率密度而不是概率。这时候我们得到：

从$\mathcal{N}\left(\mu, \sigma^{2}\right)$ 中采样一个$Z$，相当于从$N(0,I)$中采样一个$\boldsymbol{\varepsilon}$ ，然后让$Z=\mu+\varepsilon \times c$。

于是，我们将从$\mathcal{N}\left(\mu, \sigma^{2}\right)$采样变成了从$N(0,I)$中采样，然后通过参数变换得到从$\mathcal{N}\left(\mu, \sigma^{2}\right)$ 中采样的结果。这样一来，“采样”这个操作就不用参与梯度下降了，改为采样的结果参与，使得整个模型可训练了。

Screen Shot 2018-07-23 at 11.15.34 PM

intuition

采样操作是不可导，采样之后的加减操作是可导，所以利用了重参技巧？

可以参考这篇文章. 如下图，左边是直接sample隐变量，显然，无法对这个“动作”进行任何数学计算；但是，使用了重参，即右边部分将隐变量的sample变成了一个数学计算，$z = \epsilon*\sigma+\mu$，显然可导。

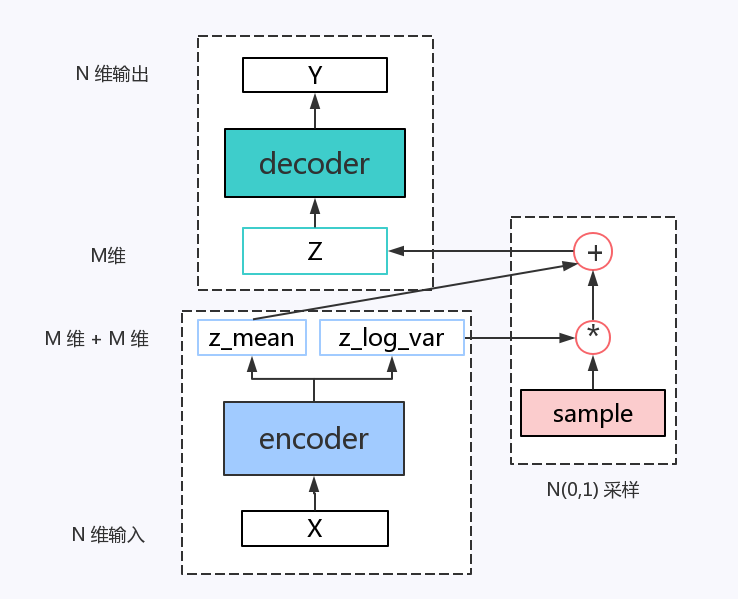
Screen Shot 2018-07-23 at 11.16.40 PM

由于训练过程只用到 X（同时作为输入和目标输出），而与 X的标签无关，因此，这是无监督学习。

Screen Shot 2018-07-22 at 1.12.06 AM

The generated image is linear combination of existing images.

VAE数据流动和损失计算

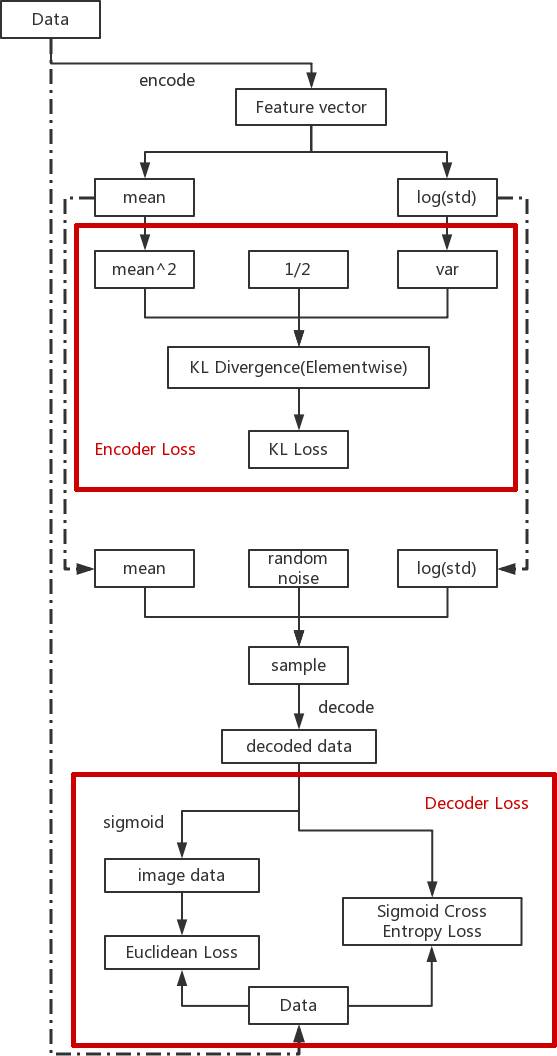
VAE的Keras实现

detailed explanation

点击显/隐内容

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
 
from keras.layers import Input, Dense, Lambda
from keras.models import Model
from keras import backend as K
from keras import objectives
from keras.datasets import mnist
from keras.utils.visualize_util import plot
import sys

Encoder

输入是$n$维，输出$x\times m$维

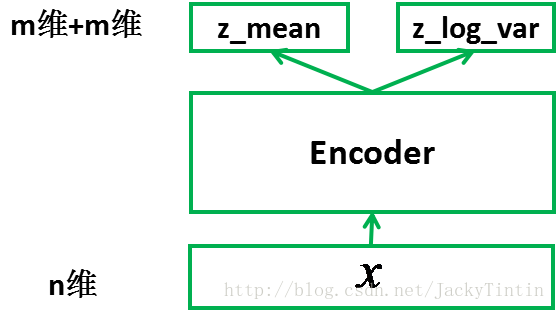
20161214175120686

点击显/隐内容

batch_size = 100
original_dim = 784  # 28*28
latent_dim = 2 # encoder output size
intermediate_dim = 256 # neural number of hidden layer
nb_epoch = 50
epsilon_std = 1.0 

x = Input(batch_shape=(batch_size, original_dim))
h = Dense(intermediate_dim, activation='relu')(x)
z_mean = Dense(latent_dim)(h)
z_log_var = Dense(latent_dim)(h)

Sampling

将encoder的大小为$(2\times m)$的输出视作$m$个高斯多元分布的均值$z_{mean}$和方差的对数$z _ log _ var$

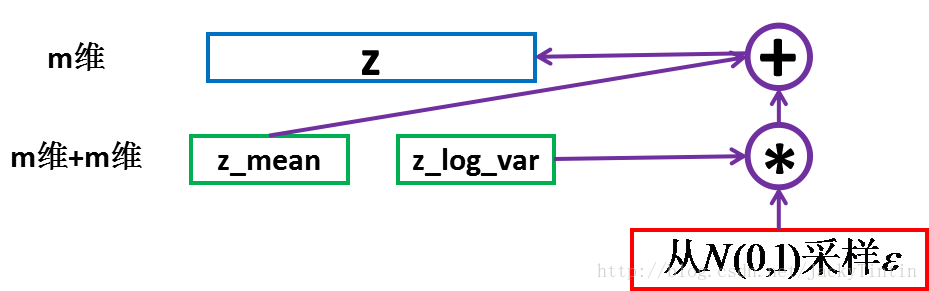
20161214175146348

点击显/隐内容

def sampling(args):
  z_mean, z_log_var = args
  epsilon = K.random_normal(shape=(batch_size, latent_dim), mean=0.,stddev=epsilon_std)
  return z_mean + K.exp(z_log_var / 2) * epsilon

z = Lambda(sampling, output_shape=(latent_dim,))([z_mean, z_log_var])

Decoder

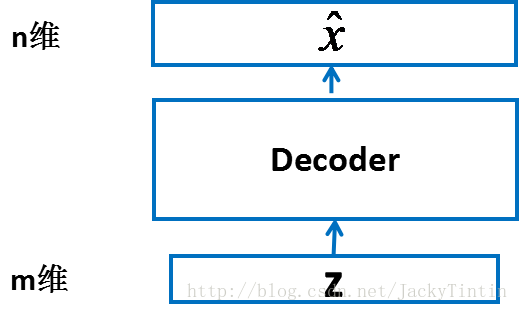
20161214175029514

点击显/隐内容

decoder_h = Dense(intermediate_dim, activation='relu')
decoder_mean = Dense(original_dim, activation='sigmoid')
h_decoded = decoder_h(z)
x_decoded_mean = decoder_mean(h_decoded)

Loss Function

点击显/隐内容

def vae_loss(x, x_decoded_mean):
  # my tips:logloss
  xent_loss = original_dim * objectives.binary_crossentropy(x, x_decoded_mean)
  # my tips:see paper's appendix B
  kl_loss = - 0.5 * K.sum(1 + z_log_var - K.square(z_mean) - K.exp(z_log_var), axis=-1)
  return xent_loss + kl_loss

Training

点击显/隐内容

vae = Model(x, x_decoded_mean)
vae.compile(optimizer='rmsprop', loss=vae_loss)

# train the VAE on MNIST digits
(x_train, y_train), (x_test, y_test) = mnist.load_data(path='mnist.pkl.gz')

x_train = x_train.astype('float32') / 255. # input normalization
x_test = x_test.astype('float32') / 255.
x_train = x_train.reshape((len(x_train), np.prod(x_train.shape[1:])))
x_test = x_test.reshape((len(x_test), np.prod(x_test.shape[1:])))

vae.fit(x_train, # regarded as "x", which is "training data"
        x_train, # regarded as "y", which is "target/label data"
        shuffle=True,
        nb_epoch=nb_epoch,
        verbose=2,# Verbosity mode. 0 = silent, 1 = progress bar, 2 = one line per epoch.
        batch_size=batch_size,
        validation_data=(x_test, x_test))

Latent space display

点击显/隐内容

# build a model to project inputs on the latent space
encoder = Model(x, z_mean)
# display a 2D plot of the digit classes in the latent space
x_test_encoded = encoder.predict(x_test, batch_size=batch_size)
plt.figure(figsize=(6, 6))
plt.scatter(x_test_encoded[:, 0], x_test_encoded[:, 1], c=y_test)
plt.colorbar()
plt.show()

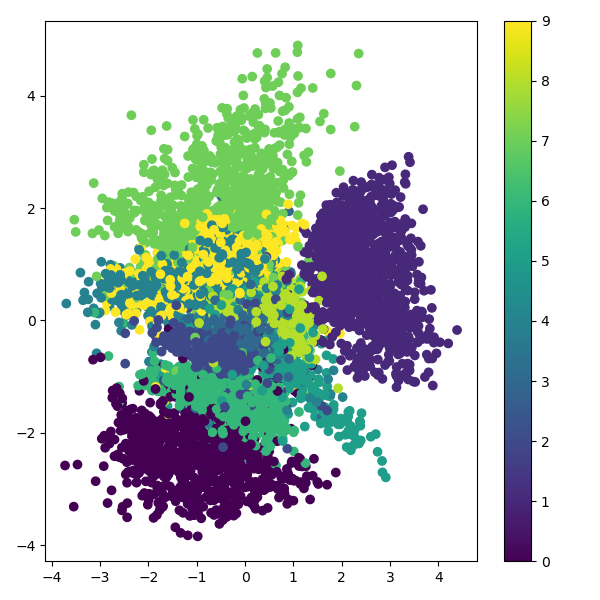
Generated pics display

点击显/隐内容

# build a digit generator that can sample from the learned distribution
decoder_input = Input(shape=(latent_dim,))
_h_decoded = decoder_h(decoder_input)
_x_decoded_mean = decoder_mean(_h_decoded)
generator = Model(decoder_input, _x_decoded_mean)

# display a 2D manifold of the digits
n = 15  # figure with 15x15 digit pics
digit_size = 28 # size of the pic is 28*28
figure = np.zeros((digit_size * n, digit_size * n))

xy = np.linspace(0.05, 0.95, n) # generate n number in range(0.05,0.95)
grid_x = norm.ppf(xy) # ppf is a inverse function of CDF, e.g. xy=0.1,then ppf return x such that p(X<x)=0.1
grid_y = norm.ppf(xy)

#plotting
for i, yi in enumerate(grid_x):
    for j, xi in enumerate(grid_y):
        z_sample = np.array([[xi, yi]])#1*2
        x_decoded = generator.predict(z_sample)
        digit = x_decoded[0].reshape(digit_size, digit_size)#the generated image
        figure[i * digit_size: (i + 1) * digit_size,
               j * digit_size: (j + 1) * digit_size] = digit

plt.figure(figsize=(10, 10))
plt.imshow(figure, cmap='Greys_r')
plt.show()

Reference

AE to VAE AE vs VAE intuition3 gotcha

ref1 ref2 ref3 ref4 [intuition about learn latent gaussian distribution] ref7 VAE vs GAN

video1 公式