Tree | Blog of Qing

树的定义

#Definition for a binary tree node.
class TreeNode:
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None

树的遍历

Pre-order ：root， (left)，(right)

class Solution:
    def helper(self,root):
        if not root:return 
        self.res.append(root.val)
        self.helper(root.left)
        self.helper(root.right)
    def preorderTraversal(self, root):
        self.res = []
        if not root:return self.res
        self.helper(root)
        return self.res

In-order： (left)，root，(right)

class Solution:
    def helper(self,root):
        if not root:return 
        self.helper(root.left)
        self.res.append(root.val)
        self.helper(root.right)
    def inorderTraversal(self, root):
        self.res = []
        if not root:return self.res
        self.helper(root)
        return self.res

Post-order： (left)，(right)，root

class Solution:
    def helper(self,root):
        if not root:return 
        self.helper(root.left)
        self.helper(root.right)
        self.res.append(root.val)
    def postorderTraversal(self, root):
        self.res = []
        if not root:return self.res
        self.helper(root)
        return self.res

队列

try:
    import Queue as queue
except ImportError:
    import queue #python2.+
#定义一个队列
import queue #python3.+
qu = queue.Queue()
#入队列
qu.put(xx)
#出队列
qu.get()
#队列大小
qu.qsize()
#队列空
qu.empty()

简单

Merge Two Binary Trees

题目 )

点击显/隐内容

Given two binary trees and imagine that when you put one of them to cover the other, some nodes of the two trees are overlapped while the others are not.

You need to merge them into a new binary tree. The merge rule is that if two nodes overlap, then sum node values up as the new value of the merged node. Otherwise, the NOT null node will be used as the node of new tree.

Example 1:

Input: 
	Tree 1                     Tree 2                  
          1                         2                             
         / \                       / \                            
        3   2                     1   3                        
       /                           \   \                      
      5                             4   7                  
Output: 
Merged tree:
	     3
	    / \
	   4   5
	  / \   \ 
	 5   4   7

思路

题目大意：将两棵树合并，合并规则：对应位置的节点值相加成为新的节点；如果两个节点中有一个空节点，则另一个非空节点成为新的节点。

显然是递归求解啊，使用递归时候，考虑一个节点的情况，剩下的节点就递归调用。考虑两棵树的根节点，如果有一棵树是空，那么就不要合并了，直接返回另一棵树；如果都不空，则将两个根节点相加成为新节点值，该新节点的左子树就使用两棵树的左子树作为参数递归调用，同理右子树。

代码

点击显/隐内容

class Solution:
    def mergeTrees(self, t1, t2):
        if not t1:return t2
        if not t2:return t1
        t1.val += t2.val
        t1.left = self.mergeTrees(t1.left,t2.left)
        t1.right = self.mergeTrees(t1.right,t2.right)
        return t1

Find Mode in Binary Search Tree

题目

点击显/隐内容

Given a binary search tree (BST) with duplicates, find all the mode(s)) (the most frequently occurred element) in the given BST.

Assume a BST is defined as follows:

The left subtree of a node contains only nodes with keys less than or equal to the node’s key.
The right subtree of a node contains only nodes with keys greater than or equal to the node’s key.
Both the left and right subtrees must also be binary search trees.

For example:
Given BST [1,null,2,2],

return [2].

思路

题目大意：给定一棵平衡搜索树，该树的父节点值可以等于孩子节点值，要求找出该树出现次数最多的节点值。

最简单的做法就是设置一个字典，记录每个节点出现次数，然后遍历该树。

代码

点击显/隐内容

import collections
class Solution:
    def find(self,root,dic):
        if root:
            dic[root.val]+=1
            dic = self.find(root.left,dic)
            dic = self.find(root.right,dic)
        return dic
    def findMode(self, root):
        re = []
        if not root:return re
        dic = collections.defaultdict(int)
        dic = self.find(root,dic)
        fre = collections.Counter(dic).most_common(1)[0][1]
        for k,v in dic.items():
            if v==fre:
                re.append(k)
        return re

Sum of Left Leaves

题目

点击显/隐内容

Find the sum of all left leaves in a given binary tree.

Example:

    3
   / \
  9  20
    /  \
   15   7

There are two left leaves in the binary tree, with values 9 and 15 respectively. Return 24.

思路

题目大意：求左叶子节点的和；

关于左叶子，前提它是叶子，同时又位于一个节点的左边。

递归求解，重点是如何判断一个节点是左叶子？只要该节点是左节点且其左右子树均是空，那么就可以返回改点的值，同时递归该点的右兄弟节点。

代码

点击显/隐内容

class Solution:
    def sumOfLeftLeaves(self, root):
        if not root:return 0
        if root.left and not root.left.left and not root.left.right:
            return root.left.val + self.sumOfLeftLeaves(root.right)
        return self.sumOfLeftLeaves(root.left) + self.sumOfLeftLeaves(root.right)

Maximum Depth of Binary Tree

题目

点击显/隐内容

Given a binary tree, find its maximum depth.

The maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.

Note: A leaf is a node with no children.

Example:

Given binary tree [3,9,20,null,null,15,7],

return its depth = 3.

思路

题目大意：求树的最大高度。

递归求解，对于一个结点，如果是空，则返回高度0；否则需要递归求解器左右子树的高度，那么该节点的高度是1+max( length_left_tree , length_right_tree ).

代码

点击显/隐内容

class Solution:
    def maxDepth(self, root):
        if not root:return 0
        l = self.maxDepth(root.left)
        r = self.maxDepth(root.right)
        return max(l,r)+1

Convert Sorted Array to Binary Search Tree

题目

点击显/隐内容

Given an array where elements are sorted in ascending order, convert it to a height balanced BST.

For this problem, a height-balanced binary tree is defined as a binary tree in which the depth of the two subtrees of every node never differ by more than 1.

Example:

Given the sorted array: [-10,-3,0,5,9],

One possible answer is: [0,-3,9,-10,null,5], which represents the following height balanced BST:

      0
     / \
   -3   9
   /   /
 -10  5

思路

题目大意：将一个有序上升的数组还原成一棵二分搜索树。

为了使左右子树的高度差不超过1，则每次选择中点作为根，根左边的数组作为左子树，右边的数组作为右子树，递归建树。

代码

点击显/隐内容

class Solution:
    def sortedArrayToBST(self, nums):
        if not nums:return None
        mid = len(nums)//2
        root = TreeNode(nums[mid])
        l = self.sortedArrayToBST(nums[0:mid])
        r = self.sortedArrayToBST(nums[mid+1:])
        root.left = l
        root.right = r
        return root

Binary Tree Paths

题目

点击显/隐内容

Given a binary tree, return all root-to-leaf paths.

Note: A leaf is a node with no children.

Example:

Input:

   1
 /   \
2     3
 \
  5

Output: ["1->2->5", "1->3"]

Explanation: All root-to-leaf paths are: 1->2->5, 1->3

思路

题目大意：写出树的所有路径。

递归遍历。

代码

点击显/隐内容

Invert Binary Tree

题目

点击显/隐内容

Invert a binary tree.

Example:

Input:

     4
   /   \
  2     7
 / \   / \
1   3 6   9

Output:

     4
   /   \
  7     2
 / \   / \
9   6 3   1

思路

题目大意：交换二叉树中所有节点的左右子树。

递归。对于一个节点，判断空，如是返回空；否则，递归invert其左子树和右子树，然后交换。

代码

点击显/隐内容

class Solution:
    def invertTree(self, root):
        """
        :type root: TreeNode
        :rtype: TreeNode
        """
        if not root:return None
        l = self.invertTree(root.left)
        r = self.invertTree(root.right)
        root.left = r
        root.right = l
        return root

Same Tree

题目

点击显/隐内容

Given two binary trees, write a function to check if they are the same or not.

Two binary trees are considered the same if they are structurally identical and the nodes have the same value.

Example 1:

Input:     1         1
          / \       / \
         2   3     2   3

        [1,2,3],   [1,2,3]

Output: true

Example 2:

Input:     1         1
          /           \
         2             2

        [1,2],     [1,null,2]

Output: false

Example 3:

Input:     1         1
          / \       / \
         2   1     1   2

        [1,2,1],   [1,1,2]

Output: false

思路

题目大意是要判断是否两棵树相同，相同的要求是具有相同的结构且节点值一致。比较简单，使用递归的方法，两棵树的相对节点，判断其值是否相同，如果相同，则递归判断其左子树和右子树。

代码

点击显/隐内容

class Solution:
    def isSameTree(self, p, q):
        """
        :type p: TreeNode
        :type q: TreeNode
        :rtype: bool
        """
        if not p or not q:
            return p==q
        elif p.val == q.val:
            return self.isSameTree(p.left,q.left) and self.isSameTree(p.right,q.right)
        return False

Binary Tree Level Order Traversal II

题目

点击显/隐内容

Given a binary tree, return the bottom-up level order traversal of its nodes’ values. (ie, from left to right, level by level from leaf to root).

For example:
Given binary tree [3,9,20,null,null,15,7],

return its bottom-up level order traversal as:

[
  [15,7],
  [9,20],
  [3]
]

思路

这道题就是对树进行广度遍历，借助队列。需要注意的是：在判断队列是否为空，需要检查其队列大小。

代码

点击显/隐内容

import queue
class Solution:
    def levelOrderBottom(self, root):
        if not root:
            return []
        nodes = []
        qu = queue.Queue()
        qu.put(root)
        while qu.qsize()>0: 
            l = qu.qsize()
            node = []
            for i in range(l):
                front = qu.get()
                node.append(front.val)
                if front.left:
                    qu.put(front.left)
                if front.right:
                    qu.put(front.right)
            nodes.insert(0,node)
        return nodes

Path Sum

题目

点击显/隐内容

Given a binary tree and a sum, determine if the tree has a root-to-leaf path such that adding up all the values along the path equals the given sum.

Note: A leaf is a node with no children.

Example:

Given the below binary tree and sum = 22,

      5
     / \
    4   8
   /   / \
  11  13  4
 /  \      \
7    2      1

return true, as there exist a root-to-leaf path 5->4->11->2 which sum is 22.

思路

题目大意：求是否存在一条根到叶子的路径，使路径和等于给定的目标值。

递归求解，每次判断是否该节点的值等于目标值，且该点是否叶子，如果是，则找到了；否则，递归判断左子树和右子树，但是，此时目标值应该更新为（目标值-节点值）。

代码

点击显/隐内容

class Solution:
    def hasPathSum(self, root, sum):
        if not root : return False
        if root.val == sum and not root.left and not root.right: return True
        l,r = False, False
        if root.left:
            l = self.hasPathSum(root.left,sum-root.val)
        if root.right:
            r = self.hasPathSum(root.right,sum-root.val)
        return l or r

中等

Binary Tree Tilt

题目

点击显/隐内容

Given a binary tree, return the tilt of the whole tree.

The tilt of a tree node is defined as the absolute difference between the sum of all left subtree node values and the sum of all right subtree node values. Null node has tilt 0.

The tilt of the whole tree is defined as the sum of all nodes’ tilt.

Example:

Input: 
         1
       /   \
      2     3
Output: 1
Explanation: 
Tilt of node 2 : 0
Tilt of node 3 : 0
Tilt of node 1 : |2-3| = 1
Tilt of binary tree : 0 + 0 + 1 = 1

思路

题目大意：求解树所有节点倾斜度的和。一个节点倾斜度定义为其左子树节点和与右子树节点和的绝对值差。

利用后续遍历，那么就会从叶结点开始处理，这样我们就能很方便的计算结点的累加和，同时也可以很容易的根据子树和来计算tilt。

代码

点击显/隐内容

class Solution:
    def helper(self,root):
        if not root:return 0
        l = self.helper(root.left)
        r = self.helper(root.right)
        self.tilt += abs(l-r)
        return l+r+root.val
        
    def findTilt(self, root):
        self.tilt = 0
        self.helper(root)
        return self.tilt

Subtree of Another Tree

题目

点击显/隐内容

Given two non-empty binary trees s and t, check whether tree t has exactly the same structure and node values with a subtree of s. A subtree of s is a tree consists of a node in s and all of this node’s descendants. The tree s could also be considered as a subtree of itself.

Example 1:
Given tree s:

Given tree t:

1
2
3

  4 
 / \
1   2

Return

true

, because t has the same structure and node values with a subtree of s.

Example 2:
Given tree s:

Given tree t:

1
2
3

  4
 / \
1   2

Return false

思路

题目大意：判断一棵树是否为另一棵树的子树。子树要求从某一个节点开始之叶子，完全相同。

递归。以根节点为例，如果两棵树的根节点都是空，则算子树；如果有一个节点是空，则不能是。这样保证了都不空情况下，判断节点值是否相等，相等则递归左右子树。

代码

点击显/隐内容

class Solution:
    def helper(self,s,t):
        if not t and not s:return True
        if not s or not t:return False
        if s.val != t.val:return False
        return self.helper(s.left,t.left) and self.helper(s.right,t.right)
        pass
    def isSubtree(self, s, t):
        if not s:return False
        if self.helper(s,t):return True
        lflag = self.isSubtree(s.left,t)
        rflag = self.isSubtree(s.right,t)
        return lflag or rflag

Construct String from Binary Tree

题目

点击显/隐内容

You need to construct a string consists of parenthesis and integers from a binary tree with the preorder traversing way.

The null node needs to be represented by empty parenthesis pair “()”. And you need to omit all the empty parenthesis pairs that don’t affect the one-to-one mapping relationship between the string and the original binary tree.

Example 1:

Input: Binary tree: [1,2,3,4]
       1
     /   \
    2     3
   /    
  4     

Output: "1(2(4))(3)"

Explanation: Originallay it needs to be "1(2(4)())(3()())", 
but you need to omit all the unnecessary empty parenthesis pairs. 
And it will be "1(2(4))(3)".

Example 2:

Input: Binary tree: [1,2,3,null,4]
       1
     /   \
    2     3
     \  
      4 

Output: "1(2()(4))(3)"

Explanation: Almost the same as the first example, 
except we can't omit the first parenthesis pair to break the one-to-one mapping relationship between the input and the output.

思路

题目大意：按照树的结构将节点值写出一个序列，根节点在前面，使用括弧将左子树包起来，使用另一个括弧将右子树包起来，不允许空的括弧。但是，根据上面的两个例子，在某些情况下又必须保留空括弧，如果将例子2中的括弧删去，则例子1和例子2有相同的序列，但是他们是不同的树。那么，什么情况下需要保留空括弧呢？即左子树空但是右子树不空。递归解决，考虑根节点，先递归求解出左子树序列，右子树序列；然后整合序列：右子树不空（不论左子树是否空），root(left)(right)；否则左子树不空（右子树空），root(left)；左右子树都空时，root

代码

点击显/隐内容

class Solution:
    def tree2str(self, t):
        res = ''
        if not t:return res
        lres = self.tree2str(t.left)
        rres = self.tree2str(t.right)
        if rres:
            return str(t.val)+'(%s)'%lres+'(%s)'%rres
        elif lres:
            return str(t.val)+'(%s)'%lres
        else:
            return str(t.val)

Two Sum IV - Input is a BST

题目

点击显/隐内容

Given a Binary Search Tree and a target number, return true if there exist two elements in the BST such that their sum is equal to the given target.

Example 1:

Input: 
    5
   / \
  3   6
 / \   \
2   4   7

Target = 9

Output: True

Example 2:

Input: 
    5
   / \
  3   6
 / \   \
2   4   7

Target = 28

Output: False

思路

题目大意：在一棵二分搜索树上查找是否存在两个数，使这两个数的和恰为给定的以目标值。

二分搜索树，中序遍历之后的节点值是一个递增序列，这样我们就可以使用2-sum方法求解。使用两个指针，分别指向序列的第一个元素和最后一个元素，比较两个指针指向值的和与目标值的大小关系。相等，结束；目标值比较大，两个元素的和比较大，则右指针左移，欲尝试更小的和；如果两个元素的和比较小，则左指针右移。

代码

点击显/隐内容

class Solution:
    def inorder(self,root,node_list):
        if root.left:
            self.inorder(root.left,node_list)
        node_list.append(root.val)
        if root.right:
            self.inorder(root.right,node_list)
    def findTarget(self, root, k):
        if not root:return False
        node_list = []
        self.inorder(root,node_list)
        start = 0
        end = len(node_list)-1
        while start<end:
            if node_list[start]+node_list[end]==k:
                return True
            elif node_list[start]+node_list[end]<k:
                start += 1
            else:
                end -= 1
        return False

Longest Univalue Path

题目

点击显/隐内容

Given a binary tree, find the length of the longest path where each node in the path has the same value. This path may or may not pass through the root.

Note: The length of path between two nodes is represented by the number of edges between them.

Example 1:

Input:

Output:

Example 2:

Input:

Output:

思路

题目大意：找出树上最长路径，使该路径上每个节点值都相同。并不要求该路径一定要经过根，路径上边的数量表示路径长度。

这道题的思路类似Path Sum III，因为允许不经过root。首先来分析节点值相同的路径的集中情况，题目给出的两个例子包含了所有的两种情况：例子1是路径由父母节点和其某个子树构成；例子2路径存在某个子树中，不经过父亲节点。

情况一：如果根节点的值与子节点值相同，那么递归求解左右子树下的路径，然后选择长度更长的路径+1。

情况二：如果根节点的值与子节点值相同，那么递归求解左右子树下的路径，最长路径由左子树-根-右子树组成。

代码

点击显/隐内容

class Solution(object):
    def find(self,rootval,root):
        if not root or rootval!=root.val :return 0
        l = self.find(root.val,root.left)
        r = self.find(root.val,root.right)
        return 1+max(l,r)
        
    def longestUnivaluePath(self, root):
        if not root:return 0
        l = self.longestUnivaluePath(root.left)
        r = self.longestUnivaluePath(root.right)
        return max( max(l,r), self.find(root.val,root.left)+self.find(root.val,root.right) )

Second Minimum Node In a Binary Tree

题目

点击显/隐内容

Given a non-empty special binary tree consisting of nodes with the non-negative value, where each node in this tree has exactly twoor zero sub-node. If the node has two sub-nodes, then this node’s value is the smaller value among its two sub-nodes.

Given such a binary tree, you need to output the second minimum value in the set made of all the nodes’ value in the whole tree.

If no such second minimum value exists, output -1 instead.

Example 1:

Input: 
    2
   / \
  2   5
     / \
    5   7

Output: 5
Explanation: The smallest value is 2, the second smallest value is 5.

Example 2:

Input: 
    2
   / \
  2   2

Output: -1
Explanation: The smallest value is 2, but there isn't any second smallest value.

思路

题目大意：给定一棵树，这棵树上的节点要么没有子树，要么一定有左右子树而且左右子树的节点值一定不小于该节点值。现在求该树上的第二小的值。

根据该树的描述，根节点一定是最小的，那么就遍历树找比根节点大，但又小于剩下的节点值。那么如何找出满足条件的值呢？我们初始化secondNum=max_value，每次遍历一个节点，只要满足root.val<current_node.val<secondNum，我们就更新：secondNum=current_node.val。使用DFS和BFS两种方法遍历，发现第一种方法更快。dfs:36ms 而bfs:44ms

代码

点击显/隐内容

import sys
class Solution:
    def dfs(self,root,first,second):
        if first<root.val<second:
            second = root.val
        if root.left:
            second = self.dfs(root.left,first,second)
            second = self.dfs(root.right,first,second)
        return second
    def findSecondMinimumValue(self, root):
        """
        :type root: TreeNode
        :rtype: int
        """
        if not root:return -1
        second = sys.maxsize
        second = self.dfs(root,root.val,second)
        if second == sys.maxsize:
            return -1
        else:
            return second

import queue
import sys
class Solution:
    def findSecondMinimumValue(self, root):
        """
        :type root: TreeNode
        :rtype: int
        """
        secondNum = sys.maxsize
        if not root:return -1
        qu = queue.Queue()
        qu.put(root)
        while qu.qsize()>0:
            node = qu.get()
            if node.val>root.val and node.val<secondNum:
                secondNum = node.val
            if node.left:
                qu.put(node.left)
                qu.put(node.right)
        if secondNum==sys.maxsize:
            return -1
        else:
            return secondNum

Binary Tree Paths

题目

点击显/隐内容

Given a binary tree, return all root-to-leaf paths.

Note: A leaf is a node with no children.

Example:

Input:

   1
 /   \
2     3
 \
  5

Output: ["1->2->5", "1->3"]

Explanation: All root-to-leaf paths are: 1->2->5, 1->3

思路

题目大意：找到一棵树的全部路径。

递归求解，如果碰到一个节点是叶子，即没有左右子树，则找到了一条路径，返回。否则，将该节点值加入路径，然后递归求解其左右子树。

代码

点击显/隐内容

class Solution:
    def find(self,result,root, string):
        if not root.left and not root.right:
            result.append(string)
            return result
        if root.left:
            result = self.find(result,root.left,string+'->'+str(root.left.val))
        if root.right:
            result = self.find(result,root.right,string+'->'+str(root.right.val))
        return result
    def binaryTreePaths(self, root):
        """
        :type root: TreeNode
        :rtype: List[str]
        """
        result = []
        if not root:return result
        return self.find(result,root,str(root.val))

Lowest Common Ancestor of a Binary Search Tree

题目

点击显/隐内容

Given a binary search tree (BST), find the lowest common ancestor (LCA) of two given nodes in the BST.

According to the definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).”

Given binary search tree: root = [6,2,8,0,4,7,9,null,null,3,5]

     _______6______
    /              \
 ___2__          ___8__
/      \        /      \
0      _4       7       9
      /  \
      3   5

Example 1:

1
2
3

Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
Output: 6
Explanation: The LCA of nodes 2 and 8 is 6.

Example 2:

Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
Output: 2
Explanation: The LCA of nodes 2 and 4 is 2, since a node can be a descendant of itself 
             according to the LCA definition.

Note:

All of the nodes’ values will be unique.
p and q are different and both values will exist in the BST.

思路

题目大意：在二分搜索树树上寻找两个节点的最近祖先，节点本身就是该节点的祖先。

做这道题一定要利用这棵树是二分搜索树的相关性质：即左子树的节点值小于根节点值，而右子树的节点值大于根节点值。那么如果两个节点分落在一个节点的左右子树，那么共同祖先只有一个，便是该点；如果两个节点在一个节点的同一个子树，那么判断是否其中一个节点是另一个节点的祖先；最后递归上述步骤。

代码

点击显/隐内容

class Solution:
    def lowestCommonAncestor(self, root, p, q):
        if root.val == p.val or root.val == q.val:
            return root
        if (root.val-q.val)*(root.val-p.val) <0:
            return root
        if root.val-q.val>0:
            return self.lowestCommonAncestor(root.left,p,q)
        else:
            return self.lowestCommonAncestor(root.right,p,q)

Symmetric Tree

题目

点击显/隐内容

Given a binary tree, check whether it is a mirror of itself (ie, symmetric around its center).

For example, this binary tree [1,2,2,3,4,4,3] is symmetric:

But the following [1,2,2,null,3,null,3] is not:

思路

题目大意：判断一棵树是否对称。

判断对称，以中间为中心，判断左右是否相同，但是我们判断的是节点值是否相等。可以发现，待判断的节点都是成对的：左子树的左节点 vs 右子树的右节点；左子树的右节点 vs 右子树的左节点。递归求解。

代码

点击显/隐内容

class Solution:
    def find(self,p,q):
        if not p and not q:
            return True
        if not p or not q:
            return False
        if p.val==q.val:
            return self.find(p.left,q.right) and self.find(p.right,q.left)
        else:
            return False
    def isSymmetric(self, root):
        """
        :type root: TreeNode
        :rtype: bool
        """
        if not root:return True
        return self.find(root.left,root.right)

Balanced Binary Tree

题目

点击显/隐内容

Given a binary tree, determine if it is height-balanced.

For this problem, a height-balanced binary tree is defined as:

a binary tree in which the depth of the two subtrees of every node never differ by more than 1.

Example 1:

Given the following tree [3,9,20,null,null,15,7]:

Return true.
Example 2:

Given the following tree [1,2,2,3,3,null,null,4,4]:

Return false.

思路

点击显/隐内容

题目大意：判断一棵树是否为平衡树，所谓平衡树，任意顶点的左右子树的高度相差不超过1。

那么根据平衡树的定义，首先判断根的左右子树是否满足定义；入室，则递归判断root的左子树和右子树。为了计算顶点的高度，我们需要引进高度计算函数。但是该方法的复杂度：

为了计算root的高度，我们需要从root遍历到leaf顶点，$O(n)$

为了计算左子树的高度，我们需要遍历一半的顶点，则计算左子树和右子树的复杂度$2O(\frac{1}{2})$

那么对于根的左子树，我们需要计算它的左右子树，各计算$\frac{1}{4}$的节点，时间是$O(\frac{1}{4})$，故对根的左子树的左右子树计算得总时间是$2O(\frac{1}{4})$；对于根的右子树，需要计算其左右子树，也需要$2O(\frac{1}{4})$时间；则总时间啊$4O(\frac{1}{4})$。

这样，算法的总时间是$O(nlogn)$。

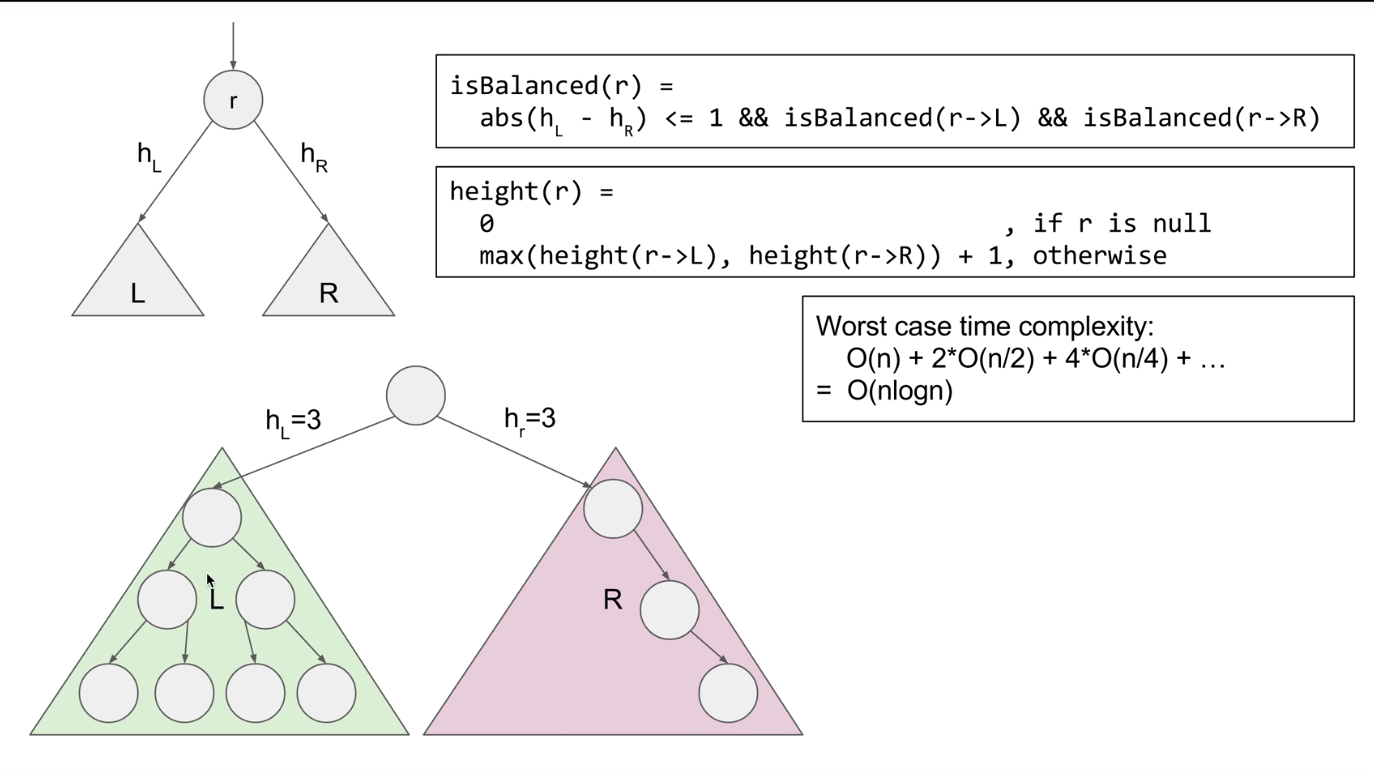
Screen Shot 2018-08-25 at 4.47.56 PM

仔细检查可以发现，我们有大量重复计算，左子树高度其实已经在计算root得高度时已经计算过了，实际上我们只需要遍历一次树就可以求出各顶点的高度。具体实现时，由于我们使用递归方法，在计算父亲节点之前，必然先求出孩子节点，所以，叶子节点的高度是最先求出来的，一旦求出后，我们马上比较它的左子树和右子树高度，如果大于1，则必然整棵树不是平衡树，返回-1。否则返回该节点的高度。所以，每次我们计算了节点高度后，先判断是否为-1，如果是，则返回，说明这棵树不是平衡树。

代码

点击显/隐内容

方法一：

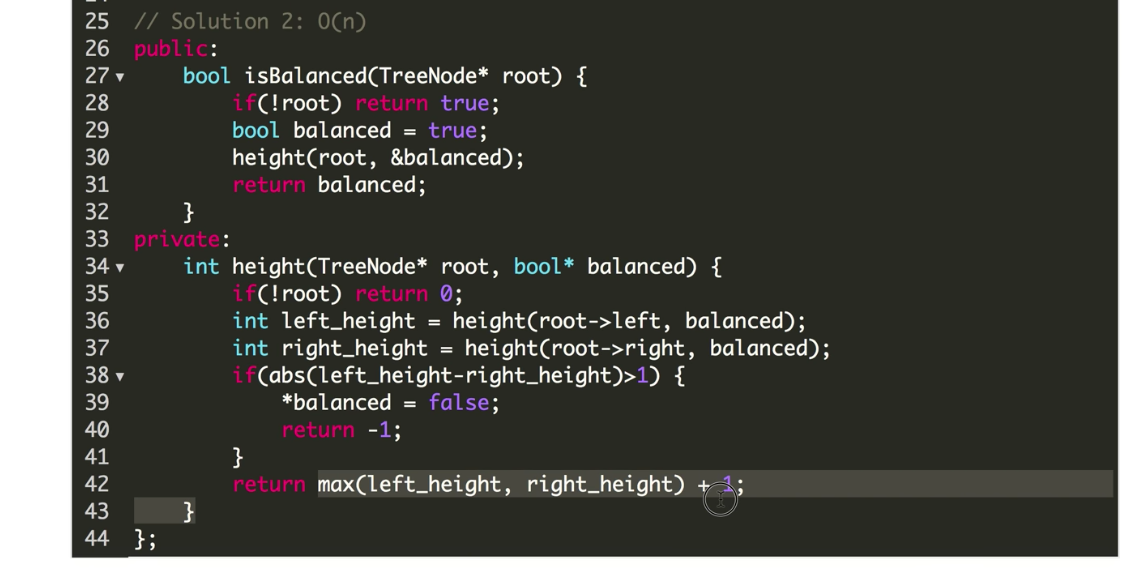
Screen Shot 2018-08-25 at 4.49.46 PM

方法二：

class Solution:
    def find_height(self,root):
        if not root:return 0
        l = self.find_height(root.left)
        if l==-1:return -1
        r = self.find_height(root.right)
        if r==-1:return -1
        if abs(l-r)>1:return -1
        return 1+max(l,r)
    def isBalanced(self, root):
        """
        :type root: TreeNode
        :rtype: bool
        """
        if not root:return True
        height = self.find_height(root)
        return False if height==-1 else True

Minimum Depth of Binary Tree

题目

点击显/隐内容

Given a binary tree, find its minimum depth.

The minimum depth is the number of nodes along the shortest path from the root node down to the nearest leaf node.

Note: A leaf is a node with no children.

Example:

Given binary tree [3,9,20,null,null,15,7],

return its minimum depth = 2.

思路

题目定义：求根到叶子的最短路径。

这道题完全是上一道题目Balanced Binary Tree的一部分，实质就是计算高度。求出根的左子树高度和右子树高度，选择小的那个；至于子树的高度，可以使用递归求解。但是有一点需要注意的是，求得是root到leaf的路径，如果给的树是如下，发现左子树高度是1，右子树高度是0，那么是不是应该选择右子树呢，答案为1呢？不，这样就不是一条从根到叶子的路径的。

1
2
3

 3
 / 
9

代码

点击显/隐内容

class Solution:
    def minDepth(self, root):
        """
        :type root: TreeNode
        :rtype: int
        """
        if not root:return 0
        if not root:return 0
        l = self.minDepth(root.left)
        r = self.minDepth(root.right)
        if min(l,r)==0:
            return l+r+1
        else:
            return 1+min(l,r)

困难

Path Sum III

题目

点击显/隐内容

ou are given a binary tree in which each node contains an integer value.

Find the number of paths that sum to a given value.

The path does not need to start or end at the root or a leaf, but it must go downwards (traveling only from parent nodes to child nodes).

The tree has no more than 1,000 nodes and the values are in the range -1,000,000 to 1,000,000.

Example:

root = [10,5,-3,3,2,null,11,3,-2,null,1], sum = 8

      10
     /  \
    5   -3
   / \    \
  3   2   11
 / \   \
3  -2   1

Return 3. The paths that sum to 8 are:

1.  5 -> 3
2.  5 -> 2 -> 1
3. -3 -> 11

思路

题目大意：在树上找到所有的路径，使每一条路径的和等于目标值，路径不要求从根开始，以叶子节点结束。

首先，我们使用一个额外函数来找到一条符合要求的路径：如果当前节点值等于目标值，则count+1；递归求解该节点的左右子树；

难点是如何求不以root开始的符合要求的路径？就是把每一个节点都当作root处理。

代码

点击显/隐内容

class Solution:
    def find(self,root,sum):
        if not root:return 0
        count = 0
        if root.val == sum:
            count += 1
        return count+self.find(root.left,sum-root.val)+self.find(root.right,sum-root.val)
    def pathSum(self, root, sum):
        if not root:return 0
        return self.find(root,sum) + self.pathSum(root.right,sum) + self.pathSum(root.left,sum)

Trim a Binary Search Tree

题目

点击显/隐内容

Given a binary search tree and the lowest and highest boundaries as L and R, trim the tree so that all its elements lies in [L, R] (R >= L). You might need to change the root of the tree, so the result should return the new root of the trimmed binary search tree.

Example 1:

Input: 
    1
   / \
  0   2

  L = 1
  R = 2

Output: 
    1
      \
       2

Example 2:

Input: 
    3
   / \
  0   4
   \
    2
   /
  1

  L = 1
  R = 3

Output: 
      3
     / 
   2   
  /
 1

思路

题目大意：给出一个取值区间范围，削减二分搜索树使该树上的节点值均介于该取值范围内。

首先一定要利用该树是二分搜索树的一些性质，左子树的节点值小于右子树的节点值。递归求解，对于每一个节点，如果该节点值小于L，那么该节点及其左子树便被削减，递归求解其右子树；如果该节点值大于R，则该节点及其右子树被削减，递归求解其左子树；如果该节点值在范围内，则递归求解左子树和右子树。

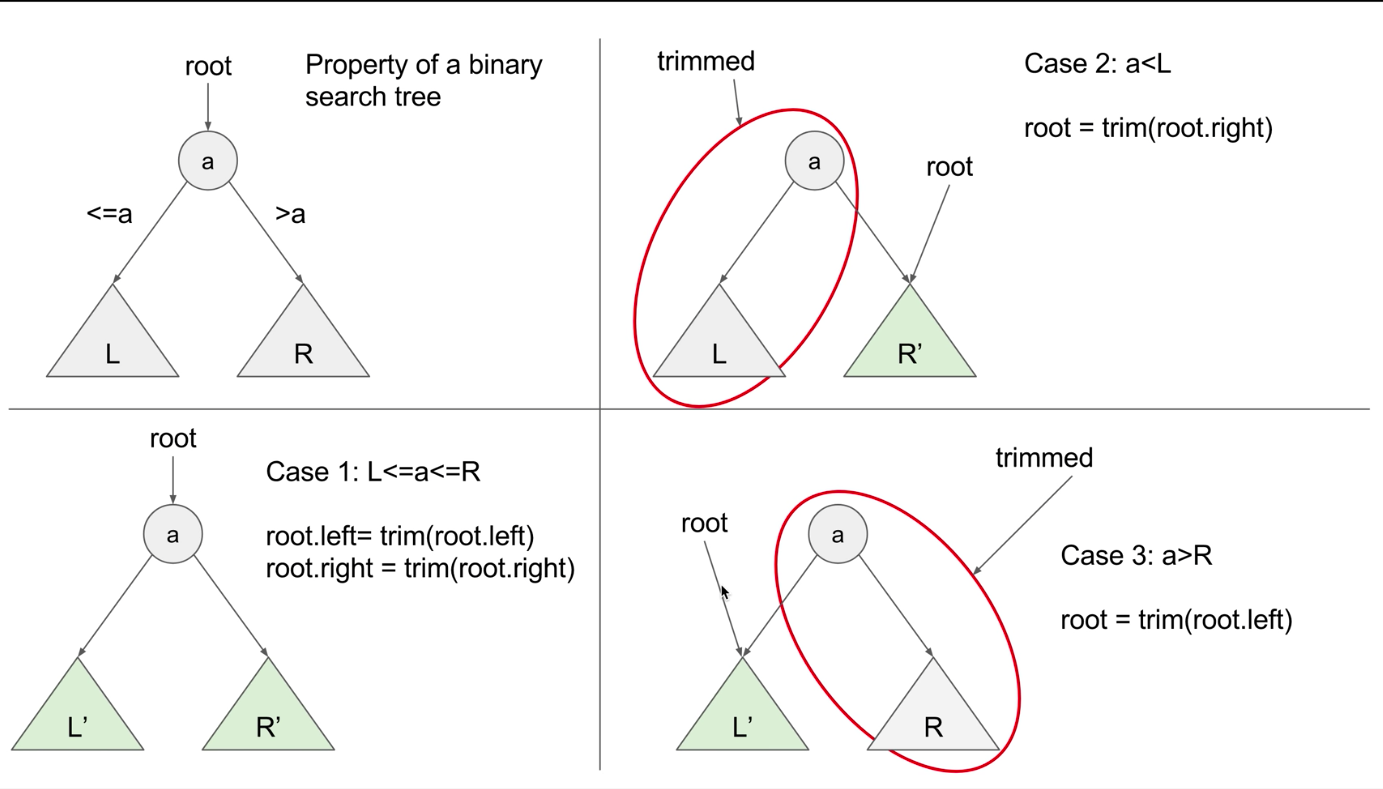
Screen Shot 2018-09-17 at 12.28.26 PM

代码

点击显/隐内容

class Solution:
    def trimBST(self, root, L, R):
        if not root:return None
        if root.val<L:
            return self.trimBST(root.right,L,R)
        if root.val>R:
            return self.trimBST(root.left,L,R)
        root.left = self.trimBST(root.left,L,R)
        root.right = self.trimBST(root.right,L,R)
        return root

Convert BST to Greater Tree

题目

点击显/隐内容

Given a Binary Search Tree (BST), convert it to a Greater Tree such that every key of the original BST is changed to the original key plus sum of all keys greater than the original key in BST.

Example:

Input: The root of a Binary Search Tree like this:
              5
            /   \
           2     13

Output: The root of a Greater Tree like this:
             18
            /   \
          20     13

思路

题目大意：对于搜索二叉树上每一个节点，更新其值为该节点与比该节点值大的所有节点值和。如题目给的例子，2是最小值，所以更新其值为2+5+13=20；对于5，比它大的只有13，更新5+13=18；又因为13是最大值，不更新。

这样最先处理最右的节点，然后不断累积sum和，我们使用中序遍历思想，但是先遍历右子树，然后是父节点，最后是左子树。

代码

点击显/隐内容

class Solution:
    def helper(self,root,tsum):   
        if root.right:
            root.right,tsum = self.helper(root.right,tsum)
        root.val += tsum
        tsum = root.val
        if root.left:
            root.left,tsum = self.helper(root.left,tsum)
        return root,tsum
    def convertBST(self, root):
        if not root:return root
        root,tsum = self.helper(root,0)
        return root

Diameter of Binary Tree

题目

点击显/隐内容

Given a binary tree, you need to compute the length of the diameter of the tree. The diameter of a binary tree is the length of the longest path between any two nodes in a tree. This path may or may not pass through the root.

Example:
Given a binary tree

Return 3, which is the length of the path [4,2,1,3] or [5,2,1,3].

Note: The length of path between two nodes is represented by the number of edges between them.

思路

题目大意：求二叉树的直径，直径的定义是树种最长路径。该直径可以不过root。

首先一看到不过root，就想到需要将左子树、右子树作为参数递归调用函数。那么问题就变成了如何求解一个点的最长路径？最长路径=左子树深度+右子树深度。那么问题就变成了如何求解树的深度。即如果树空，则深度为0；否则深度=max（左子树，右子树）+1。该种解法重复遍历树多次。

思路是那样，但是我们想控制时间复杂度在O(N)，我们设置一个全局变量diameter，每次处理一个节点时，将该节点的深度与diameter比较，更新。

代码

点击显/隐内容

class Solution:
    def bfs(self,root):
        if not root:return 0
        l = self.bfs(root.left)
        r = self.bfs(root.right)
        return max(l,r)+1
        
    def diameterOfBinaryTree(self, root):
        if not root:return 0
        cur = self.bfs(root.left)+self.bfs(root.right)
        cur_l = self.diameterOfBinaryTree(root.left)
        cur_r = self.diameterOfBinaryTree(root.right)
        cur_child = max(cur_l,cur_r)
        return max(cur,cur_child)

class Solution:
    def dfs(self,root):
            if not root:return 0
            l = self.dfs(root.left)
            r = self.dfs(root.right)
            if l+r>self.dia:
                self.dia = l+r
            return 1+max(l,r)     
    def diameterOfBinaryTree(self, root):
        self.dia = 0 
        self.dfs(root)
        return self.dia

Unique Binary Search Trees II

题目

点击显/隐内容

Given an integer n, generate all structurally unique BST’s (binary search trees) that store values 1 … n.

Example:

Input: 3
Output:
[
  [1,null,3,2],
  [3,2,null,1],
  [3,1,null,null,2],
  [2,1,3],
  [1,null,2,null,3]
]
Explanation:
The above output corresponds to the 5 unique BST's shown below:

   1         3     3      2      1
    \       /     /      / \      \
     3     2     1      1   3      2
    /     /       \                 \
   2     1         2                 3

All Possible Full Binary Trees

思路

代码

点击显/隐内容

class Solution:
    def helper(self,lis):
        n = len(lis)
        if n==0:return [None]
        if n==1:return [TreeNode(lis[0])]
        res = []
        for i in range(n):
            for j in self.helper(lis[:i]):
                for k in self.helper(lis[i+1:]):
                    root = TreeNode(lis[i])
                    root.left = j
                    root.right = k
                    res.append(root)
        return res
    def generateTrees(self, n):
        """
        :type n: int
        :rtype: List[TreeNode]
        """
        if n==0:return []
        lis = [i for i in range(1,n+1)]
        return self.helper(lis)