Array

简单

Move Zeros

题目 类似

Given an array nums, write a function to move all 0‘s to the end of it while maintaining the relative order of the non-zero elements.

Example:

Input: [0,1,0,3,12]
Output: [1,3,12,0,0]

Note:

1. You must do this in-place without making a copy of the array.
2. Minimize the total number of operations.

思路

题目大意：让我们将一个给定数组中所有的0都移到后面，把非零数前移，要求不能改变非零数的相对应的位置关系，而且不能拷贝额外的数组，那么只能用替换法in-place来做，需要用两个指针，一个不停的向后扫，找到非零位置，然后和前面那个指针交换位置即可

代码

class Solution {
public:
    void moveZeroes(vector<int>& nums) {
        int l = nums.size();
        for (int i=0,j=0;i<l;i++){
            if(nums[i]!=0){
                swap(nums[i],nums[j++]);
            }
        }
    }
};

Rotate Array

题目

Given an array, rotate the array to the right by k steps, where k is non-negative.

Example 1:

Input: [1,2,3,4,5,6,7] and k = 3
Output: [5,6,7,1,2,3,4]
Explanation:
rotate 1 steps to the right: [7,1,2,3,4,5,6]
rotate 2 steps to the right: [6,7,1,2,3,4,5]
rotate 3 steps to the right: [5,6,7,1,2,3,4]

Example 2:

Input: [-1,-100,3,99] and k = 2
Output: [3,99,-1,-100]
Explanation: 
rotate 1 steps to the right: [99,-1,-100,3]
rotate 2 steps to the right: [3,99,-1,-100]

Note:

• Try to come up as many solutions as you can, there are at least 3 different ways to solve this problem.
• Could you do it in-place with O(1) extra space?

思路

题目大意：以k为旋转点旋转数组。

为了防止k大于数组的长度，我们需要对k做取余操作。

法一：由于旋转数组的操作也可以看做从数组的末尾取k个数组放入数组的开头，所以我们用STL的push_back和erase可以很容易的实现这些操作。

法二：可以利用三次翻转操作，第一次全翻：7,6,5,4,3,2,1；第二次翻转k之前部分5,6,7||4,3,2,1；最后翻转k之后5,6,7||1,2,3,4

代码

//法一
class Solution {
public:
    void rotate(vector<int>& nums, int k) {
        int l = nums.size();
        k = k%l;
        for (int i=0;i<l-k;i++){
            nums.push_back(nums[0]);
            nums.erase(nums.begin());
        }
    }
};

//法二
class Solution {
public:
    void rotate(vector<int>& nums, int k) {
        k = k%nums.size();
        nums = helper(nums,0,nums.size()-1);
        nums = helper(nums,0,k-1);
        nums = helper(nums,k,nums.size()-1);        
        
    }
    public: vector<int> helper(vector<int>& nums, int s, int e){
        int mid = 0;
        while(s<e){
            mid = nums[s];
            nums[s] = nums[e];
            nums[e] = mid;
            s++;
            e--;
        }
        return nums;
    }
};

Pascal’s Triangle II

题目

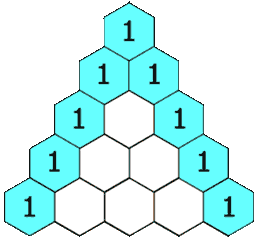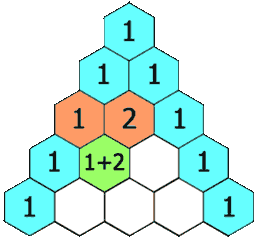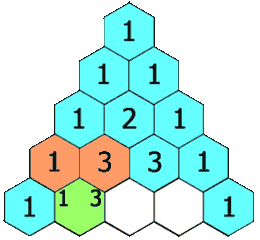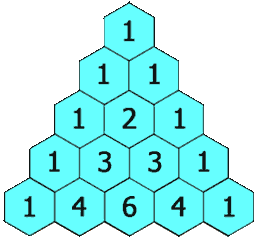
Given a non-negative index k where k ≤ 33, return the kth index row of the Pascal’s triangle.Note that the row index starts from 0.

Example:

Input: 3
Output: [1,3,3,1]

Follow up:

Could you optimize your algorithm to use only O(k) extra space?

思路

题目大意：返回Pascal三角的第k行。

第一种想法：借助一个二维数组，用来存储Pascal数列，这样空间复杂度是O(N*N)

第二种想法：借助一个一维动态数组，使用双重循环，外循环处理每一行，每次都插入一个1，内循环处理每一行的元素，则当前元素更新：nums[i]+=nums[i+1]

代码

class Solution {
public:
    vector<int> getRow(int rowIndex) {
        vector<vector<int>> pascal(rowIndex+1);
        if (rowIndex>=0){
            pascal[0] = vector<int>(1,1);
        }
        for(int i=1;i<=rowIndex;i++){
            vector<int> temp(i+1,1);
            for(int j=1;j<i;j++){
                temp[j]=pascal[i-1][j-1]+pascal[i-1][j];
            }
            pascal[i]=temp;
        }
        return pascal[rowIndex];
    }
};

class Solution {
public:
    vector<int> getRow(int rowIndex) {
        vector<int> res;
        for(int i=0;i<rowIndex+1;i++){
            res.insert(begin(res),1);
            for(int j=1;j<res.size()-1;j++){
                res[j]+=res[j+1];
            }
        }
        return res;
    }
};

Plus One

题目

Given a non-empty array of digits representing a non-negative integer, plus one to the integer.

The digits are stored such that the most significant digit is at the head of the list, and each element in the array contain a single digit.

You may assume the integer does not contain any leading zero, except the number 0 itself.

Example 1:

Input: [1,2,3]
Output: [1,2,4]
Explanation: The array represents the integer 123.

Example 2:

Input: [4,3,2,1]
Output: [4,3,2,2]
Explanation: The array represents the integer 4321.

思路

题目大意：一个整数的每一位被存在一个数组里，现在求该整数+1的结果。

主要的问题就是进位问题：如果该位小于9，那么该位+1，返回数组；否则，该位置空，处理下一位。最极端情况就是每一位都是9，那么数组全置空，增加一位，置1.

代码

class Solution {
public:
    vector<int> plusOne(vector<int>& digits) {
        int l = digits.size();
        for(int i=l-1;i>=0;i--){
            if(digits[i]<9){
                digits[i]++;
                return digits;
            }
            else{
                digits[i]=0;
            }
        }
        vector<int> res(l+1);
        res[0]=1;
        return res;
    }
};

Remove Duplicates from Sorted Array

题目

Given a sorted array nums, remove the duplicates in-place such that each element appear only once and return the new length.

Do not allocate extra space for another array, you must do this by modifying the input array in-place with O(1) extra memory.

Example 1:

Given nums = [1,1,2],

Your function should return length = 2, with the first two elements of nums being 1 and 2 respectively.

It doesn't matter what you leave beyond the returned length.

Example 2:

Given nums = [0,0,1,1,1,2,2,3,3,4],

Your function should return length = 5, with the first five elements of nums being modified to 0, 1, 2, 3, and 4 respectively.

It doesn't matter what values are set beyond the returned length.

Clarification:

Confused why the returned value is an integer but your answer is an array?

Note that the input array is passed in by reference, which means modification to the input array will be known to the caller as well.

Internally you can think of this:

// nums is passed in by reference. (i.e., without making a copy)
int len = removeDuplicates(nums);

// any modification to nums in your function would be known by the caller.
// using the length returned by your function, it prints the first len elements.
for (int i = 0; i < len; i++) {
    print(nums[i]);
}

思路

题目大意：将数组中存在的重复元素剔除，使每个元素只出现一次。要求直接在原数组上修改

代码

class Solution {
public:
    int removeDuplicates(vector<int>& nums) {
        int l = nums.size();
        if (l<1) return l;
        int count = 1;
        int ele = nums[0];
        for(int i=1;i<l;i++){
            if(ele!=nums[i]){
                ele=nums[i];
                nums[count++]=nums[i];
            }
        }
        return count;
    }
};

Merge Sorted Array

题目

Given two sorted integer arrays nums1 and nums2, merge nums2 into nums1 as one sorted array.

Note:

• The number of elements initialized in nums1 and nums2 are m and n respectively.
• You may assume that nums1 has enough space (size that is greater or equal to m + n) to hold additional elements from nums2.

Example:

Input:
nums1 = [1,2,3,0,0,0], m = 3
nums2 = [2,5,6],       n = 3

Output: [1,2,2,3,5,6]

思路

题目大意：将两个有序的数字合并成有序的数组，要求把合并的数组存在nums1中

最初的想法是设置一个辅助数组，两个指针分别指向两个数组，同时扫描比较，选择小的元素存在辅助数组中。但是这样空间复杂度是O(m+n)。

一个比较新颖的思路是：从后往前扫描，每次比较选择大的元素，这样直接存储在nums1中，根本不需要辅助数组。

代码

class Solution {
public:
    void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
        int cur = m+n-1;
        int pos1 = m-1;
        int pos2 = n-1;
        while(pos1>=0 && pos2>=0){
            if(nums1[pos1]>nums2[pos2]){
                nums1[cur--] = nums1[pos1--];
            }
            else{
                nums1[cur--] = nums2[pos2--];
            }
        }
        while(pos2>=0){
            nums1[cur--] = nums2[pos2--];
        }
    }
};

Missing Number

题目

Given an array containing n distinct numbers taken from 0, 1, 2, ..., n, find the one that is missing from the array.

Example 1:

Input: [3,0,1]
Output: 2

Example 2:

Input: [9,6,4,2,3,5,7,0,1]
Output: 8

Note:
Your algorithm should run in linear runtime complexity. Could you implement it using only constant extra space complexity?

思路

题目大意：找出0,1,2,...,n序列中缺失的一个数。

最开始的思路是借助一个map，数组中的值作为map的key，遍历完数组之后，遍历0-n，看看是否在map中存在。但是这样的空间复杂度是O(N)。

其实有两种做法：

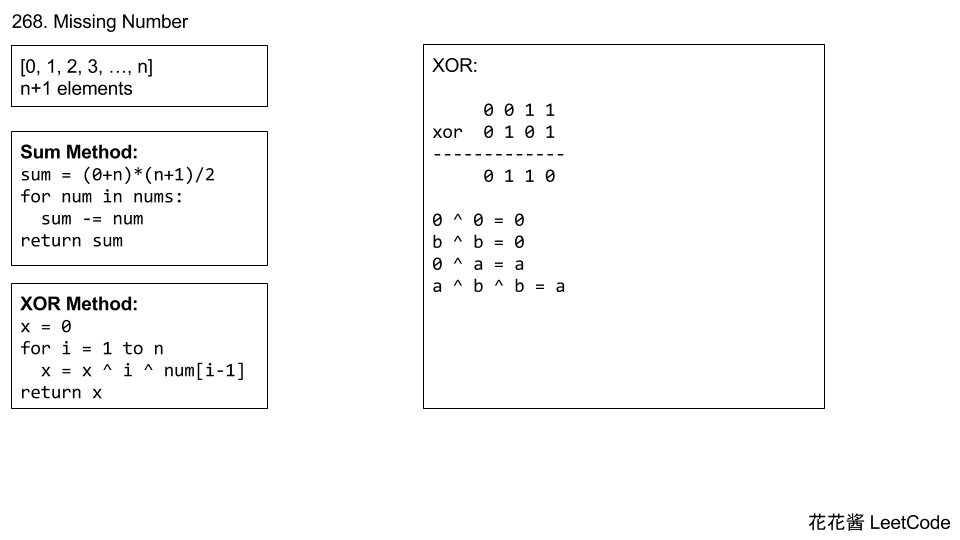
代码

class Solution {
public:
    int missingNumber(vector<int>& nums) {
        int l = nums.size();
        int sum_ = (1+l)*l/2;
        for (int i=0;i<l;i++){
            sum_ -= nums[i];
        }
        return sum_;
    }
};

class Solution {
public:
    int missingNumber(vector<int>& nums) {
        int l = nums.size();
        int res = 0;
        for (int i=0;i<l;i++){
            res = res^i^nums[i];
        }
        res = res^l;
        return res;
    }
};

Majority Elements

题目

Given an array of size n, find the majority element. The majority element is the element that appears more than ⌊ n/2 ⌋ times.

You may assume that the array is non-empty and the majority element always exist in the array.

Example 1:

Input: [3,2,3]
Output: 3

Example 2:

Input: [2,2,1,1,1,2,2]
Output: 2

思路

题目大意：数组中存在一个数，其出现的次数大于数组长度的一半，找出这个数。

用一种叫摩尔投票法 Moore Voting，需要O(n)的时间和O(1)的空间，比前一种方法更好。这种投票法先将第一个数字假设为众数，然后把计数器设为1，比较下一个数和此数是否相等，若相等则计数器加一，反之减一。然后看此时计数器的值，若为零，则将下一个值设为候选众数。以此类推直到遍历完整个数组，当前候选众数即为该数组的众数。不仔细弄懂摩尔投票法的精髓的话，过一阵子还是会忘记的，首先要明确的是这个叼炸天的方法是有前提的，就是数组中一定要有众数的存在才能使用，下面我们来看本算法的思路，这是一种先假设候选者，然后再进行验证的算法。我们现将数组中的第一个数假设为众数，然后进行统计其出现的次数，如果遇到同样的数，则计数器自增1，否则计数器自减1，如果计数器减到了0，则更换下一个数字为候选者。这是一个很巧妙的设定，也是本算法的精髓所在，为啥遇到不同的要计数器减1呢，为啥减到0了又要更换候选者呢？首先是有那个强大的前提存在，一定会有一个出现超过半数的数字存在，那么如果计数器减到0了话，说明目前不是候选者数字的个数已经跟候选者的出现个数相同了，那么这个候选者已经很weak，不一定能出现超过半数，我们选择更换当前的候选者。那有可能你会有疑问，那万一后面又大量的出现了之前的候选者怎么办，不需要担心，如果之前的候选者在后面大量出现的话，其又会重新变为候选者，直到最终验证成为正确的众数.

代码

class Solution {
public:
    int majorityElement(vector<int>& nums) {
        int count = 0;
        int res = 0;
        for(auto ele : nums){
            if (count==0){
                count++;
                res = ele;
            }
            else if(ele==res){
                count++;
            }
            else{
                count--;
            }
        }
        return res;
    }
};

Two Sum

类似题目：Contains Duplicate Contains Duplicate II

都是利用一个hash_table使在线性时间内完成。

题目

Given an array of integers, return indices of the two numbers such that they add up to a specific target.

You may assume that each input would have exactly one solution, and you may not use the same element twice.

Example:

Given nums = [2, 7, 11, 15], target = 9,

Because nums[0] + nums[1] = 2 + 7 = 9,
return [0, 1].

思路

题目大意：一个数组，还有一个目标数target，让我们找到两个数字，使其和为target。

为了提高时间的复杂度，需要用空间来换，这算是一个trade off吧，我们只想用线性的时间复杂度来解决问题，那么就是说只能遍历一个数字，那么另一个数字呢，我们可以事先将其存储起来，使用一个HashMap，来建立数字和其坐标位置之间的映射，我们都知道HashMap是常数级的查找效率，这样，我们在遍历数组的时候，用target减去遍历到的数字，就是另一个需要的数字了，直接在HashMap中查找其是否存在即可。

代码

class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        unordered_map<int,int> mymap;
        int l = nums.size();
        vector<int> res;
        int the_other = -1;
        for(int i=0;i<l;i++){
            the_other = target - nums[i];
            if (mymap.find(the_other) != mymap.end()){
                res.push_back(mymap[the_other]);
                res.push_back(i);
                break;
            }
            else{
                mymap[nums[i]] = i;
            }
        }
        return res;
    }
};

Third Maximum Number

题目

Given a non-empty array of integers, return the third maximum number in this array. If it does not exist, return the maximum number. The time complexity must be in O(n).

Example 1:

Input: [3, 2, 1]

Output: 1

Explanation: The third maximum is 1.

Example 2:

Input: [1, 2]

Output: 2

Explanation: The third maximum does not exist, so the maximum (2) is returned instead.

Example 3:

Input: [2, 2, 3, 1]

Output: 1

Explanation: Note that the third maximum here means the third maximum distinct number.
Both numbers with value 2 are both considered as second maximum.

思路

题目大意：求数组中第三大的数，如果不存在的话那么就返回最大的数。

用三个变量first, second, third来分别保存第一大，第二大，和第三大的数，然后我们遍历数组，如果遍历到的数字大于当前第一大的数first，那么三个变量各自错位赋值，如果当前数字大于second，小于first，那么就更新second和third，如果当前数字大于third，小于second，那就只更新third。

虽然这道题不难，但是实现的时候有诸多陷阱：初始化要用长整型long的最小值，否则当数组中有INT_MIN存在时，程序就不知道该返回INT_MIN还是最大值first了。其次，第三大不能和第二大相同，必须是严格的小于，而并非小于等于。即欲更新second，num[i]必须比first小。

代码

class Solution {
public:int thirdMax(vector<int>& nums) {
        int l = nums.size();
        long firstMax = LONG_MIN;
        long secondMax = LONG_MIN;
        long thirdMax = LONG_MIN;
        int cur = 0;
        for(int i=0;i<l;i++){
            cur = nums[i];
            if(cur>firstMax){
                thirdMax = secondMax;
                secondMax = firstMax;
                firstMax = cur;
            }
            else if(cur>secondMax&&cur!=firstMax){
                thirdMax = secondMax;
                secondMax = cur;
            }
            else if(cur>thirdMax&&cur!=firstMax&&cur!=secondMax){
                thirdMax = cur;
            }
        }
        return thirdMax==LONG_MIN?firstMax:thirdMax;
    }
};

Max Consecutive Ones

题目

Given a binary array, find the maximum number of consecutive 1s in this array.

Example 1:

Input: [1,1,0,1,1,1]
Output: 3
Explanation: The first two digits or the last three digits are consecutive 1s.
    The maximum number of consecutive 1s is 3.

Note:

• The input array will only contain 0 and 1.
• The length of input array is a positive integer and will not exceed 10,000

思路

题目大意：返回最长的连续1的长度。

两种思路：

一是遍历，记住连续1的起始index，每次遇到0，则更新。

二是遍历，使用count遍历记住连续1的个数，每次遇到0，则清空count。

代码

class Solution {
public:
    int findMaxConsecutiveOnes(vector<int>& nums) {
        nums.push_back(0);
        vector<int>::iterator it;
        it = nums.begin();
        it = nums.insert ( it , 0 );
        int start = 0;
        int l = nums.size();
        int res = 0;
        for (int i=0;i<l;i++){
            if (nums[i]==0){
                res = max(res,i-start-1);
                start = i;
            }
        }
        return res;
    }
};

class Solution {
public:
    int findMaxConsecutiveOnes(vector<int>& nums) {
        int l = nums.size();
        int res = 0;
        int count = 0;
        for (int i=0;i<l;i++){
            if (nums[i]==0){
                res = max(res,count);
                count = 0;
            }
            else{
                count++;
            }
        }
        return max(res,count); // for special input [1]
    }
};

中等

Number of Subarrays with Bounded Maximum

题目

We are given an array A of positive integers, and two positive integers L and R (L <= R).

Return the number of (contiguous, non-empty) subarrays such that the value of the maximum array element in that subarray is at least L and at most R.

Example :
Input: 
A = [2, 1, 4, 3]
L = 2
R = 3
Output: 3
Explanation: There are three subarrays that meet the requirements: [2], [2, 1], [3].

Note:

• L, R and A[i] will be an integer in the range [0, 10^9].
• The length of A will be in the range of [1, 50000].

思路

题目大意：找出所有可能的连续子数组，使该数组中的最大值在一个范围里面。

扫描一遍数组，当前的元素ele可能有三种情况：

1. $ele > R$: 那么该元素不能不能在子数组中，而且需要开始一个新的子数组。
2. $ele < L$: 那么该元素可以在子数组中，但是该元素与它前面的最近合法数字之间的元素不能单独成为子数组。
3. 否则，该元素是合法的。

实现的时候，我们使用两个指针：left=right=-1，left指针指向合法子数组的开始，right指向合法数组中最新的合法元素，即$L<ele<R$, 那么：

1. $ele > R$: 连续子数组被割断，则同时更新两个指针，left=right=idx
2. $ele < L$: 当前元素加入子数组，但是res += right-left
3. 否则：right=idx，res += right-left

代码

class Solution:
    def numSubarrayBoundedMax(self, A, L, R):
        res = 0
        left = -1
        right = -1
        for idx,ele in enumerate(A):
            if ele>R:
                left = idx
                right = idx
            elif ele<L:
                res += right-left #little number appended to the legitimate array
            else:
                right = idx
                res += right-left
        return res

Friends Of Appropriate Ages

题目

Some people will make friend requests. The list of their ages is given and ages[i] is the age of the ith person.

Person A will NOT friend request person B (B != A) if any of the following conditions are true:

• age[B] <= 0.5 * age[A] + 7
• age[B] > age[A]
• age[B] > 100 && age[A] < 100

Otherwise, A will friend request B.

Note that if A requests B, B does not necessarily request A. Also, people will not friend request themselves.

How many total friend requests are made?

Example 1:

Input: [16,16]
Output: 2
Explanation: 2 people friend request each other.

Example 2:

Input: [16,17,18]
Output: 2
Explanation: Friend requests are made 17 -> 16, 18 -> 17.

Example 3:

Input: [20,30,100,110,120]
Output: 
Explanation: Friend requests are made 110 -> 100, 120 -> 110, 120 -> 100.

Notes:

• 1 <= ages.length <= 20000.
• 1 <= ages[i] <= 120.

思路

题目大意：给出一个年龄列表，在满足条件下，求出最多的好友请求。

那就遍历一遍好友，对于每一个年龄，求出其可以发出的好友请求的年龄范围，然后加起来。

代码

from collections import Counter
class Solution:
    def numFriendRequests(self, ages):
        recorder = Counter(ages)
        res = 0
        for age in ages:
            recorder[age]-=1
            left,right = 8+age//2,age
            for i in range(left,right+1):
                res += recorder[i]
            recorder[age]+=1
        return res

Image Overlap

题目

Two images A and B are given, represented as binary, square matrices of the same size. (A binary matrix has only 0s and 1s as values.)

We translate one image however we choose (sliding it left, right, up, or down any number of units), and place it on top of the other image. After, the overlap of this translation is the number of positions that have a 1 in both images.

(Note also that a translation does not include any kind of rotation.)

What is the largest possible overlap?

Example 1:

Input: A = [[1,1,0],
            [0,1,0],
            [0,1,0]]
       B = [[0,0,0],
            [0,1,1],
            [0,0,1]]
Output: 3
Explanation: We slide A to right by 1 unit and down by 1 unit.

Notes:

1. 1 <= A.length = A[0].length = B.length = B[0].length <= 30
2. 0 <= A[i][j], B[i][j] <= 1

思路

题目大意：两张图片，使用01矩阵表示，通过移动一个矩阵(即上移，下移，左移和右移)，使最大化两个矩阵相应位置都是1，求出最大重合1的个数。

每一个矩阵的元素都与另一个矩阵中每一个元素求距离，即$(\Delta x,\Delta y)$，出现最多的$(\Delta x,\Delta y)$的个数就是结果。

代码

from collections import Counter
class Solution:
    def largestOverlap(self, A, B):
        row = len(A)
        col = len(A[0])
        mapping = []
        for i in range(row):
            for j in range(col):
                if A[i][j]:
                    for k in range(row):
                        for m in range(col):
                            if B[k][m]:
                                mapping.append((i-k,j-m))
        res = 0
        if mapping:
            c = Counter(mapping)
            res = c.most_common()[0][1]
        return res

Length of Longest Fibonacci Subsequence

题目

A sequence X_1, X_2, ..., X_n is fibonacci-like if:

• n >= 3
• X_i + X_{i+1} = X_{i+2} for all i + 2 <= n

Given a strictly increasing array A of positive integers forming a sequence, find the length of the longest fibonacci-like subsequence of A. If one does not exist, return 0.

(Recall that a subsequence is derived from another sequence A by deleting any number of elements (including none) from A, without changing the order of the remaining elements. For example, [3, 5, 8] is a subsequence of [3, 4, 5, 6, 7, 8].)

Example 1:

Input: [1,2,3,4,5,6,7,8]
Output: 5
Explanation:
The longest subsequence that is fibonacci-like: [1,2,3,5,8].

Example 2:

Input: [1,3,7,11,12,14,18]
Output: 3
Explanation:
The longest subsequence that is fibonacci-like:
[1,11,12], [3,11,14] or [7,11,18].

思路

代码

Best Time to Buy and Sell Stock

题目

Say you have an array for which the ith element is the price of a given stock on day i.

If you were only permitted to complete at most one transaction (i.e., buy one and sell one share of the stock), design an algorithm to find the maximum profit.

Note that you cannot sell a stock before you buy one.

Example 1:

Input: [7,1,5,3,6,4]
Output: 5
Explanation: Buy on day 2 (price = 1) and sell on day 5 (price = 6), profit = 6-1 = 5.
             Not 7-1 = 6, as selling price needs to be larger than buying price.

Example 2:

Input: [7,6,4,3,1]
Output: 0
Explanation: In this case, no transaction is done, i.e. max profit = 0.

思路

代码

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        
        int l = prices.size();
        if (l<1) return l;
        int min_ = prices[0];
        int res = 0;
        for(auto ele : prices){
            res = max(res,ele-min_);
            min_ = min(min_,ele);
        }
        return res;
    }
};

Maximum Subarray

题目

Given an integer array nums, find the contiguous subarray (containing at least one number) which has the largest sum and return its sum.

Example:

Input: [-2,1,-3,4,-1,2,1,-5,4],
Output: 6
Explanation: [4,-1,2,1] has the largest sum = 6.

思路

题目大意：找出连续和最大的子数组。

最初的思路是设置一个数组，存储每个元素可以累积的最大值，其值更新是max(nums[i],nums[i]+nums[i-1])。但是，这样空间复杂度是O(N)。

改进的想法是：

不要辅助数组，直接使用一个temp变量记录当前位置可以累积的最大值，temp=max(temp+nums[i],nums[i])；之所以可以这样做，是因为在辅助数组中，在更新的时候，我们只利用到当前元素的前一个元素。

代码

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int temp = nums[0];
        int sum_ = nums[0];
        int l = nums.size();
        for (int i=1;i<l;i++){
            temp = max(nums[i],temp+nums[i]);
            sum_ = max(sum_,temp);
        }
        return sum_;
    }
};

K-diff Pairs in an Array

题目

Given an array of integers and an integer k, you need to find the number of unique k-diff pairs in the array. Here a k-diff pair is defined as an integer pair (i, j), where i and j are both numbers in the array and their absolute difference is k.

Example 1:

Input: [3, 1, 4, 1, 5], k = 2
Output: 2
Explanation: There are two 2-diff pairs in the array, (1, 3) and (3, 5).
Although we have two 1s in the input, we should only return the number of unique pairs.

Example 2:

Input:[1, 2, 3, 4, 5], k = 1
Output: 4
Explanation: There are four 1-diff pairs in the array, (1, 2), (2, 3), (3, 4) and (4, 5).

Example 3:

Input: [1, 3, 1, 5, 4], k = 0
Output: 1
Explanation: There is one 0-diff pair in the array, (1, 1).

Note:

1. The pairs (i, j) and (j, i) count as the same pair.
2. The length of the array won’t exceed 10,000.
3. All the integers in the given input belong to the range: [-1e7, 1e7].

思路

题目大意：一个含有重复数字的无序数组，还有一个整数k，让我们找出有多少对不重复的数对(i, j)使得i和j的差刚好为k。

由于k有可能为0，而只有含有至少两个相同的数字才能形成数对，那么就是说我们需要统计数组中每个数字的个数。我们可以建立每个数字和其出现次数之间的映射，然后遍历哈希表中的数字，如果k为0且该数字出现的次数大于1，则结果res自增1；如果k不为0，且用当前数字加上k后得到的新数字也在数组中存在，则结果res自增1。需要注意的k不可能为负值。

代码

class Solution {
public:
    int findPairs(vector<int>& nums, int k) {
        unordered_map<int,int> mymap;
        for(auto ele : nums){
            mymap[ele]++;
        }
        int res = 0;
        if (k<0) return res;
        if (k==0){
            for(auto ele : mymap){
                if (ele.second>1)
                    res++;
            }
        }
        else{
            for(auto ele : mymap){
                if(mymap.find(ele.first+k) != mymap.end()){
                    res++;
                }
                    
            }
        }
        return res;
    }
};

Array Partition I

题目

Given an array of 2n integers, your task is to group these integers into n pairs of integer, say (a1, b1), (a2, b2), …, (an, bn) which makes sum of min(ai, bi) for all i from 1 to n as large as possible.

Example 1:

Input: [1,4,3,2]

Output: 4
Explanation: n is 2, and the maximum sum of pairs is 4 = min(1, 2) + min(3, 4).

Note:

1. n is a positive integer, which is in the range of [1, 10000].
2. All the integers in the array will be in the range of [-10000, 10000].

思路

题目大意：将长度为2n的数组分成n个长度为2的元组，使n个元组小值的和最大。

一个很直接的思路就是排序，然后遍历一遍，每次将偶数index上的值相加，这样的时间复杂度由排序控制是O(nlogn)。

但是，我们可以丢弃排序，增加一个数组，以空间换时间，将时间复杂度降维O(n)，空间复杂度为O(n)。

由题目看到，元素值范围是[-10000,10000]，这样我们设置一个长度为2*10000的数组，元素值为新数组的下标，新数组的值为下标在已知数组中出现的次数。第一次遍历nums，得到每个元素的频数，而且，隐含了排序。第二次遍历，如果新数组的值为0，则跳过；否则，判断是否为一对元素值得第一个；

代码

class Solution {
public:
    int arrayPairSum(vector<int>& nums) {
        const int max_val = 10000;
        vector<int> val_idx_map(2*max_val);
        for (auto ele : nums){
            val_idx_map[ele+max_val]++;
        }
        bool first = true;
        int n = -max_val;
        int res = 0;
        while(n<max_val){
            if (!val_idx_map[n+max_val]){
                n++;
                continue;
            }
            if (first){
                res += n;
                first = false;
            }else{
                first = true;
            }
            val_idx_map[n+max_val]--;
        }
        return res;
    }
};

Can Place Flowers

题目

Suppose you have a long flowerbed in which some of the plots are planted and some are not. However, flowers cannot be planted in adjacent plots - they would compete for water and both would die.

Given a flowerbed (represented as an array containing 0 and 1, where 0 means empty and 1 means not empty), and a number n, return if n new flowers can be planted in it without violating the no-adjacent-flowers rule.

Example 1:

Input: flowerbed = [1,0,0,0,1], n = 1
Output: True

Example 2:

Input: flowerbed = [1,0,0,0,1], n = 2
Output: False

Note:

1. The input array won’t violate no-adjacent-flowers rule.
2. The input array size is in the range of [1, 20000].
3. n is a non-negative integer which won’t exceed the input array size.

思路

题目大意：给定数组flowerbed表示一个花床，0表示位置为空，1表示位置非空。花不能相邻种植，即不能出现相邻的1。想要种植的花朵数目n，判断是否可以满足要求。

从左向右遍历flowerbed，将满足要求的0设为1。计数与n比较即可。

代码

class Solution {
public:
    bool canPlaceFlowers(vector<int>& flowerbed, int n) {
        int res = 0;
        int l = flowerbed.size();
        for (int i=0;i<l;i++){
            if (flowerbed[i]==1) continue;
            if (i>0 && flowerbed[i-1]==1) continue;
            if (i<l-1 && flowerbed[i+1]==1) continue;
            res ++;
            flowerbed[i] = 1;
        }
        if (res>=n)
            return true;
        else
            return false;
    }
};

Non-decreasing Array

题目

Given an array with n integers, your task is to check if it could become non-decreasing by modifying at most 1 element.

We define an array is non-decreasing if array[i] <= array[i + 1] holds for every i (1 <= i < n).

Example 1:

Input: [4,2,3]
Output: True
Explanation: You could modify the first 4 to 1 to get a non-decreasing array.

Example 2:

Input: [4,2,1]
Output: False
Explanation: You can't get a non-decreasing array by modify at most one element.

Note: The n belongs to [1, 10,000].

思路

代码

class Solution {
public:
    bool checkPossibility(vector<int>& nums) {
        int count = 0;
        int l = nums.size();
        for (int i=0;i<l-1;i++){
            if (nums[i]>nums[i+1]){
                count+=1;
                if(i==0){
                    nums[i]=nums[i+1]-1;
                }
                else if(nums[i-1]<nums[i+1]){ 
                    nums[i]=nums[i+1]-1;
                }
                else{
                    nums[i+1]=nums[i]+1;
                }
            }
                
            if (count>1)
                return false;
        }
        return true;
    }
};

1-bit and 2-bit Characters

题目

We have two special characters. The first character can be represented by one bit 0. The second character can be represented by two bits (10 or 11).

Now given a string represented by several bits. Return whether the last character must be a one-bit character or not. The given string will always end with a zero.

Example 1:

Input: 
bits = [1, 0, 0]
Output: True
Explanation: 
The only way to decode it is two-bit character and one-bit character. So the last character is one-bit character.

Example 2:

Input: 
bits = [1, 1, 1, 0]
Output: False
Explanation: 
The only way to decode it is two-bit character and two-bit character. So the last character is NOT one-bit character.

思路

题目大意：判断字符串是否只有10,11,0三个子串组成，而且以0结尾。

仔细分析之后，会发现如果字符以1开头，那么它只能是10或者11，如果是0开头，那么只能是0。基于此，我们扫描一遍字符串，如果当前字符是1，那么跳过下一个字符，直接扫描index = i+2的字符；如果当前字符是0，那么扫描下一个字符，判断是否能到达最后一个字符且为0。

代码

class Solution {
public:
    bool isOneBitCharacter(vector<int>& bits) {
        int l=bits.size();
        int i=0;
        while(i<l-1){
            if(bits[i]==0)
                i++;
            else
                i+=2;
        }
        if (i==(l-1) && bits[i]==0)
            return true;
        else
            return false;
    }
};

Find Pivot Index

题目

Given an array of integers nums, write a method that returns the “pivot” index of this array.

We define the pivot index as the index where the sum of the numbers to the left of the index is equal to the sum of the numbers to the right of the index.

If no such index exists, we should return -1. If there are multiple pivot indexes, you should return the left-most pivot index.

Example 1:

Input: 
nums = [1, 7, 3, 6, 5, 6]
Output: 3
Explanation: 
The sum of the numbers to the left of index 3 (nums[3] = 6) is equal to the sum of numbers to the right of index 3.
Also, 3 is the first index where this occurs.

Example 2:

Input: 
nums = [1, 2, 3]
Output: -1
Explanation: 
There is no index that satisfies the conditions in the problem statement.

思路

题目大意：在一数组中寻找一个点，使该点左边的元素和等于该点的右边元素和。

第一种方法是遍历每个点，然后分别计算点左边和，点右边和。但是这样的复杂度是$O(n)$.

第二中方法是同样遍历每个点，但是并不是每次都去计算左边和，右边和。实际上，每一次遍历的时候，左边和、右边和的差异就是当前点：即左边和=上一次的和+当前点，右边和=上一次的和-当前点。

代码

class Solution:
    def pivotIndex(self, nums):
        if not nums : return -1
        l = len(nums)
        lsum = 0
        rsum = sum(nums)
        for i in range(l):
            if (lsum==(rsum-nums[i])):
                return i
            lsum += nums[i]
            rsum -= nums[i]
        return -1

Largest Number At Least Twice of Others

题目

In a given integer array nums, there is always exactly one largest element.

Find whether the largest element in the array is at least twice as much as every other number in the array.

If it is, return the index of the largest element, otherwise return -1.

Example 1:

Input: nums = [3, 6, 1, 0]
Output: 1
Explanation: 6 is the largest integer, and for every other number in the array x,
6 is more than twice as big as x.  The index of value 6 is 1, so we return 1.

Example 2:

Input: nums = [1, 2, 3, 4]
Output: -1
Explanation: 4 isn't at least as big as twice the value of 3, so we return -1.

Note:

1. nums will have a length in the range [1, 50].
2. Every nums[i] will be an integer in the range [0, 99].

思路

题目大意：判断数组中最大数是否比剩下每个元素的两倍之大。

遍历一次，找出最大和次大的元素。重点是在次大元素的更新，每次最大元素更新，次大元素继承上一次最大元素值。

代码

class Solution:
    def dominantIndex(self, nums):
        if not nums:return -1
        res_index = 0
        highest = 0
        secondHighest = 0
        for idx,v in enumerate(nums):
            if highest<v:
                secondHighest = highest
                highest=v
                res_index = idx
            elif secondHighest<v:
                secondHighest = v
        if highest>=2*secondHighest:
            return res_index
        else:
            return -1

Toeplitz Matrix

题目

A matrix is Toeplitz if every diagonal from top-left to bottom-right has the same element.

Now given an M x N matrix, return True if and only if the matrix is Toeplitz.

Example 1:

Input:
matrix = [
  [1,2,3,4],
  [5,1,2,3],
  [9,5,1,2]
]
Output: True
Explanation:
In the above grid, the diagonals are:
"[9]", "[5, 5]", "[1, 1, 1]", "[2, 2, 2]", "[3, 3]", "[4]".
In each diagonal all elements are the same, so the answer is True.

Example 2:

Input:
matrix = [
  [1,2],
  [2,2]
]
Output: False
Explanation:
The diagonal "[1, 2]" has different elements.
**Note:**

1. matrix will be a 2D array of integers.
2. matrix will have a number of rows and columns in range [1, 20].
3. matrix[i][j] will be integers in range [0, 99].

思路

题目大意：判断一个矩阵所有对角线上的元素是否相等。

感觉挺巧的想法，遍历一遍矩阵，每次判断当前元素与其紧邻的对角线元素是否相等。

代码

class Solution {
public:
    bool isToeplitzMatrix(vector<vector<int>>& matrix) {
        int row = matrix.size();
        int col = matrix[0].size();
        for (int i=0;i<row-1;i++){
            for (int j=0;j<col-1;j++){
                if (matrix[i][j]!=matrix[i+1][j+1])
                    return false;
            }
        }
        return true;
    }
};

X of a Kind in a Deck of Cards

题目

In a deck of cards, each card has an integer written on it.

Return true if and only if you can choose X >= 2 such that it is possible to split the entire deck into 1 or more groups of cards, where:

• Each group has exactly X cards.
• All the cards in each group have the same integer.

Example 1:

Input: [1,2,3,4,4,3,2,1]
Output: true
Explanation: Possible partition [1,1],[2,2],[3,3],[4,4]

Example 2:

Input: [1,1,1,2,2,2,3,3]
Output: false
Explanation: No possible partition.

Example 3:

Input: [1]
Output: false
Explanation: No possible partition.

Example 4:

Input: [1,1]
Output: true
Explanation: Possible partition [1,1]

Example 5:

Input: [1,1,2,2,2,2]
Output: true
Explanation: Possible partition [1,1],[2,2],[2,2]

思路

题目大意：将数组划分成大小相同的组，每组元素相同且大小不小于2。

思路很直接，遍历数组，统计相同元素个数。只要最小组的长度大于2且是其他组的除数，就可以。但是，这个对例子[1,1,1,1,2,2,2,2,2,2]是不行的。实际上，只要各组长度之间存在大于1的最大公约数，该最大公倍数即最终划分的长度，则满足题意。

代码

class Solution {
public:
    bool hasGroupsSizeX(vector<int>& deck) {
        map<int,int> count;
        for (int i:deck){
            count[i] ++;
        }
        int min_count = 0;
        for (auto &v:count){
            if (min_count>v.second){
                min_count = v.second;
            }
        }
        for (auto &v:count){
            min_count = __gcd(min_count,v.second);
            if (min_count<2){
                return false;
            }
        }
        return true;
    }
};

Maximize Distance to Closest Person

题目

In a row of seats, 1 represents a person sitting in that seat, and 0 represents that the seat is empty.

There is at least one empty seat, and at least one person sitting.

Alex wants to sit in the seat such that the distance between him and the closest person to him is maximized.

Return that maximum distance to closest person.

Example 1:

Input: [1,0,0,0,1,0,1]
Output: 2
Explanation: 
If Alex sits in the second open seat (seats[2]), then the closest person has distance 2.
If Alex sits in any other open seat, the closest person has distance 1.
Thus, the maximum distance to the closest person is 2.

Example 2:

Input: [1,0,0,0]
Output: 3
Explanation: 
If Alex sits in the last seat, the closest person is 3 seats away.
This is the maximum distance possible, so the answer is 3.

Note:

1. 1 <= seats.length <= 20000
2. seats contains only 0s or 1s, at least one 0, and at least one 1.

思路

题目大意：给定一个0/1表示的座位数组，0表示空座位，1表示该位置有人。现要求找一个位置，使最大与旁边人的距离。

即对于每一个空座位，需要考虑左边最近人的距离和右边最近人的距离，那么该座位与旁人的最大距离为左右两边距离的较小一个。这样每一个空座位的最大距离求出之后，选择最大距离的座位。

为了求出每个座位与左右两边人的最近距离，我们使用遍历两次座位数组，第一次遍历求出空座位与周边人的距离；第二次遍历求出与右边人的距离。

代码

class Solution {
public:
    int maxDistToClosest(vector<int>& seats) {
        int pos = INT_MAX;
        vector<int> dis(seats.size(),INT_MAX);
        for (int i=0;i<seats.size();i++){
            if (seats[i]==1){
                pos = i;
                dis[i] = 0;
            }
            else{
                dis[i] = abs(pos-i);
            }
        }
        
        pos = INT_MAX;
        for (int i=seats.size()-1;i>-1;i--){
            if (seats[i]==1){
                pos = i;
            }
            else{
                dis[i] = min(abs(i-pos),dis[i]);
            }
        }
        auto maxPosition = max_element(dis.begin(), dis.end());
        return dis[maxPosition - dis.begin()];
        
    }
};