Clustering

聚类

在无监督学习中，训练样本的标记信息是未知的，目标是通过对无标记训练样本的学习来揭示数据内在性质及规律，此类学习中研究最多、应用最广的是“聚类(Clustering)”。

聚类试图将数据集中的样本划分为若干个不相交的子集，每个子集称为一个“簇(cluster)”。形式化地说，假定样本集$D=\{x_1,x_2,…,x_m\}$包含$m$个无标记的样本，每个样本$x_i=\{x_i^{1},x_i^{2},…,x_i^{n}\}$是一个$n$维特征向量，则聚类算法将$D$划分为$k$个不相交的簇。

K-means算法

模型

给定样本集$D=\{x_1,x_2,…,x_m\}$，“k均值”算法针对聚类所得到簇划分$C=\{C_1,C_2,…,C_k\}$最小化平方误差：

$$E=\sum_{i=1}^{k}\sum_{x\in C_i}||x-\mu_i||_{2}^{2}$$

其中，$u_i=\frac{1}{|C_i|}\sum_{x\in C_i}x$是簇$C_i$的均值向量。上式在一定程度上刻画了簇内样本围绕簇均值向量的紧密程度，E值越小则簇内样本相似度越高。

优缺点

1. Cons
   • 需要指定k值Selecting the number of clusters with silhouette analysis on KMeans clustering
   • 局限于线性边界的划分kernelized k-means
   • 数据量大时效率低

Python例子

K-means From Sratch

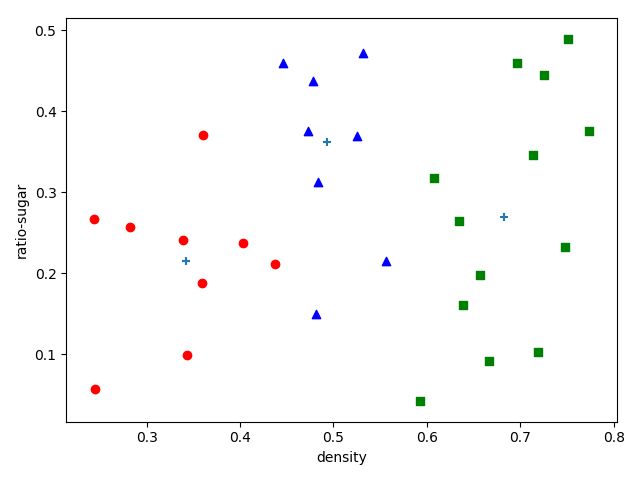
下面我们以一个例子来演示k均值算法的学习过程，数据如下所示：

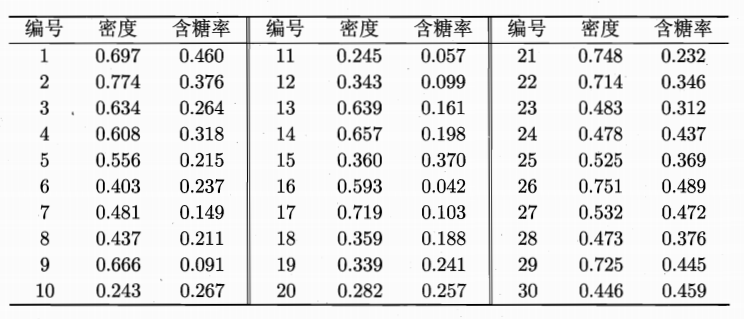
记第$i$个样本称为$x_i$，每个样本包含两个属性“密度”和“含糖率”，属于二值向量。

STEP1:数据读取。

我们使用panda的read_csv()函数读取.csv文件，header=None表示第一行也被读取。

def load_data(self):
    df = pd.read_csv(self.data_path,encoding = 'unicode_escape',header=None)
    self.data = df[[1,2]].values
    self.sample_num,self.attr_num = self.data.shape

STEP2:选取k个簇均值

这里我们k设置为3，随机从数据样本中选择3个样本作为初始簇均值向量。

def __init__(self):
    self.data_path = 'watermelon4_0.csv'
    self.cluster_center_change = True
    self.cluser_number = 3
    self.epoch = 10000
    self.load_data()

    #choose 3 random smaples as initial cluster centers
    idx = np.random.randint(self.sample_num,size=self.cluser_number)
    self.cluster_center = self.data[idx]

从上面看到，我们还设置了其他参数，如最大迭代次数10000，self.cluser_number就是k值。

STPE3:处理每一个样本

对每个样本，我们计算它与三个簇均值的欧氏距离，选择距离最小的簇作为该样本的归属簇。

#process each samples to find out the belonging cluster
for i,sample in enumerate(self.data):
    dis = []
    for j in range(self.cluser_number):
        dis.append(np.sqrt(np.sum(np.square(sample - self.cluster_center[j]))))
    label = dis.index(min(dis))
    clusters[label].append(i)

一旦处理完所有样本之后，我们就要更新每个簇的均值向量了。

#update the cluster center
for i in range(self.cluser_number):
    temp_cluster_center = sum(self.data[clusters[i]])/len(clusters[i])
    if any(self.cluster_center[i]-temp_cluster_center):
        self.cluster_center[i] = temp_cluster_center
self.cluster = clusters

组合在一起之后，我们的clustering更新如下：

def clustering(self):
    count = 0
    while count<self.epoch:
        count += 1
        clusters = []
        for i in range(self.cluser_number):
            clusters.append([])

        #process each samples to find out the belonging cluster
        for i,sample in enumerate(self.data):
            dis = []
            for j in range(self.cluser_number):
                dis.append(np.sqrt(np.sum(np.square(sample - self.cluster_center[j]))))
            label = dis.index(min(dis))
            clusters[label].append(i)

        #update the cluster center
        for i in range(self.cluser_number):
            temp_cluster_center = sum(self.data[clusters[i]])/len(clusters[i])
            if any(self.cluster_center[i]-temp_cluster_center):
                self.cluster_center[i] = temp_cluster_center
        self.cluster = clusters
        print("Done with the %d clustering"%count)

STEP4:每个簇内样本可视化

def visualize(self):
    x_axis = []
    y_axis = []
    for i in range(self.cluser_number):
        cluster_data = self.data[self.cluster[i]]
        tx_axis = []
        ty_axis = []
        for i in range(len(cluster_data)):
            tx_axis.append(cluster_data[i][0])
            ty_axis.append(cluster_data[i][1])
        x_axis.append(tx_axis)
        y_axis.append(ty_axis)
    cluster_center_x = []
    cluster_center_y = []
    for i in range(self.cluser_number):
        cluster_center_x.append(self.cluster_center[i][0])
        cluster_center_y.append(self.cluster_center[i][1])
    #plot cluster center
    plt.scatter(cluster_center_x,cluster_center_y,marker='+')
    plt.scatter(x_axis[0],y_axis[0],marker='o',c='red')
    plt.scatter(x_axis[1], y_axis[1], marker='s', c='green')
    plt.scatter(x_axis[2], y_axis[2], marker='^', c='blue')
    plt.xlabel('density')
    plt.ylabel('ratio-sugar')
    plt.show()

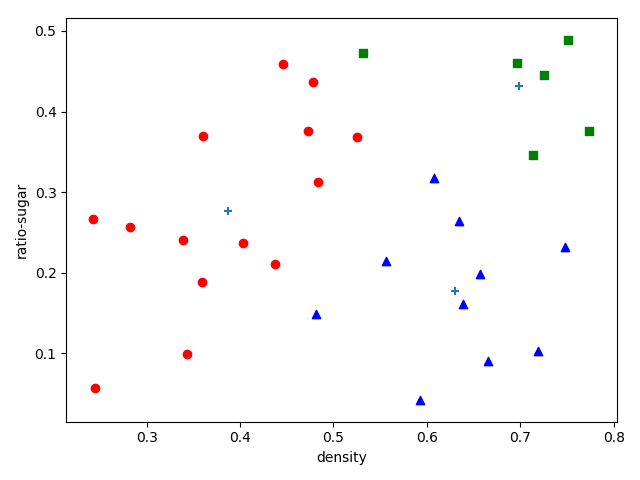
K-means in SKlearn

In Depth: k-Means Clustering

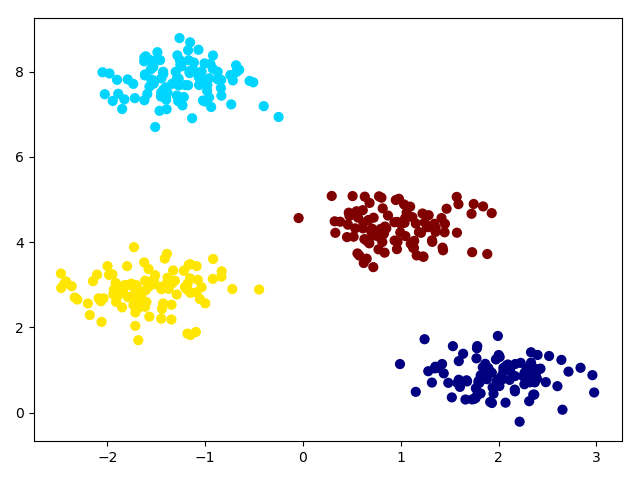
sklearn已经实现了k均值算法，我们直接使用它来解决问题。首先我们先生成4组二维无标签数据样本，

def sklearn(self):
    from sklearn.datasets.samples_generator import make_blobs
    x,y = make_blobs(n_samples=300,n_features=2,centers=4,cluster_std=0.6,random_state=0)
    plt.scatter(x[:,0],x[:,1],s=50)
    plt.show()

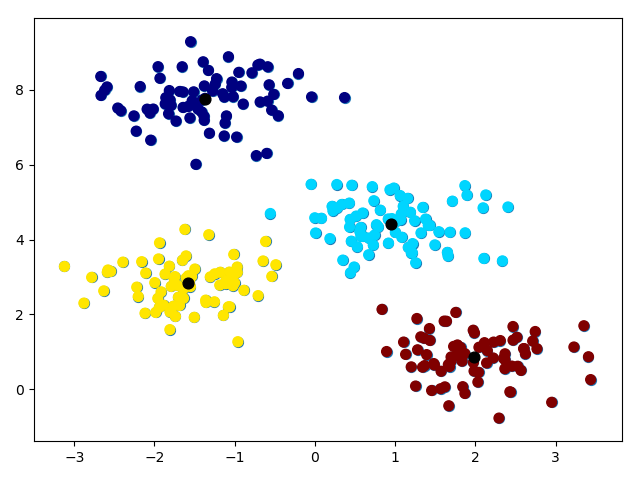
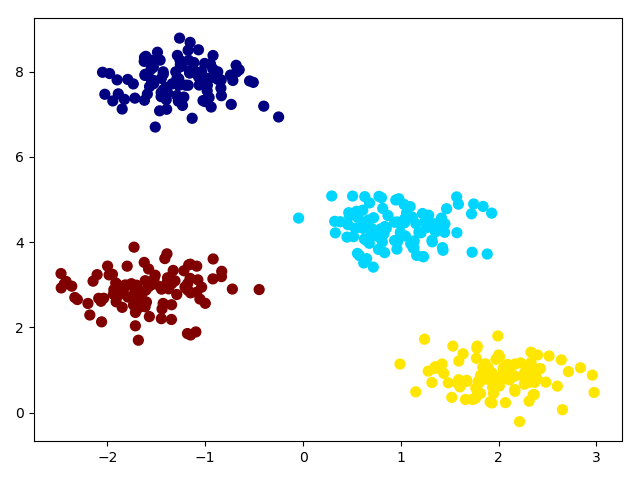
接下来，我们使用sklearn内置k-mean方法对上面的数据聚类

from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters=4)
kmeans.fit(x)
y_pre = kmeans.predict(x)
plt.scatter(x[:,0],x[:,1],c = y_pre,s=50,cmap='jet')

cluster_cenetr = kmeans.cluster_centers_
plt.scatter(cluster_cenetr[:,0],cluster_cenetr[:,1],c='k',s=60)
plt.show()

K-means in Digits Clustering

给定数字图，我们将它分为10个类。

首先我们载入数据，总共是1797个$8\times 8$的图片，这样每个样本就是64个特征。

def digits(self):
    from sklearn.datasets import load_digits
    digits = load_digits()
    from sklearn.cluster import KMeans
    kmeans = KMeans(n_clusters=10)
    y_pred = kmeans.fit_predict(digits.data)

    #可视化聚类中心
    clusters_center = kmeans.cluster_centers_.reshape([10,8,8])
    (fig,ax) = plt.subplots(2,5,figsize=(8,3))
    for i in range(2):
        for j in range(5):
            idx = (i+1)*(j+1)-1
            ax[i,j].imshow(clusters_center[idx])
    plt.show()

k-means for color compression

高斯混合聚类

k-means聚类属于hard assignments，即每一个点一定要被分配到一个类中；但是如果两个真实的簇相互重叠，在重叠区域的点可以同时属于两个类，但是k-means只会分配点到更近的簇中。而高斯混合模型聚类(Gaussian Mixture Models)解决这个问题。我们首先回顾高斯分布，然后介绍高斯混合模型，以及模型求解的方法EM算法。

一元高斯分布的密度函数为：

$$N(x;\mu, \sigma^2)=\frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x-u)^2}{2\sigma^2}}$$

多元高斯分布的密度函数：

一元高斯分布函数中的$x$是标量，多元高斯分布函数中的$x$是一个向量。

$$N(x;\mu,\sum)=\frac{1}{(2\pi)^{\frac{n}{2}}|\sum|^\frac{1}{2}}e^{\frac{1}{2}(x-u)^T}(\sum)^{-1}(x-u)$$

其中$\mu$是$n$维均值向量，$\sum$是$n\times n$的协方差矩阵。

模型

ref1 ref2 ref3 ref4 ref5

假设数据点来自几个不同的高斯分布，这样所有样本点混合一起，构成了一个高斯混合分布：

$$P_M(x)=\sum_{i=1}^{k}\alpha_i\cdotp(x|\mu_i,(\sum)_{i})$$

该分布共由$k$个混合分布组成，每个混合分布对应一个高斯分布，其中$u_i$与$\sum_i$是第$i$个高斯混合成分的参数，而$\alpha_i>0$为相应的混合系数，$\sum_{i=1}^{k}=1$。

假设样本的生成过程由高斯混合分布给出：首先，根据$\alpha_1, \alpha_2,…,\alpha_k$定义的先验分布选择高斯分布混合成分，其中$\alpha_i$为选择第$i$个混合成分的概率；然后，根据被选中的混合成分的概率密度函数进行采样，从而生成相应的样本。

Python例子

GMM from scratch

同样以上面的西瓜数据集为例，令高斯混合成分的个数$k=3$。算法开始时，假定高斯混合分布的模型参数初始化为：$\alpha_1=\alpha_2=\alpha_3=\frac{1}{3}$, $\sum_1=\sum_2=\sum_3=(\begin{matrix}0.1 & 0.0 \\0.0 & 0.1 \end{matrix})$ ， 随机选择$k$个样本点作为初始聚类中心。

def __init__(self):
    self.data_path = 'watermelon4_0.csv'
    self.cluster_center_change = True
    self.cluser_number = 3
    self.max_iter = 10000
    self.cluster = []
    self.load_data()

    # choose 3 random smaples as initial cluster centers
    idx = np.random.randint(self.sample_num, size=self.cluser_number)
    self.mean = self.data[idx]
    self.sigma = np.array([[[0.1,0],[0,0.1]],[[0.1,0],[0,0.1]],[[0.1,0],[0,0.1]]])
def load_data(self):
    df = pd.read_csv(self.data_path, encoding='unicode_escape', header=None)
    self.data = df[[1, 2]].values
    self.sample_num, self.attr_num = self.data.shape

根据多元高斯分布密度函数公式，我们完成密度函数计算：

$$N(x;\mu,\sum)=\frac{1}{(2\pi)^{\frac{n}{2}}|\sum|^\frac{1}{2}}e^{\frac{1}{2}(x-u)^T}(\sum)^{-1}(x-u)$$

def gaussian_pdf(self,x,u,sigma):
    n = np.shape(x)[0]
    expOn = -0.5*(x-u).dot(np.linalg.inv(sigma)).dot((x-u).T)
    divBy = (2*np.pi)**(n/2)*(np.linalg.det(sigma))**(.5)
    return pow(np.e,expOn)/divBy

E-step: 针对每个样本计算属于各个混合成分的概率

def clustering(self):
    self.alpha = [1/3,1/3,1/3]
    gamma = np.zeros((self.sample_num,self.cluser_number))
    iter = 0
    while (iter<self.max_iter):
        iter += 1
        # E step
        for i in range(self.sample_num):
            sumAlpha = 0
            for k in range(self.cluser_number): #for each sample, process the prob for each cluster
                gamma[i,k] = self.alpha[k]*self.gaussian_pdf(self.data[i],self.mean[k],self.sigma[k])
                sumAlpha += gamma[i,k]
            for k in range(self.cluser_number):
                gamma[i,k] /= sumAlpha
        sumGamma = np.sum(gamma,axis=0)

M-step: 更新高斯分布参数$u$和$\sum_i$, 以及混合系数$\alpha$

$$\mu_{i}^{'}=\frac{\sum_{j=1}^{m}\gamma_{ji}x_j}{\sum_{j=1}^{m}\gamma_{ji}} \\ {\sum}^{'}_{i}=\frac{\sum_{j=1}^{m}\gamma_{ji}(x_j-\mu_{i}^{'})(x_j-\mu_{i}^{'})^T}{\sum_{j=1}^{m}\gamma_{ji}}\\ \alpha_{i}^{'}=\frac{\sum_{j=1}^{m}\gamma_{ji}}{m}$$

for k in range(self.cluser_number):
    self.mean[k] = np.zeros((1,2))
    self.sigma[k] = np.zeros((2,2))
    for j in range(self.sample_num):
        self.mean[k] += gamma[j,k]*self.data[j]
    self.mean[k] = self.mean[k] / sumGamma[k]
    for j in range(self.sample_num):
        self.sigma[k] += gamma[j,k]*(self.data[j]-self.mean[k]).T*(self.data[j]-self.mean[k])
    self.sigma[k] /= sumGamma[k]
    self.alpha[k] = sumGamma[k]/self.sample_num
cluster = [[] for _ in range(self.cluser_number)]
for i in range(self.sample_num):
    maxP = list(gamma[i]).index(max(gamma[i]))
    cluster[maxP].append(i)
self.cluster = cluster

完整代码

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

 # 预处理数据
def loadData(filename):
    df = pd.read_csv('watermelon4_0.csv', encoding='unicode_escape', header=None)
    data = df[[1, 2]].values
    return data

 # 高斯分布的概率密度函数
def prob(x, mu, sigma):
     n = np.shape(x)[1]
     expOn = float(-0.5 * (x - mu) * (sigma.I) * ((x - mu).T))
     divBy = pow(2 * np.pi, n / 2) * pow(np.linalg.det(sigma), 0.5)  # np.linalg.det 计算矩阵的行列式
     # print(pow(np.e, expOn) / divBy)
     return pow(np.e, expOn) / divBy

 # EM算法
def EM(dataMat, maxIter=50):
     m, n = np.shape(dataMat)
     # 1.初始化各高斯混合成分参数
     alpha = [1 / 3, 1 / 3, 1 / 3]   # 1.1初始化 alpha1=alpha2=alpha3=1/3
     mu = [dataMat[5, :], dataMat[21, :], dataMat[26, :]] # 1.2初始化 mu1=x6,mu2=x22,mu3=x27
     sigma = [np.mat([[0.1, 0], [0, 0.1]]) for x in range(3)]    # 1.3初始化协方差矩阵
     gamma = np.mat(np.zeros((m, 3)))
     for i in range(maxIter):
         for j in range(m):
             sumAlphaMulP = 0
             for k in range(3):
                 gamma[j, k] = alpha[k] * prob(dataMat[j, :], mu[k], sigma[k]) # 4.计算混合成分生成的后验概率，即gamma
                 sumAlphaMulP += gamma[j, k]
             for k in range(3):
                 gamma[j, k] /= sumAlphaMulP
         sumGamma = np.sum(gamma, axis=0)
         # print(sumGamma)

         for k in range(3):
             mu[k] = np.mat(np.zeros((1, n)))
             sigma[k] = np.mat(np.zeros((n, n)))
             for j in range(m):
                 mu[k] += gamma[j, k] * dataMat[j, :]
             mu[k] /= sumGamma[0, k] #  7.计算新均值向量
             for j in range(m):
                 sigma[k] += gamma[j, k] * (dataMat[j, :] - mu[k]).T *(dataMat[j, :] - mu[k])
             sigma[k] /= sumGamma[0, k]  # 8. 计算新的协方差矩阵
             alpha[k] = sumGamma[0, k] / m   # 9. 计算新混合系数
             # print(mu)
     return gamma


 # init centroids with random samples
def initCentroids(dataMat, k):
     numSamples, dim = dataMat.shape
     centroids = np.zeros((k, dim))
     for i in range(k):
         index = int(np.random.uniform(0, numSamples))
         centroids[i, :] = dataMat[index, :]
     return centroids


def gaussianCluster(dataMat):
     m, n = np.shape(dataMat)
     centroids = initCentroids(dataMat, m)  ## step 1: init centroids
     clusterAssign = np.mat(np.zeros((m, 2)))
     gamma = EM(dataMat)
     for i in range(m):
         # amx返回矩阵最大值，argmax返回矩阵最大值所在下标
         clusterAssign[i, :] = np.argmax(gamma[i, :]), np.amax(gamma[i, :])  # 15.确定x的簇标记lambda
         ## step 4: update centroids
     for j in range(m):
         pointsInCluster = dataMat[np.nonzero(clusterAssign[:, 0].A == j)[0]]
         centroids[j, :] = np.mean(pointsInCluster, axis=0)  # 计算出均值向量
     return centroids, clusterAssign


def showCluster(dataMat, k, centroids, clusterAssment):
     numSamples, dim = dataMat.shape
     if dim != 2:
         print("Sorry! I can not draw because the dimension of your data is not 2!")
         return 1

     mark = ['or', 'ob', 'og', 'ok', '^r', '+r', 'sr', 'dr', '<r', 'pr']
     if k > len(mark):
         print("Sorry! Your k is too large!")
         return 1

         # draw all samples
     for i in range(numSamples):
         markIndex = int(clusterAssment[i, 0])
         plt.plot(dataMat[i, 0], dataMat[i, 1], mark[markIndex])

     mark = ['Dr', 'Db', 'Dg', 'Dk', '^b', '+b', 'sb', 'db', '<b', 'pb']
     # draw the centroids
     for i in range(k):
         plt.plot(centroids[i, 0], centroids[i, 1], mark[i], markersize=12)

     plt.show()

if __name__=="__main__":
     dataMat = np.mat(loadData('watermelon4.txt'))
     centroids, clusterAssign = gaussianCluster(dataMat)
     print(clusterAssign)
     showCluster(dataMat, 3, centroids, clusterAssign)

GMM in Sklearn

sklearn内置GMM算法，为了熟悉该方法，我们生成一组400个样本数据，隶属于4个簇：

def gmm(self):
    from sklearn.datasets.samples_generator import make_blobs
    x,y = make_blobs(n_samples=400,centers=4,cluster_std=0.4,random_state=0)
    from sklearn.mixture import GMM
    gmm = GMM(n_components=4).fit(x)
    lables = gmm.predict(x)
    plt.scatter(x[:,0],x[:,1],c=lables,s=40,cmap='jet')
    plt.show()

GMM给出了分类的置信度，predict_proba返回一个大小为[n_samples,n_clusters]的矩阵，每个元素值反应了样本点属于某个簇的概率大小。这样我们就可以将分类的不确定度可视化，通过使每个点的大小与分类确定度成正比。

def gmm(self):
    from sklearn.datasets.samples_generator import make_blobs
    x,y = make_blobs(n_samples=400,centers=4,cluster_std=0.4,random_state=0)
    from sklearn.mixture import GMM
    gmm = GMM(n_components=4).fit(x)
    lables = gmm.predict(x)
    prob = gmm.predict_proba(x)
    size = 50*(prob.max(1))**2
    plt.scatter(x[:,0],x[:,1],c=lables,s=size,cmap='jet')
    plt.show()

GMM as Density Estimation

除了聚类，高斯混合模型更常用于密度估计，即根据已知的数据样本去拟合该数据的分布，从而生成新的数据，这也使高斯混合模型成为一个生成模型。接下来我们生成一些数据样本，然后利用GMM去拟合该分布。

def density_estimation(self):
    from sklearn.datasets import make_moons
    x,y = make_moons(n_samples=200,noise=.05,random_state=0)
    plt.scatter(x[:,0],x[:,1],c=y,cmap='jet')
    plt.show()

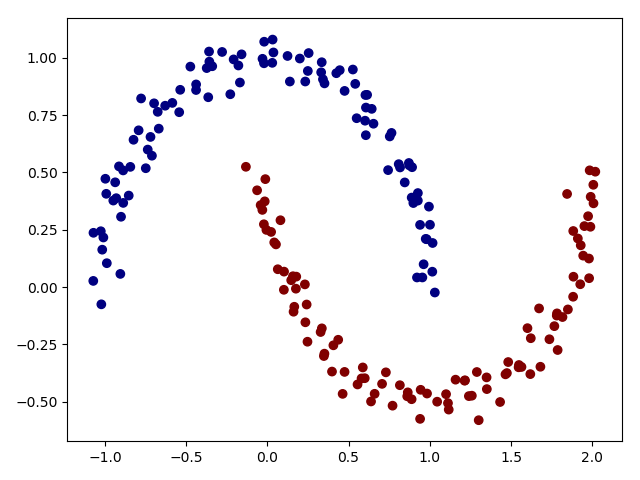
即我们生成的数据是2维度的，如果我们使用2成分的高斯混合模型去聚类：

def density_estimation(self):
    from sklearn.datasets import make_moons
    x,y = make_moons(n_samples=200,noise=.05,random_state=0)
    from sklearn.mixture import GMM
    gmm = GMM(n_components=2).fit(x)
    labels = gmm.predict(x)
    plt.scatter(x[:, 0], x[:, 1], c=labels, cmap='jet')
    plt.show()

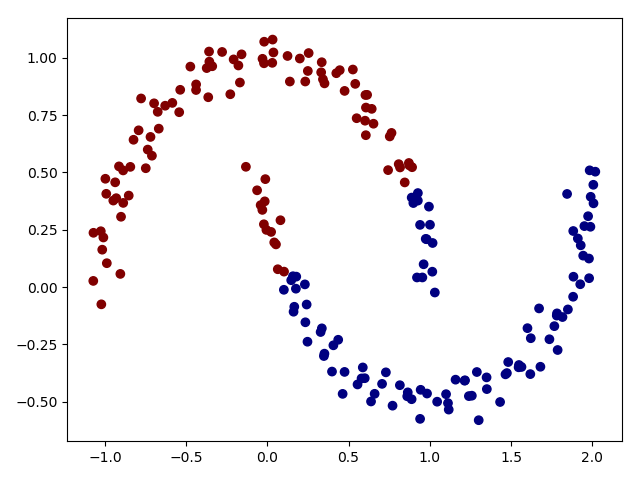
可以看到基于最近聚类的方法在这个例子中是不准确的，但是如果我们多增加几个成分，即成分个数变成16，gmm = GMM(n_components=16).fit(x)

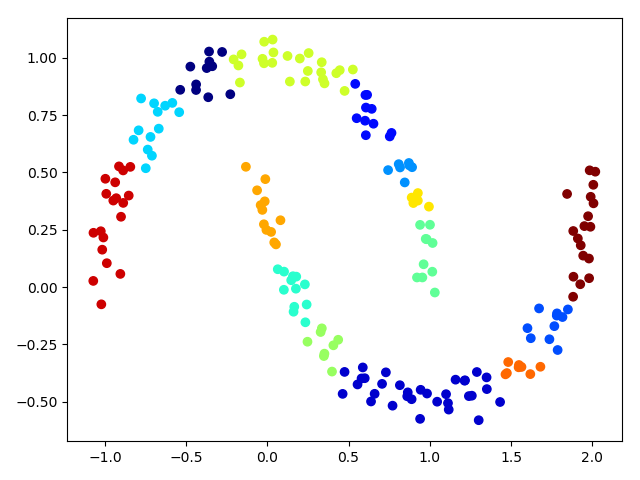
实际上，这16个高斯成分并不是用来数据划分，而是去建模数据整体分布。这是数据的生成模型，即GMM给了如何生成样本数据的模型，比如我们使用该模型去采样500个数据点：

def density_estimation(self):
    from sklearn.datasets import make_moons
    x,y = make_moons(n_samples=200,noise=.05,random_state=0)
    from sklearn.mixture import GMM
    gmm = GMM(n_components=16).fit(x)
    new_samples = gmm.sample(n_samples=400)
    plt.scatter(new_samples[:,0],new_samples[:,1])
    plt.show()

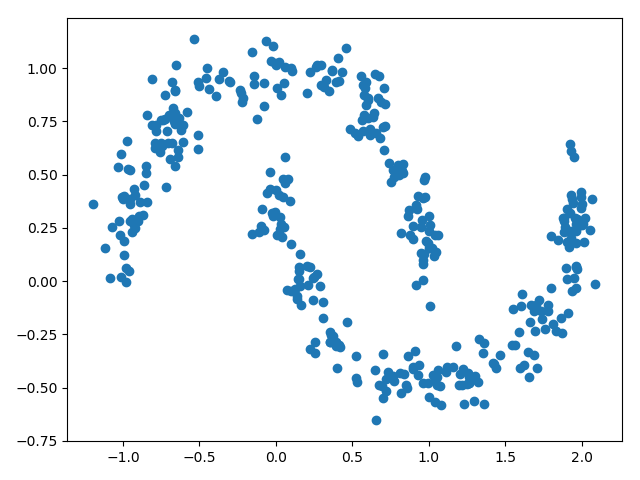
GMM in Data Generation

上面的例子简单地介绍了GMM在数据生成的应用，接下来我们介绍如何利用GMM 生成手写体数字。首先，我们先载入手写体数字：

def handwritten_estimation(self):
    from sklearn.datasets import load_digits
    (digits,target) = load_digits(return_X_y=True)

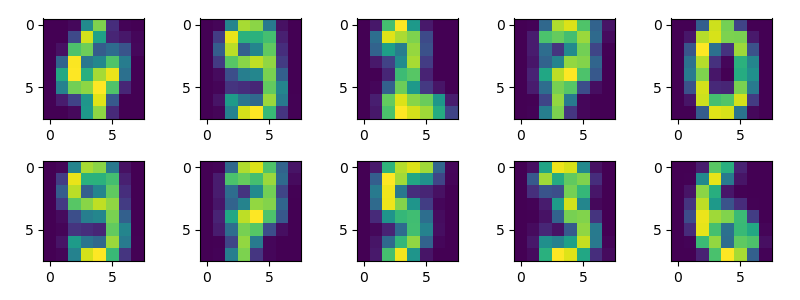
我们选取前100个数据进行可视化

def handwritten_estimation(self):
    from sklearn.datasets import load_digits
    (digits,target) = load_digits(return_X_y=True)
    def plot():
        fig,ax = plt.subplots(nrows=10,ncols=10,figsize=(8, 8),
                              subplot_kw=dict(xticks=[], yticks=[]))
        fig.subplots_adjust(hspace=0.05, wspace=0.05)
        for i in range(10):
            for j in range(10):
                img = digits[i*10+j].reshape(8,8)
                im = ax[i,j].imshow(img,cmap='binary') ## 图片可视化 imshow()
        plt.show()
    plot()

现在我们要使用GMM去拟合手写体，但是因为每一张图片的维度是64，对GMM而言，数据维度太高使模型不容易收敛，所以我们使用PCA进行降维。

from sklearn.decomposition import PCA
pca = PCA(0.99, whiten=True)
data = pca.fit_transform(digits) #data.shape = (1797, 41)

最终降维到41，几乎$\frac{1}{3}$无用的信息被去除。接下来我们使用AIC指标来指导我们如何选取最优的成分数目。

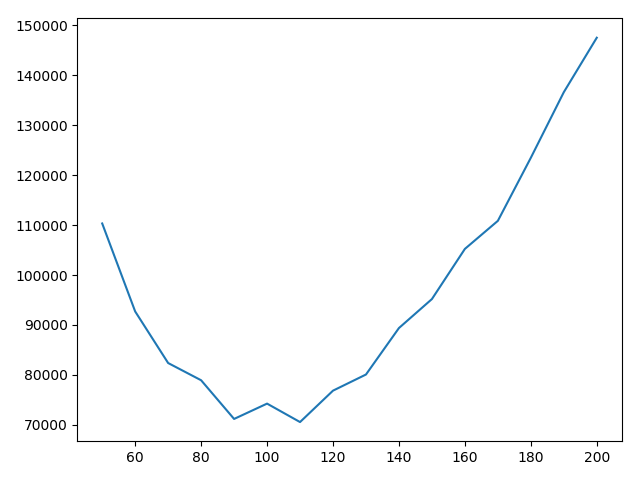
从图像中可以看到高斯成分数目为110是最佳的，所以：

gmm = GMM(110, covariance_type='full', random_state=0)
gmm.fit(data)
print(gmm.converged_) #true
data_new = gmm.sample(100, random_state=0) #data_new.shape=(100,41)
digits_new = pca.inverse_transform(data_new)
plot_digits(digits_new)
plt.show()