DP-Neural Network

Posted on | In

本节介绍最基本的神经网络。

神经网络

感知机模型

ref1 ref2

二分类线性模型

感知机作为一种二元线性分类模型，能（且一定能）将线性可分的数据集分开。什么叫线性可分？在二维平面上、线性可分意味着能用一条线将正负样本分开，在三维空间中、线性可分意味着能用一个平面将正负样本分开。

虽然简单，但它既可以发展成支持向量机（通过简单地修改损失函数），又可以发展为神经网络（通过简单地叠加），它的模型如下：

ikz

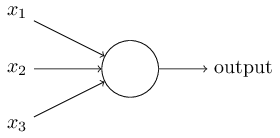
感知机接受几个输入$x_i$，对每一个权重赋予一个权重衡量该输入对输入的重要性，其输出为0或者1，由加权和$\sum_{j}{w_jx_j}$是否小于或者大于某一个阈值决定。和权重一样，阈值也是一个实数，同时它是神经元的一个参数。使用更严密的代数形式来表示：

以上为感知机的工作方式。鉴于上述表示方法过于繁琐，我们通过使用两个新记法来简化它。

第一个是使用点乘代替$\sum_{j}w_jx_j$：$w\cdot x \equiv \sum_{j}w_jx_j$

第二个是将阈值移到不等式的另一侧，并使用偏置(bias)来代替阈值：$bias \equiv -threshold$

如下图所示。

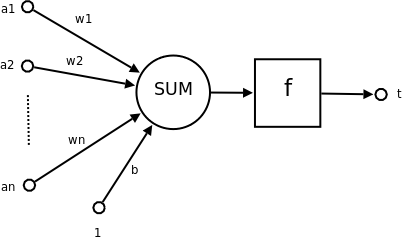
erceptron-027106

可以将偏置理解为感知机为了得到输出为1的容易度的度量，如果一个感知机的偏置非常大，那么这个感知机的输出很容易为1，相反如果偏置非常小，那么输出1就很困难。

感知机学习策略

为确定感知机模型参数$w$和$b$,需要定义一个损失函数并将损失函数最小化。样本点到超平面的距离:

$||w||$是$w$的$L_2$范数，为保计算结果为正，对$w\times x+b$进行绝对值运算。

对于误分类的数据$(x_i,y_i)$来说，$-y_i(w\times{x_i}+b)>0$，假设超平面$S$的误分类点集合为$M$，那么损失函数为所有误分类点到平面距离:

$$ L(w,b)=-\frac{1}{||w||}\sum_{x_i\in{M}}{{y_i(w\times{x_i}+b)}} $$ $\frac{1}{||w||}$是常量，不影响，$L(w,b)=-\sum_{x_i\in{M}}{{y_i(w\times{x_i}+b)}}$

采用梯度下降法，对于一个误分类样本点$(x_i,y_i)$，$\frac{\partial L}{\partial w}=-\eta{y_ix_i}$，$\frac{\partial{L}}{\partial{b}}=-\eta{y_i}$。

则参数更新公式为：

$w=w+\eta y_ix_i, b = b+\eta y_i$

逻辑计算

感知机可以用于计算初等逻辑函数：与、或、非。

$x_1$ $x_2$ AND OR NOT
0 0 0 0 1
0 1 0 1 1
1 0 0 1 0
1 1 1 1 0

感知机的输入是两个取值0、1的变量，

对于$AND$，它们对输出的贡献是相同的，则权重相同，我们取权重为-2和-2，但是发现4个里面才一个1，得到1比较困难，故有较高的阈值，设置阈值为3。

ikz

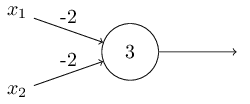
对于$OR$，权重相同，但是得到1比较容易，所以取较小的阈值，设置阈值为0.5。

对于$NOT$，发现只有一个输入，则只有一个输入对输出有影响，所以权重不同，$w_1=-1, w_2=0$，阈值为$-0.5$。

神经元模型

神经元和感知器本质上是一样的，只不过我们说感知器的时候，它的激活函数是阶跃函数；而当我们说神经元时，激活函数往往选择为sigmoid函数或tanh函数。

（1）M-P神经元模型：

神经元接收来自$n$个其他神经元传递过来的输入信号，这些输入信号通过待权重的连接进行传递，神经元接收到的总输入值将与神经元的阈值进行比较，然后通过”激活函数”处理以产生神经元的输出。

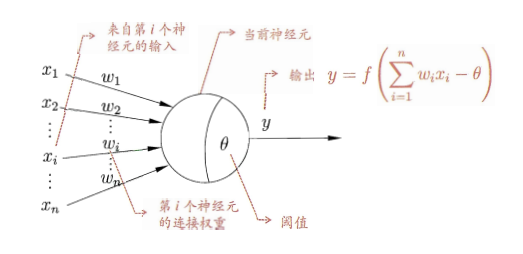
creen Shot 2018-08-23 at 8.45.15 P

（2）激活函数

采用（a）阶跃函数作为激活函数，它将输入值映射为输出值“1”（对应于神经元兴奋）或“0”（神经元抑制），可是阶跃函数不连续、不光滑，故采用sigmoid函数作为激活函数。

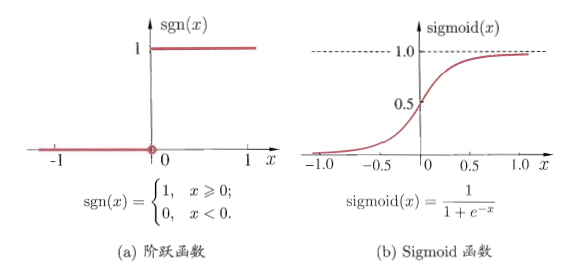
creen Shot 2018-08-23 at 8.46.24 P

故我们称上述神经元为sigmoid神经元。

感知机到sigmoid神经元的motivation：

We want a samll change in a weight (or bias) to cause a small change in output.

Compared to perceptron, both inputs and outputs of sigmoid neural can take on any values between 0 and 1 instead of just 0 or 1.

神经网络结构

多个sigmoid神经元构成复杂的神经网络。网络的最左边的一层被称为输入层，其中的神经元被称为输入神经元(input neurons)；最右边的一层是输出层(output layer)，包含的神经元被称为输出神经元(output neurons)。下图中我们的输出层只有一个神经元，网络的中间一层被称为隐层(hidden layer)，因为它既不是输入层，也不是输出层。

ikz1

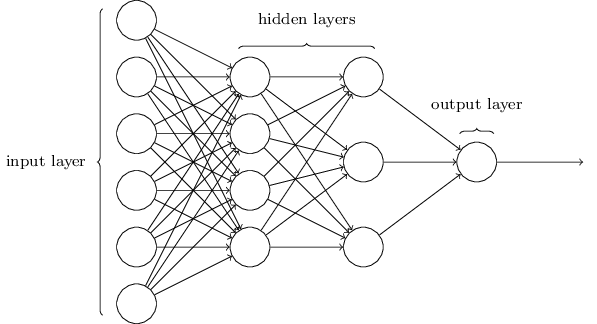
前向传播

ref1 ref2 gotta

神经网络的前向传播实质就是一个输入向量$\vec x$到输出向量$\vec y$的函数。下面我们使用一个例子来说明这个过程

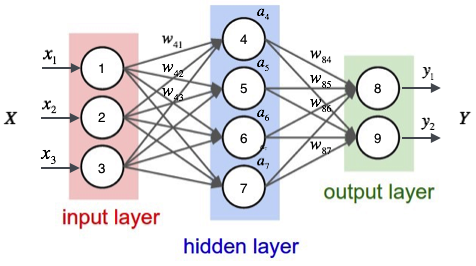
256672-bfbb364740f898d

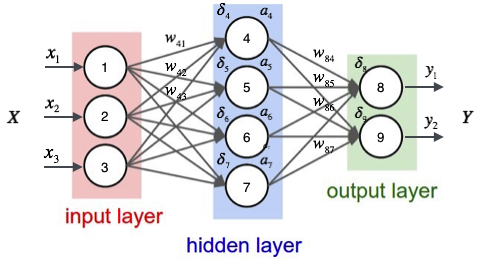
如上图，输入层有三个节点，我们将其依次编号为1、2、3；隐藏层的4个节点，编号依次为4、5、6、7；最后输出层的两个节点编号为8、9。因为我们这个神经网络是全连接网络，所以可以看到每个节点都和上一层的所有节点有连接。比如，我们可以看到隐藏层的节点4，它和输入层的三个节点1、2、3之间都有连接，其连接上的权重分别为$w_{41}, w_{42},w_{43}$。那么，我们怎样计算节点4的输出值$a_4$呢？

其中$w_{4b}$是节点4的偏置项，图中没有画出来。而$w_{41}, w_{42},w_{43}$分别为节点1、2、3到节点4连接的权重，在给权重编号时，我们把目标节点的编号$j$放在前面，把源节点的编号$i$放在后面。

同样，我们可以继续计算出节点5、6、7的输出值$a_5,a_6,a_7$。这样，隐藏层的4个节点的输出值就计算完成了，我们就可以接着计算输出层的节点8的输出值$y_1$：

同理，我们还可以计算出$y_2$的值。这样输出层所有节点的输出值计算完毕，我们就得到了在输入向量$\vec{x}=\begin{bmatrix}x_1\\x_2\\x_3\end{bmatrix}$时，神经网络的输出向量$\vec{y}=\begin{bmatrix}y_1\\y_2\end{bmatrix}$。这里我们也看到，输出向量的维度和输出层神经元个数相同。

神经网络的矩阵表示

神经网络的计算如果用矩阵来表示会很方便，我们先来看看隐藏层的矩阵表示。

首先我们把隐藏层4个节点的计算依次排列出来：

接着，定义网络的输入向量和隐藏层每个节点的权重向量$\vec w_j$，

代入得：

如果把$a_4,a_5,a_6,a_7$表示成一个矩阵，

代入得：

上式中，$f$是激活函数；$W$是某一层的权重矩阵；$\vec x$是某层的输入向量；$\vec a$是某层的输出向量。上式说明神经网络的每一层的作用实际上就是先将输入向量左乘一个数组进行线性变换，得到一个新的向量，然后再对这个向量逐元素应用一个激活函数。

每一层的算法都是一样的。比如，对于包含一个输入层，一个输出层和三个隐藏层的神经网络，我们假设其权重矩阵分别为$W_1, W_2,W_3,W_4$，每个隐藏层的输出分别是$\vec a_1, \vec a_2, \vec a_3$，神经网络的输入为$\vec x$，神经网络的输出为$\vec y$，如下图所示：

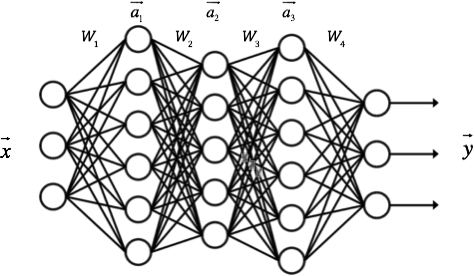
256672-c1388dc8fdcce42

则每一层的输出向量的计算可以表示为：

反向传播

现在，我们需要知道一个神经网络的每个连接上的权值是如何得到的。我们可以说神经网络是一个模型，那么这些权值就是模型的参数，也就是模型要学习的东西。然而，一个神经网络的连接方式、网络的层数、每层的节点数这些参数，则不是学习出来的，而是人为事先设置的。对于这些人为设置的参数，我们称之为超参数(Hyper-Parameters)。

接下来，我们将要介绍神经网络的训练算法：反向传播算法。

我们假设每个训练样本为$(\vec{x},\vec{t})$，其中向量$\vec x$是训练样本的特征，而$\vec t$是样本的目标值。

256672-6f27ced45cf5c0d

首先，我们根据前向传播算法，用样本的特征$\vec x$，计算出神经网络中每个隐藏层节点的输出$a_i$，以及输出层每个节点的输出$y_i$。

然后，我们按照下面的方法计算出每个节点的误差项$\delta_i$：

输出层

对于输出层的节点$i$

其中$\delta_i$是节点$i$的误差项，$y_i$是节点$i$的输出值，$t_i$是样本对应于节点$i$的目标值。比如：节点8的误差是$\delta_8=y_1(1-y_1)(t_1-y_1)$。

点击显/隐内容

按照机器学习的通用套路，我们先确定神经网络的目标函数，然后用随机梯度下降优化算法去求目标函数最小值时的参数值。

我们取网络所有输出层节点的误差平方和作为目标函数：

其中，$E_d$表示是样本$d$的误差，展开得到：

然后我们用随机梯度下降算法对目标函数进行优化：

随机梯度下降算法也就是需要求出误差对于每个权重的偏导数（也就是梯度），怎么求呢？

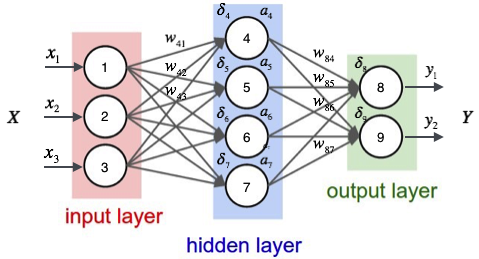
256672-6f27ced45cf5c0d8-551475

对于隐藏层与输出层间的权值，我们需要计算$\frac{\partial E_d}{\partial w_{ji} }$，由链式法则：

其中，$net_j$是是节点$j$的加权输入，即$ net_j=\vec{w_j}\centerdot\vec{x_j}=\sum_{i}{w_{ji}}x_{ji} $

$y_i$是激活函数处理之后的输出值。

考虑第一项：

考虑第二项：

source: Derivation: Derivatives for Common Neural Network Activation Functions

creen Shot 2019-02-13 at 10.26.59 A

将第一项和第二项带入，得到：

如果令$\sigma_j=\frac{\partial{E_d}}{\partial{net_j}}$来表示该节点的误差，则

将上述推导带入随机梯度下降公式，得到：

这样我们就得到了隐藏层权重的更新公式。

隐藏层

其中，$a_i$是节点的输出值，$w_{ki}$是节点$i$到它的下一层节点$k$的连接的权重，$\sigma_k$是节点$i$的下一层节点$k$的误差项。例如，对于隐藏层节点4来说，计算方法为：$\delta_4=a_4(1-a_4)(w_{84}\delta_8+w_{94}\delta_9)$

最后更新每个连接上的权值：

其中，$w_ji$是节点$i$到节点$j$的权重，$\eta$是学习速率，$\sigma_j$是节点$j$的误差项，$x_{ji}$是节点$i$传递给节点$j$的输入。例如，权重的更新方法如下：$w_{84}\gets w_{84}+\eta\delta_8 a_4$；类似的，权重$w_{41}$的更新方法如下：$w_{41}\gets w_{41}+\eta\delta_4 x_1$；

偏置项的输入值永远为1。例如，节点4的偏置项$w_{4b}$应该按照下面的方法计算： $w_{4b}\gets w_{4b}+\eta\delta_4$

显然，计算一个节点的误差项，需要先计算每个与其相连的下一层节点的误差项。这就要求误差项的计算顺序必须是从输出层开始，然后反向依次计算每个隐藏层的误差项，直到与输入层相连的那个隐藏层。这就是反向传播算法的名字的含义。

点击显/隐内容

同样地，我们需要计算$\frac{\partial E_d } {\partial w_{ji} }$,由链式法则：

考虑第一项：

首先，我们需要定义节点$j$的所有直接下游节点的集合$Downstream(j)$。例如，对于节点4来说，它的直接下游节点是节点8、节点9。可以看到$a_j$只能通过影响$Downstream(j)$再影响$E_d$。设$net_j$是节点$j$的下游节点的输入，则

考虑第二项：

综合第一项和第二项：

令$\delta_j=\frac{\partial E_d}{ \partial net_j }$，则

算法步骤

假设我们三层神经网络，即输入层、隐藏层和输出层，使用$L_2$损失函数。

  • 输入是x，令a1=x。
  • 前向传播
    • 输入层-隐藏层的前向传播：z2=a1*w1
    • 输入层-隐藏层的激活函数：a2=sigmoid(z2)
    • 隐藏层-输出层的前向传播：z3=a2*w2
    • 隐藏层-输出层的激活函数：h=sigmoid(z3)
  • 后向传播
    • 输出层-隐藏层的损失：h_err=(h-y)*sigmoid_prime(h)
    • 输出层-隐藏层的梯度：h_delta=h_err*a2
    • 隐藏层-输入层的损失：z2_err=(h_err*w2)*sigmoid_prime(a2)
    • 隐藏层-输入层的梯度：z2_delta=z2_err*a1
    • 更新梯度：w1 -= z2_delta,w2 -= h_delta

Python 实现

Toy Example

在该例子中，我们将建模一个具有二输入、一输出和一隐藏层的神经网络，该网络用于预测考试成绩基于两个输入：学习时间和睡觉时间。以下为训练样本：

学习时间 睡觉时间 考试成绩
2 9 92
1 5 86
3 6 89
4 8 ？

前向传播

考虑到时间是小时制，而考试成绩的百分制，所以我们想要将数据标准化，故对每一个变量我们都除以它的最大值。

1


2


3


4


5


import numpy as np


x = np.array(([2,9],[1,5],[3,6]),dtype=float)


y = np.array(([92],[86],[89]),dtype=float)


x = x/np.max(x,axis=0)


y = y/100

然后，我们定义一个类class和初始化函数init，在init函数中我们定义神经网络参数，如输入层，隐藏层和输出层。

1


2


3


4


5


6


7


class Neural_Network():


    def __init__(self):


        self.input_size = 2


        self.output_size = 1


        self.hidden_size = 3


        self.w1 = np.random.randn(self.hidden_size,self.input_size)


        self.w2 = np.random.randn(self.output_size,self.hidden_size)

变量定义好之后，我们便可以写前向传播函数了，在前向传播中，我们要完成的工作有输入与权重的点乘，再应用激活函数；隐层与权重的点乘，再应用一个激活函数得到输出。

1


2


3


4


5


6


def forward(self,x):


    self.z2 = x.dot(self.w1.T) # x.shape=(n,2) , w1.shape=(3,2),z1.shape=(n,3)


    self.a2 = self.sigmoid(self.z2)


    self.z3 = self.a2.dot(self.w2.T)


    o = self.sigmoid(self.z3)


    return o

所以，我们还需要定义一个sigmoid激活函数

1


2


def sigmoid(self,z):


    return 1/(1+np.exp(-z))

反向传播

第一步我们需要定义一个损失函数，我们使用MSE作为损失函数

其中，$o_i$是对$i_{th}$样本的预测，$y_i$是该样本的真实输出。

一旦定义好了损失函数，我们的目标就是使损失函数的值不断逼近0，即我们需要优化损失函数，我们需要激活函数的导数：

1


2


def sigmoid_prime(self,z):


    return z*(1-z)


1


2


3


4


5


6


7


8


9


def backward(self,x,y,o):


    self.o_err = o-y #shape=(n,output_size)


    self.o_delta = self.o_err*self.sigmoid_prime(o) #shape=(n,output_size)




    self.z2_err = self.o_delta.dot(self.w2) #(n,hidden_size)


    self.z2_delta = self.z2_err*self.sigmoid_prime(self.a2) #(n,hidden_size)




    self.w1 -= self.z2_delta.T.dot(x)


    self.w2 -= self.o_delta.T.dot(self.a2)

最后，我们便可以定义一个训练函数，它完成前向传播和后向传播

1


2


3


def train(self,x,y):


    o = self.forward(x)


    self.backward(x,y,o)

最后我们定义main函数，训练模型1000次

1


2


3


4


5


6


7


if __name__ == '__main__':


    nn = Neural_Network()


    for i in range(1000):


        o = nn.forward(x)


        # print("Predicted Output:",o)


        print("LOSS:",np.mean(np.square(y-o)))


        nn.train(x,y)

MNIST手写体数字分类

本例我们介绍如何使用神经网络进行多分类任务，数据集$ex3data1.mat$包含了5000个训练样本，每个样本都是$20\times 20$像素大小的灰度图片，这$20\times 20$大小的 图片被展开成一个400维的向量，也就是说，我们的训练数据集是一个$5000\times 400$的矩阵。同样地，图片的标签被记录在大小为5000维向量$y$里，范围从1-10。

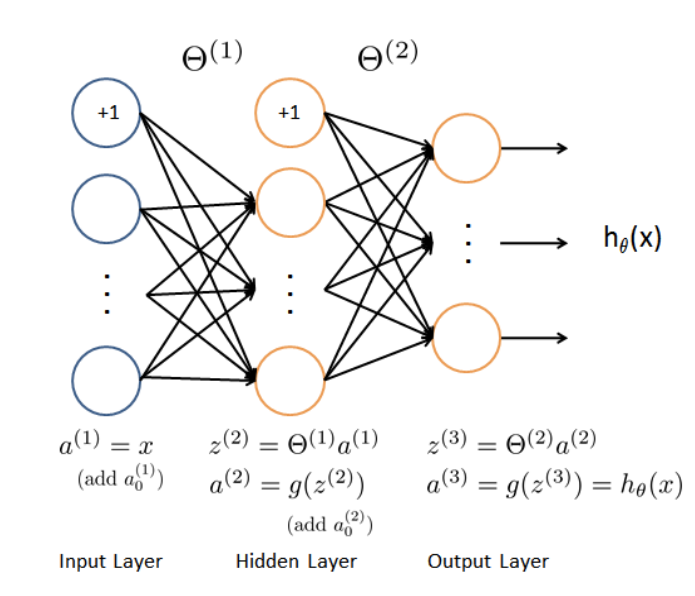
creen Shot 2018-08-29 at 10.22.09 P

我们就构建一个最简单的神经网络：输入层-隐藏层-输出层。

输入层神经元个数：$input_size=20\times 20 =400$

隐藏层神经元个数：$hidden_size=25$

输出层神经元个数：$output_size=10$

1


2


3


4


5


6


7


8


9


10


data = scipy.io.loadmat('dataset/ex3data1.mat')


x = data['X']


y = data['y']


encoder = OneHotEncoder(sparse=False)


y = encoder.fit_transform(y)




input_size = 400


hidden_size = 25


output_size = 10


learning_rate = 1

那么输入层和隐藏层之间的参数个数：$\theta_1=hidden_size \times (input_size+1)=25\times 401=10025$

输出层和隐藏层之间的参数个数：

$\theta_2=output_size \times (hidden_size+1)=10\times 26=260$

上式中的+1是偏置神经元。

所以这个神经网络的参数总数为：

$\theta=10025+260=10285$

1


2


3


4


5


theta = np.random.randn(hidden_size*(input_size+1)+output_size*(hidden_size+1))


theta1 = theta[0:hidden_size*(input_size+1)]


theta1 = theta1.reshape(hidden_size,input_size+1)


theta2 = theta[hidden_size*(input_size+1):]


theta2 = theta2.reshape(output_size,hidden_size+1)

不要将权重参数初始化为0

数据可视化

点击显/隐内容
1


2


3


4


5


6


7


8


9


10


11


12


13


14


15


16


17


18


19


20


21


22


23


24


25


26


27


28


29


30


31


32


33


def displayData(self,example_width=None, figsize=(10, 10)):


    """


    Displays 2D data stored in X in a nice grid.


    """


    # Compute rows, cols


    rand_indices = np.random.choice(len(self.y), 100, replace=False)


    X = self.x[rand_indices, :]


    if X.ndim == 2:


        m, n = X.shape


    elif X.ndim == 1:


        n = X.size


        m = 1


        X = X[None]  # Promote to a 2 dimensional array


    else:


        raise IndexError('Input X should be 1 or 2 dimensional.')




    example_width = example_width or int(np.round(np.sqrt(n)))




    # Compute number of items to display


    display_rows = int(np.floor(np.sqrt(m)))


    display_cols = int(np.ceil(m / display_rows))




    fig, ax_array = pyplot.subplots(display_rows, display_cols, figsize=figsize)


    fig.subplots_adjust(wspace=0.025, hspace=0.025)




    ax_array = [ax_array] if m == 1 else ax_array.ravel()




    for i, ax in enumerate(ax_array):


        # Display Image


        h = ax.imshow(X[i].reshape(example_width, example_width, order='F'),


                      cmap='Greys', extent=[0, 1, 0, 1])


        ax.axis('off')


    plt.show()

前向传播

输入是$x$，其维度是（$batch_size, 400$），我们需要对其插入一列全1偏置向量，得到新输入$a_1$变成（$batch_size, 401$）维：

1


2


row,col = np.shape


a1 = np.insert(x,np.ones(row),axis=1)

那么先全连接乘法，再对其使用激活函数：

$z_2=a1*theta1^T$

$a_2=sigmoid(z_2)$

1


2


z2 = a1.dot(theta1.T)


a2 = sigmoid(z2)

得到隐层输出$a_2$之后，我们计算输出层：

$a_2$的大小是（$batch_size,25$），我们需要插入偏置向量，变成$(batch_size,26)$

1


a2 = np.insert(a2,np.ones(row),axis=1)

$z_3=a2*theta2^T$

$ h=sigmoid(z_3)$

1


2


z3 = a2.dot(theta2.T)


h = sigmoid(z3)

这样我们就完成了前向传播的计算。

点击显/隐内容
1


2


3


4


5


6


7


8


9


10


11


12


13


14


def sigmoid(z):


    return 1/(1+np.exp(-z))


def forward_propagate(x,theta1,theta2):


    #x_shape = (5000,400)


    # theta1_shape = [hidden_size, input_size+1]


    # theta1_shape = [num_labels,hidden_size+1]


    row,col = np.shape(x)


    a1 = np.insert(x,0,np.ones(row),axis=1)


    z2 = a1.dot(theta1.T)


    a2 = sigmoid(z2)


    a2 = np.insert(a2,0,np.ones(row),axis=1)


    z3 = a2.dot(theta2.T)


    h = sigmoid(z3)


    return a1,z2,a2,z3,h

损失函数

我们利用神经网络进行分类任务，所以我们使用交叉熵来衡量损失：ref

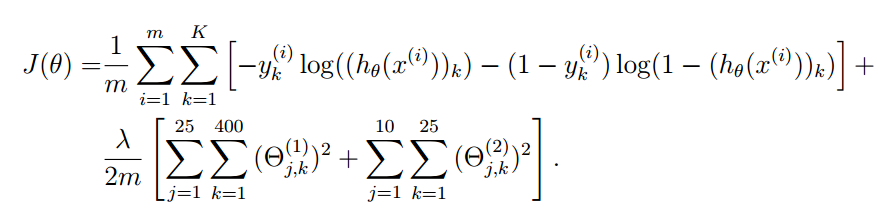
creen Shot 2018-09-02 at 4.03.40 P

上式是增加了正则化项的损失函数，其中$m$是样本数，即$batch_{size}$；$K$是输出神经元数，即$output_{size}$；$\lambda$是学习速率；需要注意的是，正则化项没有偏置参数。

why regularization

除了偏置神经元的权重之外，我们对网络的所有神经元的权重平方和作为正则化项。在求损失函数对权重的梯度时，在原来的梯度计算基础上，加上$\frac{\lambda}{m}\theta$。

回忆起$L_2$的梯度更新公式：

其中$L_2$的$\frac{\partial Cost}{\partial h}=(h-y)$，但是对于交叉熵而言$\frac{\partial Cost}{\partial h}=\frac{h-y}{h(1-h)}=\frac{h-y}{\sigma’(h)}$

$\frac{\partial Cost}{\partial h}$代入上式：

可以看出，偏导数是由$(h-y)$控制，模型的输出$h$与标签$y$之间的差异越大，偏导数就会越大，学习就会越快。

点击显/隐内容
1


2


3


4


5


6


7


8


9


10


11


12


def cost(thetas,x,y):


    row, col = np.shape(x)


    theta1 = thetas[:hidden_size*(input_size+1)].reshape(hidden_size,input_size+1)


    theta2 = thetas[hidden_size*(input_size+1   ):].reshape(num_labels,hidden_size+1)


    a1, z2, a2, z3, h = forward_propagate(x,theta1,theta2)


    # err = (h-y)**2


    # err = 0.5*sum(sum(err)/len(x))


    l1 = -y*(np.log(h))


    l2 = (y-1)*np.log(1-h)


    err = l1+l2


    reg_err = learning_rate/(2*row)*(np.sum(theta1[:,1:]**2)+np.sum(theta2[:,1:]**2))


    return np.mean(err)+reg_err,a1,z2,a2,z3,h

初始时，err=0.6383642819248599；reg_err=0.016015625000000002

反向传播

反向传播不断更新参数使样本的损失函数越来越小，不过我们需要一个工具计算激活函数的梯度：

其梯度为：

1


2


def sigmoid_gradient(z):


    return z*(1-z)

接下来我们需要逐层计算损失：

输出层损失：

$err_3=(a_3-y)*sigmoid_{gradient}(a_3)$，$shape=(batch_size,output_size)$

隐藏层与输出层之间的梯度：

1


z2 = np.insert(z2,0,np.ones(row),axis=1) #shape = (batch_size,hidden_size+1)

$\delta_3=[err_3]^T.*z_2$，$shape=(output_size,hidden_size+1)$

隐藏层损失：

$err_2=sigmoid_{gradient}(a_2)err_3. theta_2$,$shape=(batch_size,hidden_size+1)$

输入层与隐藏层之间的梯度：

$\delta_2=[err_2]^T.*a_1$，$shape=(hidden_size,input_size+1)$

KERAS版本实现

100epoch训练之后的正确率为94.56%。

点击显/隐内容
1


2


3


4


5


6


7


8


9


10


11


12


13


14


15


16


17


18


19


20


21


22


23


24


25


26


27


28


29


30


31


32


33


34


35


36


37


38


39


40


from keras.layers import Input, Dense


from keras.optimizers import Adam


from keras.models import Model


from scipy.io import loadmat


from sklearn.preprocessing import OneHotEncoder






class Ann():


    def __init__(self):


        self.input_size = 400


        self.hidden_size = 25


        self.output_size = 10




        opt = Adam(lr=0.0002,beta_1=0.5)




        self.ann = self.make_model()


        self.ann.compile(loss='categorical_crossentropy',


                         optimizer=opt,


                         metrics=['accuracy'])




    def make_model(self):


        inputs = Input((self.input_size,))


        h = Dense(self.hidden_size,activation='sigmoid')(inputs)


        outputs = Dense(self.output_size,activation='sigmoid')(h)


        model = Model(inputs,outputs)


        model.summary()


        return model




    def train(self):


        data = loadmat('dataset/ex3data1.mat')


        X = data['X']


        y = data['y']


        encoder = OneHotEncoder(sparse=False)


        y = encoder.fit_transform(y)




        results = self.ann.fit(X,y,epochs=100)




if __name__ == '__main__':


    ann = Ann()


    ann.train()

梯度检查

实现了神经网络的前向传播和后向传播之后，为保证我们的代码能正确运行，在进行神经网络训练数据之前，我们需要检查梯度是否正确。最简单的方法是将神经网络的梯度与我们手工计算得梯度进行比较。

也就是说，反向传播计算出来的梯度应该近似上述式子计算出来的梯度，否则我们的代码有误。

一般的，我们设置$\epsilon=10^{-7}$，而两个梯度之间的差异应该小于$10^{-7}$。

  1. 神经网络中容易被忽视的基础知识

Numpy Implementation

点击显/隐内容
1


2


3


4


5


6


7


8


9


10


11


12


13


14


15


16


17


18


19


20


21


22


23


24


25


26


27


28


29


30


31


32


33


34


35


36


37


38


39


40


41


42


43


44


45


46


47


48


49


50


51


52


53


54


55


56


57


58


59


60


61


62


63


64


65


66


67


68


69


70


71


72


73


74


75


76


77


78


79


80


81


82


83


84


85


86


87


88


89


90


91


92


93


94


95


96


97


98


99


100


101


102


103


104


105


106


107


108


109


110


111


112


113


114


115


116


117


118


119


120


121


122


123


124


125


126


127


128


129


130


131


132


133


134


135


136


137


138


139


140


141


142


143


144


145


146


147


148


149


150


151


152


153


154


155


156


157


158


159


160


161


162


163


164


165


166


167


168


169


170


171


172


173


174


175


176


177


178


179


180


181


182


183


184


185


186


187


188


import numpy as np




class TwoLayersNetwork():


    def __init__(self,input_size, hidden_size, output_size, std=1e-4):


        """


        Initialize the model. Weights are initialized to small random values and


        biases are initialized to zero. Weights and biases are stored in the


        variable self.params, which is a dictionary with the following keys:




        W1: First layer weights; has shape (D, H)


        b1: First layer biases; has shape (H,)


        W2: Second layer weights; has shape (H, C)


        b2: Second layer biases; has shape (C,)




        Inputs:


        - input_size: The dimension D of the input data.


        - hidden_size: The number of neurons H in the hidden layer.


        - output_size: The number of classes C.


        """


        self.params = {}


        self.params['W1'] = std * np.random.randn(input_size, hidden_size)


        self.params['b1'] = np.zeros(hidden_size)


        self.params['W2'] = std * np.random.randn(hidden_size, output_size)


        self.params['b2'] = np.zeros(output_size)




    def loss(self, X, y=None, reg=0.0):


        """


        Compute the loss and gradients for a two layer fully connected neural


        network.




        Inputs:


        - X: Input data of shape (N, D). Each X[i] is a training sample.


        - y: Vector of training labels. y[i] is the label for X[i], and each y[i] is


          an integer in the range 0 <= y[i] < C. This parameter is optional; if it


          is not passed then we only return scores, and if it is passed then we


          instead return the loss and gradients.


        - reg: Regularization strength.


        - relu activation function




        Returns:


        If y is None, return a matrix scores of shape (N, C) where scores[i, c] is


        the score for class c on input X[i].




        If y is not None, instead return a tuple of:


        - loss: Loss (data loss and regularization loss) for this batch of training


          samples.


        - grads: Dictionary mapping parameter names to gradients of those parameters


          with respect to the loss function; has the same keys as self.params.


        """


        # Unpack variables from the params dictionary


        W1, b1 = self.params['W1'], self.params['b1']


        W2, b2 = self.params['W2'], self.params['b2']


        N, D = X.shape




        # Compute the forward pass


        scores = None




        s1 = X.dot(W1) + b1


        a1 = np.maximum(s1, 0)


        scores = a1.dot(W2) + b2




        # If the targets are not given then jump out, we're done


        if y is None:


            return scores




        # Compute the loss




        normalized_scores = scores - np.max(scores, axis=1).reshape((-1, 1))


        exp_scores = np.exp(normalized_scores)


        soft_scores = exp_scores / (np.sum(exp_scores, axis=1).reshape((-1, 1)))


        target_scores = soft_scores[np.arange(N), y]


        loss = -1 * np.sum(np.log(target_scores)) / N + reg * (np.sum(W1 ** 2) + np.sum(W2 ** 2))






        # Backward pass: compute gradients


        grads = {}




        dSoftmax = soft_scores


        dSoftmax[np.arange(N), y] -= 1


        dW2 = a1.T.dot(dSoftmax)


        db2 = np.sum(dSoftmax, axis=0)




        dRelu = np.zeros_like(a1)


        dRelu[a1 > 0] = 1




        prev = dSoftmax.dot(W2.T)


        prev *= dRelu




        dW1 = X.T.dot(prev)


        db1 = np.sum(prev, axis=0)




        grads['W2'] = dW2 / N + 2 * reg * W2


        grads['b2'] = db2 / N


        grads['W1'] = dW1 / N + 2 * reg * W1


        grads['b1'] = db1 / N




        return loss, grads




    def train(self, X, y, X_val, y_val,


              learning_rate=1e-3, learning_rate_decay=0.95,


              reg=5e-6, num_iters=100,


              batch_size=200, verbose=False):


        """


        Train this neural network using stochastic gradient descent.




        Inputs:


        - X: A numpy array of shape (N, D) giving training data.


        - y: A numpy array f shape (N,) giving training labels; y[i] = c means that


          X[i] has label c, where 0 <= c < C.


        - X_val: A numpy array of shape (N_val, D) giving validation data.


        - y_val: A numpy array of shape (N_val,) giving validation labels.


        - learning_rate: Scalar giving learning rate for optimization.


        - learning_rate_decay: Scalar giving factor used to decay the learning rate


          after each epoch.


        - reg: Scalar giving regularization strength.


        - num_iters: Number of steps to take when optimizing.


        - batch_size: Number of training examples to use per step.


        - verbose: boolean; if true print progress during optimization.


        """


        num_train = X.shape[0]


        iterations_per_epoch = max(num_train / batch_size, 1)




        N, D = X.shape




        # Use SGD to optimize the parameters in self.model


        loss_history = []


        train_acc_history = []


        val_acc_history = []




        for it in range(num_iters):




            idx = np.random.choice(N, batch_size)


            X_batch = X[idx]


            y_batch = y[idx]




            # Compute loss and gradients using the current minibatch


            loss, grads = self.loss(X_batch, y=y_batch, reg=reg)


            loss_history.append(loss)




            self.params['W1'] -= learning_rate * grads['W1']


            self.params['b1'] -= learning_rate * grads['b1']


            self.params['W2'] -= learning_rate * grads['W2']


            self.params['b2'] -= learning_rate * grads['b2']




            if verbose and it % 100 == 0:


                print('iteration %d / %d: loss %f' % (it, num_iters, loss))




            # Every epoch, check train and val accuracy and decay learning rate.


            if it % iterations_per_epoch == 0:


                # Check accuracy


                train_acc = (self.predict(X_batch) == y_batch).mean()


                val_acc = (self.predict(X_val) == y_val).mean()


                train_acc_history.append(train_acc)


                val_acc_history.append(val_acc)




                # Decay learning rate


                learning_rate *= learning_rate_decay




        return {


            'loss_history': loss_history,


            'train_acc_history': train_acc_history,


            'val_acc_history': val_acc_history,


        }




    def predict(self, X):


        """


        Use the trained weights of this two-layer network to predict labels for


        data points. For each data point we predict scores for each of the C


        classes, and assign each data point to the class with the highest score.




        Inputs:


        - X: A numpy array of shape (N, D) giving N D-dimensional data points to


          classify.




        Returns:


        - y_pred: A numpy array of shape (N,) giving predicted labels for each of


          the elements of X. For all i, y_pred[i] = c means that X[i] is predicted


          to have class c, where 0 <= c < C.


        """




        W1, b1 = self.params['W1'], self.params['b1']


        W2, b2 = self.params['W2'], self.params['b2']


        s1 = X.dot(W1) + b1


        a1 = np.maximum(s1, 0)


        scores = a1.dot(W2) + b2


        y_pred = np.argmax(scores, axis=1)




        return y_pred

代价函数

to do

y为ground_truth, a为预测。

Regularization

The whole idea of regularization is you try to penalize the complexity of the model, instead of explicitly trying to fit the training data.

creen Shot 2019-03-07 at 4.24.27 P

$L1$ Regularization prefer the sparse weight vector, which

BatchNormalization

zhihu 过程

Dropout

ref1 ref2 ref3 ref4 ref4-ch regularization vs dropout

dropout的引入是为了防止网络的过拟合，本质是正则化。

神经元以概率$p$被保留，当一个神经元被drop out，该神经元的输出就被置0

被drop out的神经元对训练阶段(包括前向传播和后向传播)没有任何贡献，