Dependency structure of sentences shows which words depend on (modify or are arguments of) which other words. These binary asymmetric relations between the words are called dependencies and are depicted as arrows going from the head (or governor, superior, regent) to the dependent (or modifier, inferior, subordinate).
What is Dependency Parsing
Dependency parsing is the task of analyzing the syntactic dependency structure of a given input sentence S. The output of a dependency parser is a dependency tree where the words of the input sentence are connected by typed dependency relations. Formally, the dependency parsing problem asks to create a mapping from the input sentence with words $S = w_0w_1…w_n$ (where $w_0$ is the ROOT) to its dependency tree graph G.
To be precise, there are two subproblems in dependency parsing:
- Learning: Given a training set D of sentences annotated with dependency graphs, induce a parsing model M that can be used to
parse new sentences. - Parsing: Given a parsing model M and a sentence S, derive the
optimal dependency graph D for S according to M.
How to train a Dependency Parsing
Gready Deterministic Transition-Based Parsing
This transition system is a state machine, which consists of states and transitions between those states. The model induces a sequence of transitions from some initial state to one of several terminal states.
States:
For any sentence $S = w_0w_1…w_n$, a state can be described with a triple $c = (\alpha, \beta, A)$:
- a stack $\alpha$ of words $w_i$ from $S$
- a buffer $\beta$ of words $w_i$ from $S$
- a set of dependency arcs $A$ of the form $(w_i,r,w_j)$, where $r$ describes a dependency relation
It follows that for any sentence $S = w_0w_1…w_n$,
- an initial state $c_0$ is of the form $([w_0]_{\alpha},[w_1,…,w_n]_{beta},\empty)$ (only the ROOT is on the stack, all other words are in the buffer and no actions have been chosen yet)
- a terminate state has the form $(\alpha, []_{\beta}, A)$
Transitions:
There are three types of transitions between states:
Shift: Remove the first word in the buffer and push it on top of the stack. (Pre-condition: buffer has to be non-empty.)
LEFT-ARC: Add a dependency arc $(w_j,r,w_i)$ to the arc set $A$, where $w_i$ is the word second to the top of the stack and $w_j$ is the word at the top of the stack. Remove $w_i$ from the stack.
$[w_0, w_1,…,w_i \gets w_j]$
RIGHT-ARC: Add a dependency arc $(w_i,r,w_j)$ to the arc set $A$, where $w_i$ is the word second to the top of the stack and $w_j$ is the word at the top of the stack. Remove $w_j$ from the stack.
$[w_0, w_1,…,w_i \to w_j]$
Neural Dependency Parsing
The network is to predict the transitions between words, i.e., ${Shift, Left-Arc, Right-Arc}$.

For each feature type, we will have a corresponding embedding matrix, mapping from the feature’s one hot encoding, to a d-dimensional
dense vector representation.

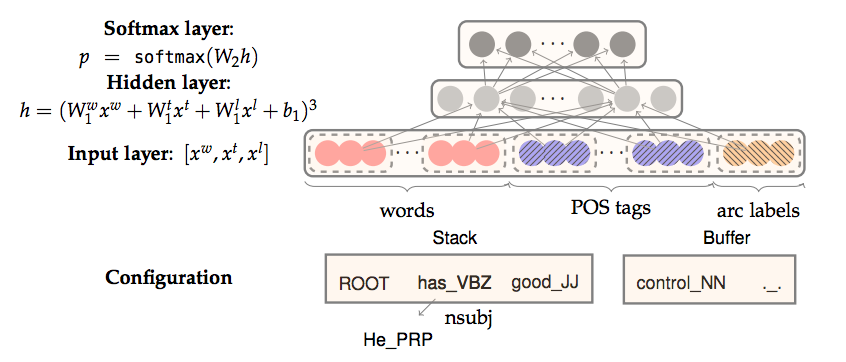
Example
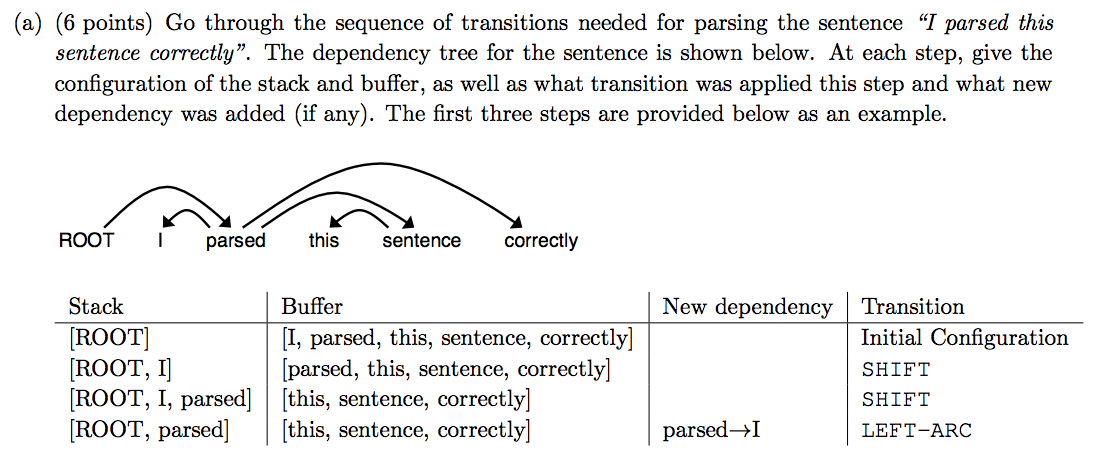
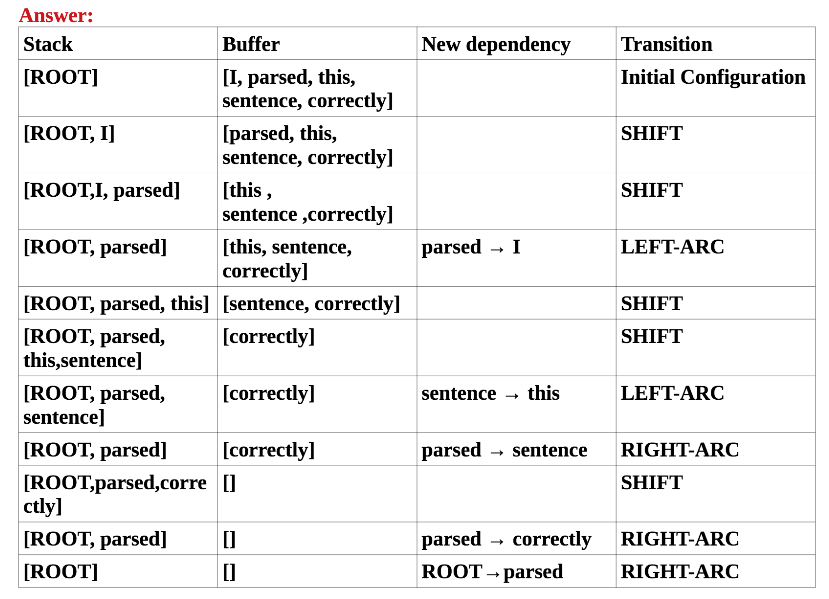
A sentence containing $n$ words will be parsed in $2n$ steps. Because for each word, it will be pushed from buffer to stack, which result in n steps. Then each word in the stack has to be assigned a transition, i.e., LEFT-ARC or RIGHT-ARC, which results in another n steps. Therefore, the total steps are $2n$.
Pytorch Implementation
|
|
Train Parser Network
|
|
|
|