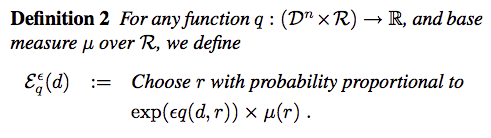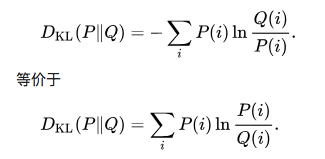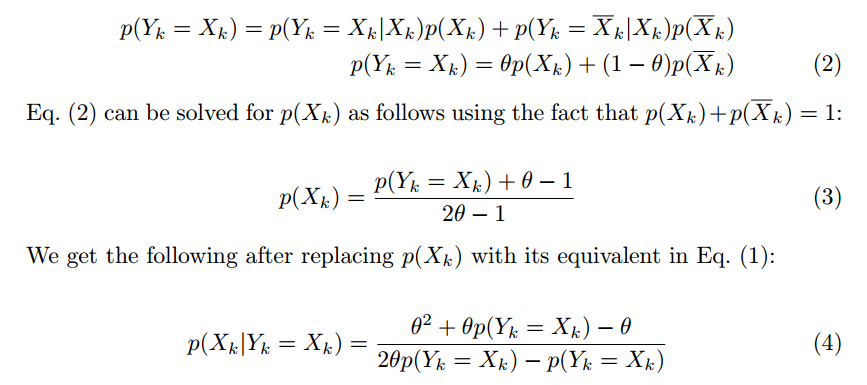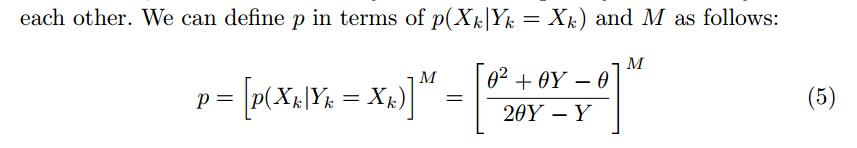Laplace Distribution

The following details are from Wikipedia. And the python version is here

PDF

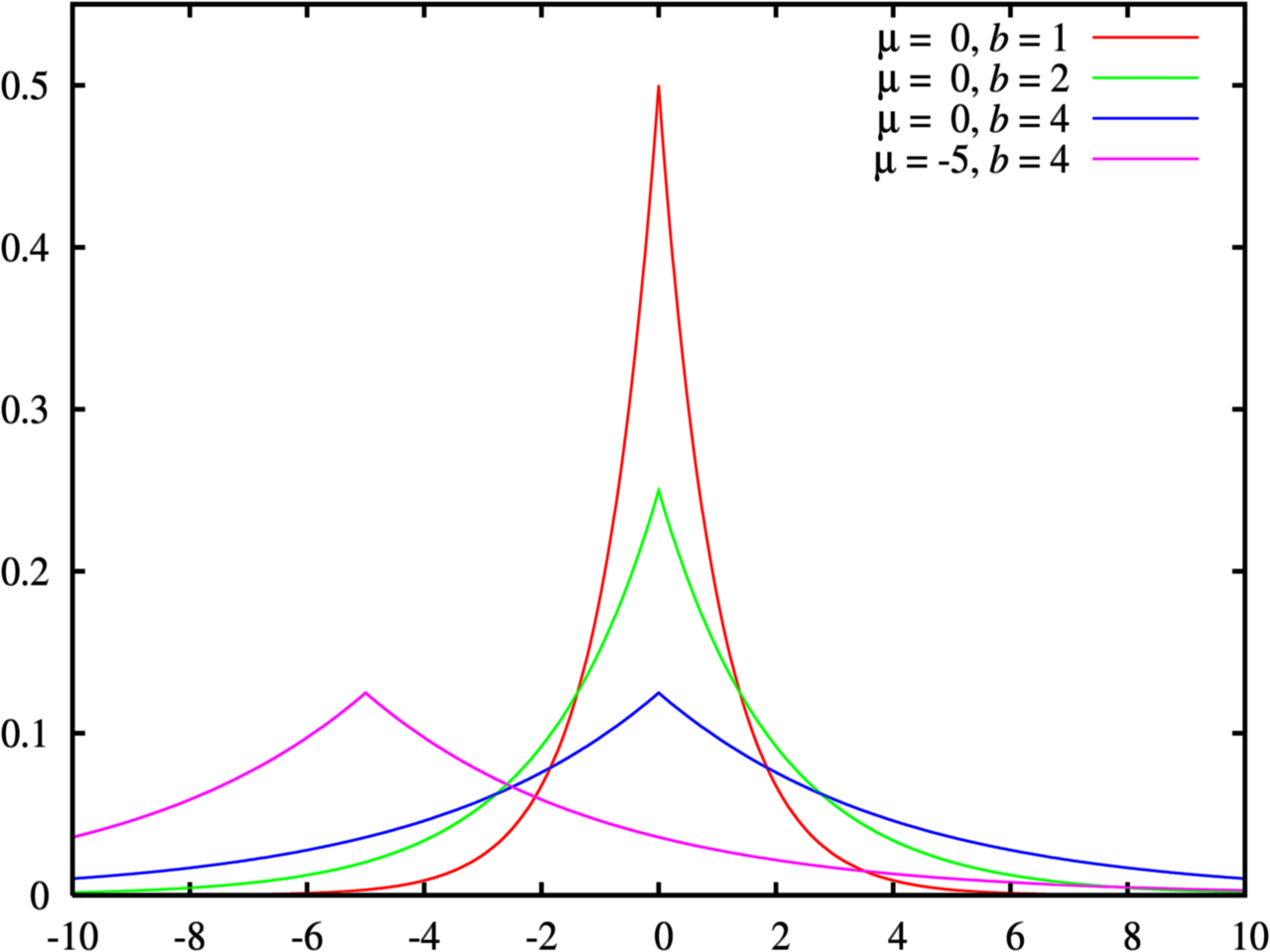
1. 概率密度函数反映了概率在$ x$点处的密集程度。
2. x轴表示每一种取值，而y轴表示概率。
3. the variance of this distribution is $\sigma^2=2b^2$, while its scale is $b$.

CDF

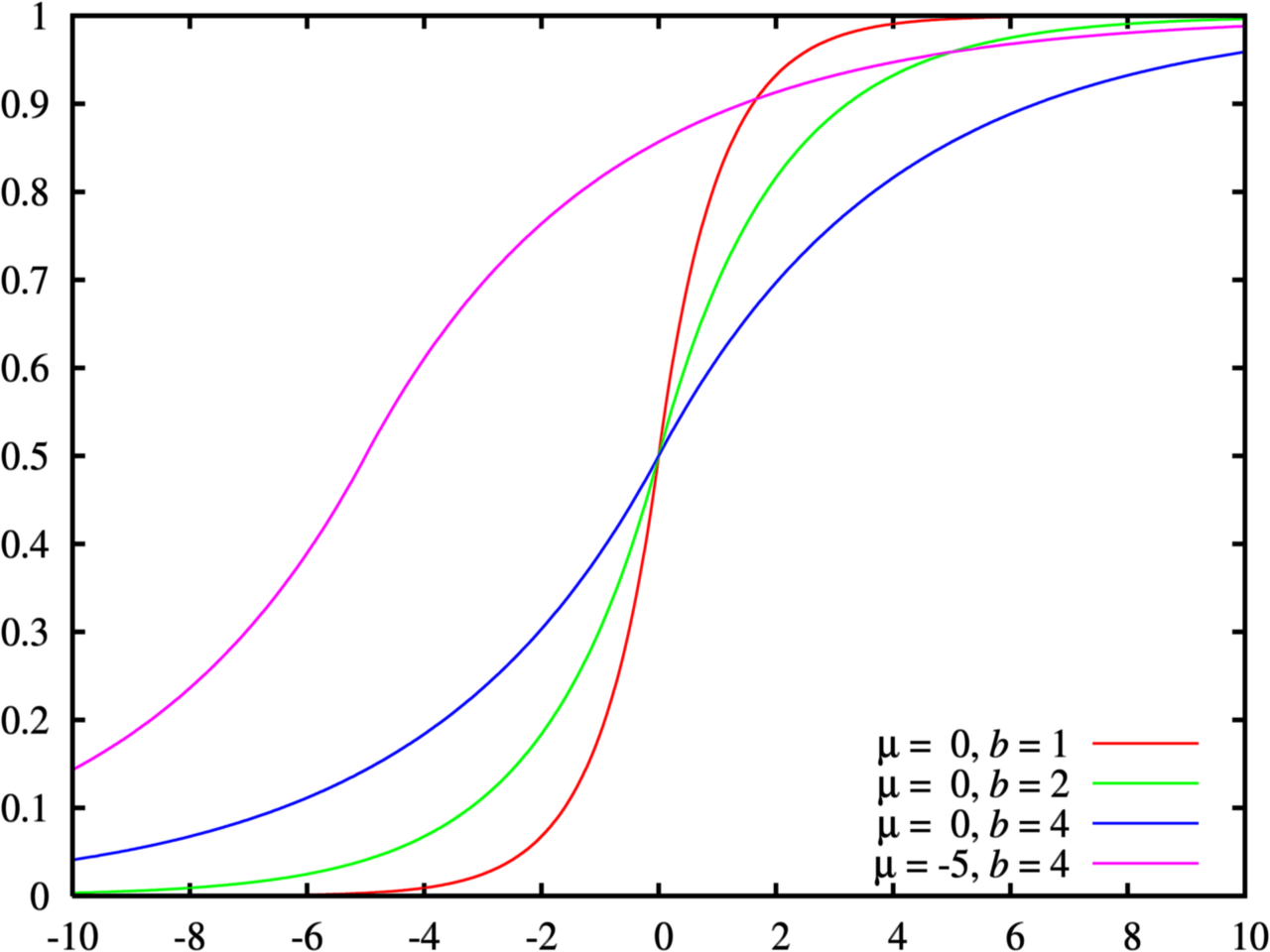
1. CDF表示连续累积概率，即$F(0)=P(x\le{0})$，即所有非正值的概率和。
2. PDF 表示某一点取值的概率$f(0)=P(x=0)=0.5$

Sensitivity

L1-sensitivity

Remarks:

1. $N^{|X|}$ 表示数据库的大小是$|X|$, 即有$X$条记录；而$\mathbb{R}$表示real number，$\mathbb{R}^{k}$则表示$k$维空间，即数据是$k$维的，$k$维向量。

Laplace Mechanism

TO DO QUESTION??

1. WHY LAPLACE DISTRIBUTION????

2. WHY SENSITIVITY IN THE SCALE????

Definition

the Laplace mechanism will simply compute $f$, and perturb each coordinate with noise drawn from the Laplace distribution.

About the proof, the key is that :

1. neighbourhood database:

   $x\in{N^{|X|}}$ and $y\in{N^{|X|}}$, such that $||x-y||_1=\le1$.

2. noise result:

   $\frac{P(f(x)=z)}{P(f(y)=z)}\le{e^{\epsilon}}$

Remarks:

1. Let $\hat{f(x)}$ be the output of Laplace mechanism with zero mean given an input $x$. Then, for ant $x$, $\mathbb{E}[\hat{f(x)}]=f(x)$, where $f(x)$ is true query result without any perturbation.

   $\mathbb{E}[\hat{f(x)}]=\int{P(x)}\hat{f(x)}dx=\int{P(x)(f(x)+n(x))}dx=f(x)\int{P(x)}dx+\int{P(x)n(x)}dx$

   Obviously, $\int{P(x)}dx=1$, since the distribution of $n$ has zero mean so it is symmetric. For any $Pr(x)$, there are always two variables $n_1$ and $n_2$ such that $n_2=-n_1$, resulting in $P(n_1)n_1+P(n_2)n_2=0$. So $\int{P(x)n(x)}dx=0$.

   SO $\mathbb{E}[\hat{f(x)}]=f(x)$

2. The error introduced by $Lap(0,\frac 1 \epsilon) \ is\ \frac 1 \epsilon​$

   Assume $X$ is true answer and $Y=X+n$ is the noise output. $Error^2=E((Y-X)^2)=E(n^2)=E((n-E(n))^2)=E((n-0)^2)=Var(n)$

   so the variance of noise distribution is the error, which is $\sqrt 2 b=\sqrt 2 \frac{1}{\epsilon}$

Properties

Divisibility of Laplace Distribution

Python Implement

1
2
3
4
5

def noise():
    loc = 0
    scale = 1
    noise = np.random.laplace(loc,scale,1) #返回一个list
    return noise[0]

Examples

We sometimes refer to the problem of responding to large numbers of (possibly arbitrary) queries as the query release problem.

1. Counting Queries

   Since the sensitivity of a counting query is 1 (the addition or deletion of a single individual can change a count by at most 1), so $(\epsilon,0)$-differential privacy can be achieved for counting queries by the addition of noise scaled to $\frac{1}{\epsilon}$, that is, by adding noise drawn from Lap($\frac{1}{\epsilon}$). The expected distortion, or error, is $\frac{1}{\epsilon}$, independent of the size of the database.

   A fixed but arbitrary list of m counting queries can be viewed as a vector-valued query. Absent any further information about the set of queries a worst-case bound on the sensitivity of this vector-valued query is m, as a single individual might change every count. In this case $(\epsilon,0)$-differential privacy can be achieved by adding noise scaled to $\frac{m}{\epsilon}$ to the true answer to each query.

2. Histogram Queries

   

Utility

Remarks:

1. Theorem3.8中，Pr[]里面，左边表示Laplace mechanism产生的error，右边中的两项，$t=In(\frac{k}{\delta})$，$k$是query result的维度，$b=\frac{\Delta{f}}{\epsilon}$。
2. 

Exponential mechanism

The exponential mechanism was designed for situations in which we wish to choose the “best” response but adding noise directly to the computed quantity can completely destroy its value, such as setting a price in an auction, where the goal is to maximize revenue, and adding a small amount of positive noise to the optimal price (in order to protect the privacy of a bid) could dramatically reduce the resulting revenue.

Definition

The sensitivity of score function $q$ tells us the maximum change in the scoring function for any pair of datasets $d$ and $d’$ such that $|d\otimes d’|=1$:

Say we have a discrete candidate output in a range $R$, and assume that the probability distribution of output is $u$, commonly uniform. The general mechanism is to design a query function $q:D^n(input)\times{R(output)}\to{\mathbb{R}}$, which assign a real valued score to any pair $(d,r)$ from $D^n\times{R}$. With a prior distribution of candidate output $u$, we amplify the probability associated with each output by a factor of $e^{\epsilon{q(d,r)}}$:

$$\Delta{q}=max_{r\in{R}}\ max_{x,y:||x-y||_1\le{1}}|q(x,r)-q(y-r)|$$

Remarks:

1. by amplifying the probability, the sum of all output probability will not equal 1. So in order to bound the probability, we need a normalization term.

2. from the denifition, if we set the probability factor as $\epsilon$, then it will provide us $2\epsilon \Delta q$, which amptifies with a factor $2\Delta q$. SO if we want $\epsilon$-DP, then the probability factor should be $\frac{\epsilon}{2\Delta q}$

3. the exponential mechanism defines a distribution over the output domain and samples from this distribution.

4. now we want to know how a small change in the database can affect the output. Say we have database $d$ and $d’$, where $||d-d’||=1$. And we assume $q(d,r)=q(d’,r)+\Delta{q}$. we want to bound the probability ratio $\frac{P(r|d)}{P(r|d’)}$

   $$\begin{equation} \begin{aligned} \frac{P(r|d)}{P(r|d')}&=\frac{e^{\epsilon{q(d,r)}}}{\int{e^{\epsilon{q(d,r)}}}}\div\frac{e^{\epsilon{q(d',r)}}}{\int{e^{\epsilon{q(d',r)}}}}\\ &=\frac{e^{\epsilon{q(d,r)}}}{e^{\epsilon{q(d',r)}}}\times\frac{\int{e^{\epsilon{q(d',r)}}}}{\int{e^{\epsilon{q(d,r)}}}}\\ for\ the\ left\ one,\ we\ replace\ q(d,r)=q(d',r)+\Delta{q} ,\\ for\ right\ since\ q(d',r)= q(d',r)-q(d,r)+q(d,r) \\ &={\frac{e^{\epsilon{(q(d',r)+\Delta{q})}}}{e^{\epsilon{q(d',r)}}}}\times\frac{\int{e^{\epsilon{(q(d',r)}-\epsilon{(q(d,r)+\epsilon{(q(d,r)}})}}} {\int{e^{\epsilon{q(d,r)}}}}\\ since\ |q(d',r)-q(d,r)|\le \Delta q,\ so\ we\ have \\ &\le e^{\epsilon \Delta q} \times \int{e^{\epsilon \Delta q}}\\ &=e^{\epsilon \Delta q}\times{e^{\epsilon{\Delta{q}}}}\\ &=e^{2\epsilon \Delta q} \end{aligned} \end{equation}$$

Utility

The exponential mechanism can often give strong utility guarantees, because it discounts outcomes exponentially quickly as their quality score falls off.

Let $OPT_{q}(d)=max_{r\in R}q(d,r)$ denote the maximum score of any candidate output $r\in R$ with respect to database $d$.

Fixing a database $d$, let $R_{OPT}=\{r\in R:q(d,r)=OPT_{q}(x)\}$ denote the set of candidates in $R$ which attain maximum utility score $OPT_q(x)$. Then:

Theorem:

Corollary:

Remarks:

1. We bound the probability that the exponential mechanism returns a “good” output of $R$, where good is measured in terms of $OPT_q(d)$. The result is that it will be highly unlikely that the returned output $r$ has a utility score that is inferior to $OPT_q(x)$ by more than an additive factoc of $O(\frac{\Delta q}{\epsilon}log|R|)$
2. from the utility theorem, we can find that utility of the mechanism only depends on log(|Outputs|), leading to the fact that sampling an output may not be computationally efficient if output space is large.
3. 
4. 

Laplace vs Exponential

Exponential mechanism is an instance of the exponential mechanism.

1. candidate output domain

   Say we have the output domian $r\in R$, and the query function is $f$ which works over the database $d$ and $d’$ such that $|d\otimes{d’}|=1$.

2. utility function

   $$q(d,r)=-|f(d)-r|$$

   To see how this works, notice first that with this scoring function, the exponential mechanism becomes:

   $M(d,q,\epsilon)$=output $r$ with probability proportional to $e^{\epsilon q(d,r)}$

   which provides $2\epsilon \Delta q$-DP.

3. sensitivity

   $$\begin{equation} \begin{aligned} \Delta q &=max|q(d,r)-q(d',r)|\\ &=max||f(d')-r|-|f(d,r)||\\ &\le max|f(d',r)-f(d,r)| \ \ \ \ \ \ \ \ \ \ \ \ \ \ (triangle inequlity)\\ \end{aligned} \end{equation}$$

   So based on above details, for query function with sensitivity 1 and with privacy parameter $\epsilon$, exponential mechanism provides $2\epsilon$-DP, while Laplace mechanism provides $\epsilon$-DP. This is because we’ve used the general analysis of the exponential mechanism, so our result is less “tight”.

   This means that to provide the same privacy level $\epsilon$, laplace mechanism is $\epsilon-$DP while exponential mechanism is $\frac{\epsilon}{2}$-DP, meaning more noise.

Examples

The median mechanism

Recall that the median of a list numbers $d=\{1,2,4,5,6\}$ is 4; so we write $med(d)=4$

1. candidate ooutputs

   every element in $d$ is the possilble output of the median query.

2. utility function

   For the median example, our scoring function will be:

   $q(d,r)=-min|d\otimes d’|$ such that $med(d’)=r$

   What does it mean? The idea is that we take in a database $d$ and a candidate median $r$, and we look for a $d’$ that is as similar as possible to $d$, such that $med(d’)=r$.

   For example, $d=\{1,2,3,4,5\}$ and candidate output $r=4$. What we want to do is to change $d$ to $d’$ so that $med(d’)=4$. To do so, we can remove $1$ and $2$ from the $d$ to get $d’=\{3,4,5\}$. so $q(\{1,2,3,4,5\},4)=-2$. If $r=3$, $q(\{1,2,3,4,5\},4)=0$ becasue $3$ is the true median and we needn’t change anything about database $d$.

3. sensitivity

   We can get $|q(d,r)-q(d’,r)|\le 1$. It is obvious because the input database is added or removed one element, for the unchanged database, the change you make to make $r$ median is $x$ step. Now we have already help you make a step. So the best situation is you only need to maek (x-1) step for x as median. The utility change is 1. While the worst situation is the addition or removal in the original database don’t help you at all, so you still need $x$ step. So the utility change is 0.

   There is the mathametical proof.

   

   

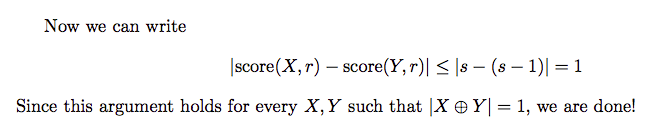
Composition Theorems

[2009-McSherry] Any approach to privacy must address issues of composition: that several outputs may be taken together, and should still provide privacy guarantees even when subjected to joint analysis

[2014-Dwork] The combination of two differentially private algorithms is differentially private itself. But the parameters $\epsilon$ and $\delta$ will necessarily degrade —- consider repeatedly computing the same statistic using the Laplace mechanism. The average of the answer given by each instance of the mechanism will eventually converge to the true value of the statistic, and so we cannot avoid that the strength of our privacy guarantee will degrade with repeated use.

Sequential composition

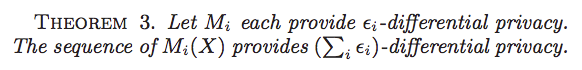
Proof:

$$\begin{equation} \begin{aligned} Pr(M(X)=O)& =\prod_{i=1}^{m}Pr(M_i(X)=O_i) \\ &\le \prod_{i=1}^{m} e^{\epsilon_i}Pr(M_i{(X')=O_i})\\ &=e^{\sum_{i=1}^{m}\epsilon_i}\prod_{i=1}^{m} Pr(M_i(X')=O_i)\\ &=e^{\sum_{i=1}^{m}\epsilon_i} Pr(M_i(X)=O) \end{aligned} \end{equation}$$

x

Parallel composition

While general sequences of queries accumulate privacy costs additively, when the queries are applied to disjoint subsets of the data we can improve the bound. Specifically, if the domain of input records is partitioned into disjoint sets, independent of the actual data, and the restrictions of the input data to each part are subjected to differentially-private analysis, the ultimate privacy guarantee depends only on the worst of the guarantees of each analysis, not the sum.

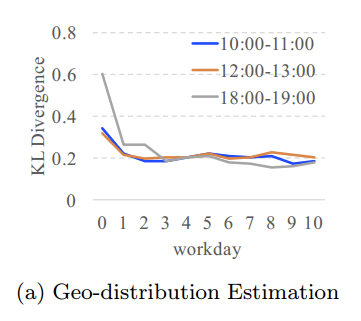
KL-Divergence

又叫相对熵，是衡量分布间距离的一个度量。

定义

设$P(i)​$和$Q(i)​$是$X​$取值的两个概率分布，则$P​$相对$Q​$的KL-Divergence是：

性质

1. 非对称性

   $$D(p||q)\ne{D(q||p)}$$

2. 非负性

   $$D(p||q)\ge0$$

[2011-Aaron]

Reference

[2014-Dwork] The Algorithmic Foundations of Differential Privacy

[2006-Dwork] Calibrating Noise to Sensitivity in Private Data Analysis

[2009-McSherry] Privacy Integrated Queries

[2016-Gunther Eibl] Differential privacy for real smart metering data

This post is about my learning process of probability and statistics.

[2016-Atsushi] gives a comprehensive survey about random response. Randomized response tends to be used in data collection scenario.Randomized response is purely a client-based privacy solution. It does not rely upon a trusted third-party server and puts control over data back to clients. The basic idea is answer truthfully with probability $p$, and answer randomly by picking a answer from the rest choices with probability $1-p$. And the rest choices include the true answer.

Random Response and its Variant

Definition[2016-Wang]

Warner Version

Random response was first proposed by [1965-Warner]. The aim is to estimate the proportion $\pi(A)$ of people who have some attribute A.

Each user has reports her true answer $t\in \{1,-1\}​$ with probability p, and a random answer with probability 1 − p. The latter has the same probability to be −1 and +1;

Framework

1. There are red cards and non-red cards in a box, where the ratio of red cards among all the cards is $q$ with $0 < q < 1$ and $q \ne \frac{1}{2}$. And user draws a card.
2. If red, answer truthfully to the question “I am a member of A”
3. Otherwise, answer truthfully to the question “I am a member of A”

Utility

Let $\hat{T}$ be the proportion to which the respondents reply “True.” It is easy to see that the expectation of $\hat{T}$ is:

Privacy Analysis

According to the definition of Differential Privacy, the following ratio should be bounded,

$P(A|A)=q​$

$P(A| not \ A)=(1-q)$

So combining the above two, we have:

The randomized response satisfied $\epsilon$-Differential Privacy, where

Kuk Version

Kuk’s proposed another kind of randomized response mechanism to estimate the proportion $\pi_A$, the same as Warner’s mechanism.

Framework

1. There are two boxes, $BOX_1$ and $BOX_2$. There are red and non-red cards in each box and the ratio of red cards in each box is $q_1,q_2$ respectively, where $0<q_1,q_2<1, q_1\ne{q_2}$. User takes one card from each box.
2. If this user is a member of A, then replies “red card” or “non-red card” in accordance
   with the card taken from $BOX_1$
3. Otherwise, he does the same as above except that he takes a card from $BOX_2$.

Privacy Analysis

Negative Survey Mechanism

Framework

Privacy Analysis

t-times Negative Survey

Privacy Analysis

Application

[2011-Quercia]

Framework

[2011-Quercia] uses random response to obfuscate locations.

Let $k$ be the number of locations on a map. Then, the main part of SpotMe works as follows:

1. the mobile phone chooses the location k uniformly at random with probability $p$
2. it chooses the true location with probability $1-p$

Privacy Analysis

According to the definition of Differential Privacy, the following ratio should be bounded,

$$P(L_{noise}|L_{true})\le{e^{\epsilon}P(L_{true}|L^{'}_{true})}$$

where $L_{true}$ is user’s actual location and $L^{‘}_{true}$ is the user’s location after making some changes while $L_{noise}$ is user’s obfuscated location.

$P(L_{true}|L_{true})=(1-p)+p*\frac{1}{k}$

$P(L_{true}|L^{‘}_{true})=p*\frac{1}{k}$

so after combining above two formulations, we have privacy bugdet:

$$\epsilon=ln\frac{k-(k-1)p}{p}$$

[2016-Wang]

Randomized Response vs. Laplace Mechanism

Randomized Response

Without loss of generality, we assume the randomized response still favors the true value, i.e., $p_{00}, p_{11} > 0.5$. Intuitively, under the same privacy standard, the mechanism with larger diagonal elements in the corresponding design matrix tends to achieve better utility.

• 
• What is the proportion of $X=1$? It aims to o learn the population distribution based on the collected randomized dataset. We use $\pi_1$to denote the true proportion of value 1 to be estimated in the original population. The observed proportion of value 1 in the collected dataset is denoted as $\lambda_1$. We denote the unbiased estimator for $\pi_1$ respectively as $\hat{\pi}_1$.

• 

  Laplace Mechanism

• 

• 
• 

[2006-Huseyin]

One-Group Schemes vs Multi-Group Schemes.

in my understanding, one-group means there arw n users and m items. for a user, all the items rating are in a group. For example, user_i’s true rateing for all items is (0101),with probability theta to upload (0101) and (1-theta) probability to upload (1010).

And in m-group, for example m=2, then user_i’s rating is (01)and(11). with probability theta1 to upload (01) and (1-theta1) to upload (10); theta2 to upload(11) and (1-theta2) to upload (00)

Although we achieve decent accuracy in this scheme, the privacy level is very low. We improve privacy level by introducing multi-group schemes, while with increasing M, accuracy decreases because we add more randomness. The accuracy is from how much info is preserved after randomness. The more info, the more accurate. P(true=x|randon resp = x) means preserved info. m-group info preserved: $P^m$

Private Mechanism With Full Privacy

[2014-Sun]

The problem setting is how to find frequent itemset with privacy. Say we have the item set $I={I_1,I_2,..,I_n}$. Before each user sends out their transaction which is $n$-dimention vector and ithe entry being 1 means this user has this item or else, he does the the randomized selection for each item. That is, keep true answer with probability $p_i$ for item i and perturb the answer with $1-p$. And p controls the privacy level.

For k-itemset, we want to find out its support, which comes from the estimator based on the perturbed data. Say we want to calculate the support of $2$-itemset. And the item set is $\{A,B,C,D\}$. And the candidate domain is $\{AB,AC,AD,BC,BD,CD\}$. The aim is to get the true count of $AB, \ c(AB)$, which is $11$ and may comes from $\{00,01,10,11\}$, with the probability matrix $P=\matrix{p_{00},p_{01}\\p_{10},p_{11}}$. so based on the observed count of $[A=0,B=0],[A=0,B=1],[A=1,B=0],[A=1,B=1]$ we can get estimator count matrix by $C_{observed}=PC_{estimator}\to C_{estimator}=P^{-1}C_{observed}$. And the support for $AB$ is $C_{estimator}[-1]$.

Basic RAPPOR

[Building a RAPPOR with the Unknown: Privacy-Preserving Learning of Associations and Data Dictionaries]

Reference

[2011-Quercia] SpotME if you can: randomized responses for location obfuscation on mobile phones

[1965-Warner] Randomized response: a survey technique for eliminating evasive answer bias

[2016-Wang] Using Randomized Response for Differential Privacy Preserving Data Collection

[2006-Huseyin] Achieving Private Recommendations Using Randomized Response Techniques

[2014-Sun] Personalized Privacy-Preserving Frequent Itemset Mining Using Randomized Response

[]

Q?

1. WHY $r$?

   The author investegate the $l$-privacy within $r$.

2. [2013-Andres] paper don’t understand “polar mechanism is discretized and truncated?”

Problem Setting

The goal of location with DP is that the chance of users being mapped to one specific obfuscated location from any of the actual locations is similar. The more similar the probability for each region is, the harder it is to infer users’ original positions, leading to better privacy protection.

[2014-To] details the methods of Private Spatial Decompositions.

Reference

[2014-To] A Framework for Protecting Worker Location Privacy in Spatial Crowdsourcing

[2015-Layla] is a survey on the MobileCrowdScoucing privacy.

Four factors in CrowdSourcing:

1. sensing data quality, which tries to maximize the data quality measured by a certain metric (mostly used in environmental monitoring tasks)
2. incentive cost, which aims at minimizing the total budget (from the task organizer perspective)
   for an MCS task with different incentive mechanisms, such as pay per participant or pay per task
3. energy consumption, whose objective is to identify an optimal collaborative data sensing and uploading scheme with energy-saving techniques such as piggybacking
4. travel distance, where the travel distance of a user for accomplishing a task is considered in task allocation, in order to minimize the overall travel distance for all the tasks.

[2018-Wang Jiangtao] provides the comprehensive survey on MCS(MobileCrowdScoucing) task allocation.

Task Assignments in CrowdSourcing

In croudsourcing, workers with mobile devices to collect data and send it to task requester for rewards.

In task assignment, organizers need participants’ precise locations for optimal task allocation. However, the exposure of their locations raises privacy concerns. Especially for those who are not eventually selected for any task, their location privacy is sacrificed in vain.

So in the differential privacy task assignment croudsourcing, the goal is to design a data release method that accurately represents the distribution of the workers and helps the Server efficiently match workers with tasks without compromising the privacy of their locations.

Solutions

[2014-To]

it is the first one to solve this problem.

1. Framework

   • Workers send their locations to a trusted cellular service provider(CSP)
   • CSP collects updates and releases a PSD according to privacy budget 
   • When the SC-server receives a task t, it queries the PSD to determine a geocast region (GR), which is a unique feature of this work. Next, the SC-server initiates a geocast communication process to disseminate t to all workers within GR. Upon receiving request t, a worker w decides whether to perform the task or not.
   • Task assignment.
     • Once server get a task request, server needs to query PSD to find a geocast region, balancing between high task assignment success rate and system overload like worker traveling distance and the number of noticed worker. The author calculate maximum travel distance, models acceptance rate as the function of distance.
     • Geocast region construction.
     • Optimization. Including Partial Cell Selection and Communication Cost.

2. Privacy Model

   • Privacy leakage: (1) workers disclose information to the task requester once they consent to the task; (2) completion of a task discloses the fact that some worker must have been at that location; (3) but this paper focuses on what happens prior to consent, when worker location and identity must be protected from both task requesters and the SC server.

   • the specific objective is to protect both the location and the identity of workers during task assignment.

   • Private Spatial Decom

     • AG uses a two-level grid and variable cell granularity.

     • For the first-level, domain is divided into $m_1\times{m1}$ cells. This heuristic method is data-independent, and thus does not consume any privacy budget. For each level-1 cell, it is divided into $m_2\times{m2}$ subcells.

       $$m1 = max(10,\lceil{\frac{1}{4}\sqrt{\frac{N\times{\epsilon}}{k_1=10}}}\rceil) \\ m_2=\lceil{\sqrt{\frac{N'\times{\epsilon_2}}{k_2=5}}}\rceil$$

     • $k_2$ selection. $k_2$ controls the granularity of level-2 domain and small one leads to compactness in level-2 subcells.

     • improving $m_2$

       

[2018-Yang]

it criticizes that [2014-To] is based on the assumption that workers are uniformly distributed within the domain and and the workers in each cell have the same acceptance rate. So they proposes a workers density-based method.

1. Framework
   • Workers must submit their location to the CSP, travel to the location designated for the task and collect data using their sensor-equipped device.
   • The CSP collects locations from workers and releases data in sanitized form to the Server for task assignment. There is a trust relationship between CSP and workers.
   • The Server queries the CSP for a sanitized dataset once it receives a task, where server chooses a geocast region GR to disseminate the task to the workers in GR. It then assigns the task to suitable workers, through the CSP, according to a task assignment algorithm.
2. Modules
   • Using quadtree to partition the region based on worker density. But the authors change this method so that the partitioning is based on the worker density instead of choosing the middle point.
   • Partitioning point selection. Before partitioning, m initial points are randomly generated within the cell, ==============================(TODO)
   • Differential privacy data release. A noisy count of the number of workers in each cell is released to protect the privacy of worker locations, where whether or not a worker
     within a specific cell cannot be identified.
   • Task assignment. Firstly, teh geocast region is selected based on task assignment success rate and system overhead (the distance workers need to travel and the number of workers notified of the task).
3. Privacy Model
   • The basic idea of private data release is that the domain of worker locations is partitioned into small cells and Laplace noise is added to the count of workers in each cell to achieve a differential privacy guarantee.
   • Pervious literature assumes the worker locations are distributed uniformly, and the workers in each cell have the same acceptance rate, which is not the case in real-world scenarios. Partitioning the data domain into a uniform grid would result in sizeable errors. Therefore, we propose a recursive partitioning process based on worker density.
   • The aim is to identify dense regions and sparse regions and make the distribution of the workers in each smaller region as near to uniform as possible.
   • Adopting data-independent quadtree into workers density-based data-independent technique.
     • Partitioning stop condition. Traditional quadtrees require the data publisher to specify the height of the partitioning. In this paper, the process stops if (1) no workers exist in the cell; (2) the area of cell is less than some threshold, The smaller the cell, the more uniform the distribution of workers within it; (3) the distribution of workers in a cell is relatively uniform， which is measures by the threshold of maximum density difference.
     • First, $m$ initial partition points in the location domain need to be selected, where $m=\frac{\sqrt{area \ of \ cell}}{\alpha}$
     • check condition (1) and (2), which is the number of points in cell is greater than 0 and the area of cell is greater than the threshold. If one of answers is no, stop partitioning.
     • for each partitioning point, calculate the density of the subcells divided by this point. choose the point which has the maximum density difference bbetween subcells.
     • If the biggest density difference is greater than the threshold β, the cell is partitioned at point. Otherwise, the cell will not be partitioned as the distribution of worker in the cell is already close to uniform. For example, the density of four subcells is 1, 2, 1, 2, which means in each subcells, there are 1, 2, 1 and 2 points in each subcell, which is kind of uniform distribution in the cell.

[2017-Wang]

1. Framework

   • Platform-side : Geo-Obfuscation Function Generation
   • User-side : Location Obfuscation
   • Platform-side : Obfuscation-aware Task Allocation

2. Privacy Model

   Overall, the aurhor models workers’ travel distance to task locations as the function of geo-obfuscation function and task allocation. And by calculating the optimal function, we can get the Geo-Obfuscation matrix which satisfies DP and task allocation schemes.

   

   • the expected travel distance of assigning a task at $l_t$ to a user at (obfuscated) $l*$ given the geo-obfuscation function $P$.

     

   • optimal function

     

     

     

   • task allocation

     

   • Candidate Geo-Distribution Estimation

     

   • Laplace

     

   • Geo-distribution Estimation

     

     

     

[2015-Gong]

[2016-Jin]

This paper considers how to effectively incentivize worker participation. And proposes a system framework that integrates an incentive, a weighted data aggregation, and a data perturbation mechanism which protects the sensing data.

1. Framework

   

   • Aggregation Mechanism

     To guarantee that the perturbed results have satisfactory accuracy, the original aggregated results before perturbation need to be accurate enough in the first place. Therefore, we reasonably assume that the platform uses a weighted aggregation method to calculate the aggregated result $x_j$ for each task $\tau_j$ based on workers’ data.

     The motivation for utilizing weighted aggregation is to capture the effect of workers’ diverse skill levels on the calculation of the aggregated results.

   • Incentive Mechanism

     aim to design a pSRC auction that minimizes the platform’s total payment with satisfactory data aggregation

     

     where $y_i$ means worker is seleted for a task, $\alpha_j$ is the error threshold for task j, $\theta_{i,j}$ is error of worker i for task j.

2. Privacy model

   • workers locally sense a specific object or phenomenon and server aggregrate the uploaded data and publish a noise aggregated results to protect worker’s privacy.

   • the noise scale is deviated from the $(\alpha,\beta)-accuracy$.

   • 

   • 

   • 

     Remarks:

     $Pr(|N_j|\ge\alpha_j)=Pr(N_j\ge\alpha_j)+Pr(-N_j\le-\alpha_j)$

     according to the symmetry of PDF, $Pr(N_j\ge\alpha_j)=Pr(-N_j\le-\alpha_j)$

     so $Pr(|N_j|\ge\alpha_j)=2Pr(N_j\ge\alpha_j)$

Data Sensing in CrowdSourcing

Solutions

[2016-Wang]

In this paper, instead of studying task assignment, the author focuses on sparse croudsensing. Due to large target sensing area and limited budget which result in insufficient spatial coverage of mobile users, sparse mobile croudsensing impute information of the uncovered regions by combining historical records with available sensing data from nearby regions.

1. Framework
   • The server side generates probabilistic obfuscation matrix and data adjustment function in an offline way.
   • user sider senses its actual location and then maps the associated region to another region according to probabilistic obfuscation matrix. After that, the data adjustment function alters the original sensing data to fit the properties of the obfuscated region. Finally, mobile client then uploads the modified region and data to the server.
   • The server side does data inference : modeled as a matrix completion problem, where each element in the matrix is the value like temperature of a region at time t. In this paper, they use compressive sensing theory for inference.

2. Privacy Model

   • Privacy leakage : In Sparse MCS, participants report the sensing data with time stamps and geographical coordinates, which may introduce serious privacy risks.

   • Data utility: Due to location obfuscation, the uploaded region data is not actual value of this region, so adjustment is needed to decrease data utility loss. the data quality loss is determined by the difference of sensing data between the actual and the obfuscated locations, instead of the geographic distance. In other words, a participant’s location may be mapped to a place far away, as long as the sensing values of the two locations are close enough.

   • Adversary model - Bayesian attack

     

     

     

   • optimal function

     The authors model the sensing data quality loss as the function of location obfuscation matrix.

     

     

     

Reference

[2014-To] A Framework for Protecting Worker Location Privacy in Spatial Crowdsourcing

[2018-Yang] Density-Based Location Preservation for Mobile Crowdsensing With Differential Privacy

[2016-Wang] Differential Location Privacy for Sparse Mobile Crowdsensing

[2015-Layla] Participant privacy in mobile crowd sensing task management: A survey of methods and challenges

[2015-Gong] Protecting Location Privacy for Task Allocation in Ad Hoc Mobile Cloud Computing

[2016-Jin] INCEPTION: Incentivizing Privacy-Preserving Data Aggregation for Mobile Crowd Sensing Systems

[2018-Wang Jiangtao] Task Allocation in Mobile Crowd Sensing: State of the Art and Future Opportunities

动态规划

这篇文章详细记录LeetCode上各种难度的动态规划题目。每道题我都给出题目，思路以及Python代码。

This post is about the definition of Differential Privacy. DP ensures privacy by randomness. So before the definition of DP, we need to know what is randomized algorithms.

In this post, Domain is represented as $\mathbb{N}^{|X|}$, where $|X|$ means the element number of the domain; Range is represented as $\mathbb{R}^{|k|}$, where $k$ means the element is $k$ dimentions.

Range(A) means the output of the mechanism A.

从零开始学贪心算法

贪心算法是指在对问题求解时，总是做出在当前看来是最好的选择。也就是说，不从整体最优上加以考虑，只做出在某种意义上的局部最优解。贪心算法不是对所有问题都能得到整体最优解，关键是贪心策略的选择，选择的贪心策略必须具备无后效性，即某个状态以前的过程不会影响以后的状态，只与当前状态有关。

Hexo Basic Commands

create a blog

hexo n “name of blog”

post a blog