There’s a whole class of NLP tasks that rely on sequential output, or outputs that are sequences of potentially varying length. For example,
- Translation: taking a sentence in one language as input and outputting the same sentence in another language.
- Conversation: taking a statement or question as input and responding to it.
- Summarization: taking a large body of text as input and outputting a summary of it.
Therefore, in this post, sequence-to-sequence models are introduced, a deep learning-based framework for handling these types of problems.
The Seq2Seq Model
The sequence-to-sequence model is an example of a Conditional Language Model.
- Language Model because the decoder is predicting the next word of the target sentence y
- Conditional because its predictions are also conditioned on the source sentence x
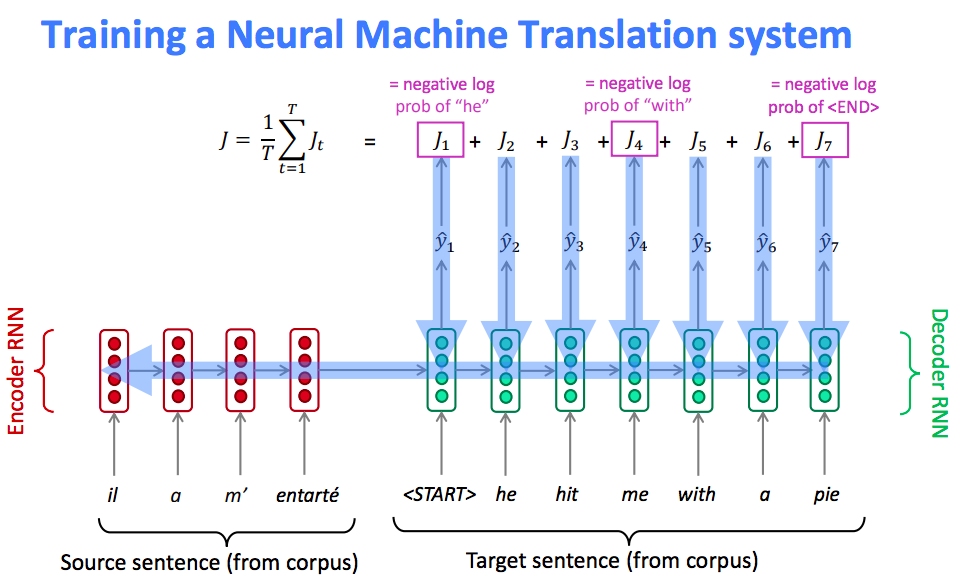
NMT directly calculates $P(y | x)$,
Here $P\left(y_{T} | y_{1}, \ldots, y_{T-1}, x\right)$ is the probability of next target word given target words so far and source sentence $x$.
Output decoding
Greedy decoding
When generating next word, we always take the most probable word on next step and we stop untl the model produces a <END> token.
But this method has no way to undo decisions.

Beam search decoding
Core idea
On each step of decoder, keep track of the k most probable partial translations (which we call hypotheses). Here k is the beam size.
A hypothesis has a score which is its log probability:
- Scores are all negative, and higher score is better
- We search for high-scoring hypotheses, tracking top k on each step
Stop criterion

Selection criterion
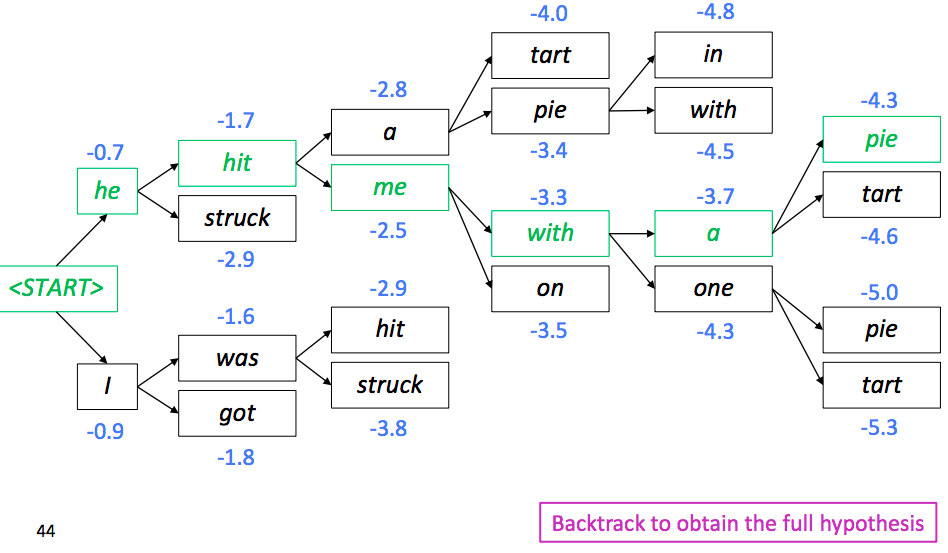
We have our list of completed hypotheses, but How to select top one with highest score?
Say if we choose the hypothese with highest score, which is computed by:
Then it will tend to choose the shorter sentence, which usually has a higher score.
In this case, we fix it by normalizing by length:
and use this to select top one.
Example
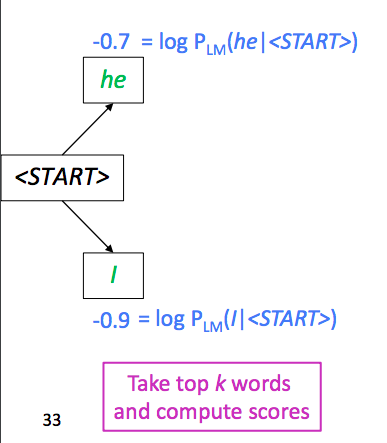
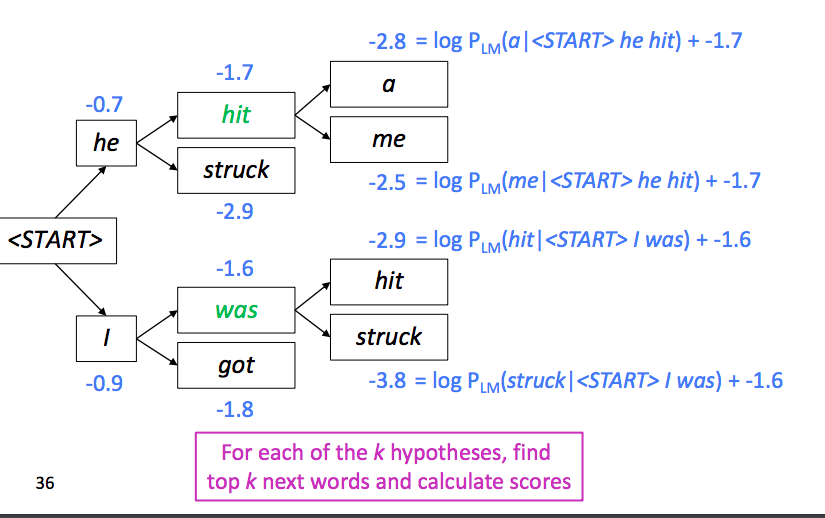
Say we set k=2. We start generation with <START> token. Suppose the top two candidates are he and I:
Then we keep track of the two lines to generate next words:
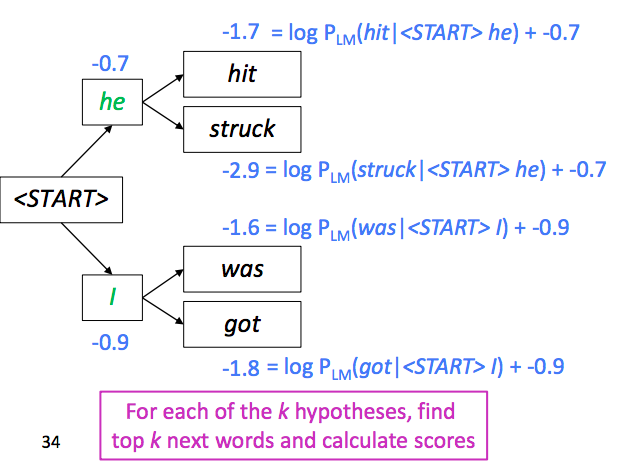
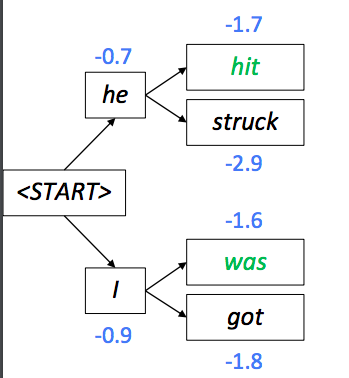
The new score is parent’s score plus current probablity. Here we have four candidates, but since our k is 2, we choose top 2 among these 4 candidates.
Machine Translation Evaluation
BLEU (Bilingual Evaluation Understudy) is the one we use for evaluation. BLEU compares the machine-written translation to one or several human-written translation(s), and computes a similarity score based on:
- n-gram precision (usually for 1, 2, 3 and 4-grams)
- Plus a penalty for too-short system translations
BLEU is useful but imperfect:
- There are many valid ways to translate a sentence
- So a good translation can get a poor BLEU score because it
has low n-gram overlap with the human translation
The Attention Mechanism
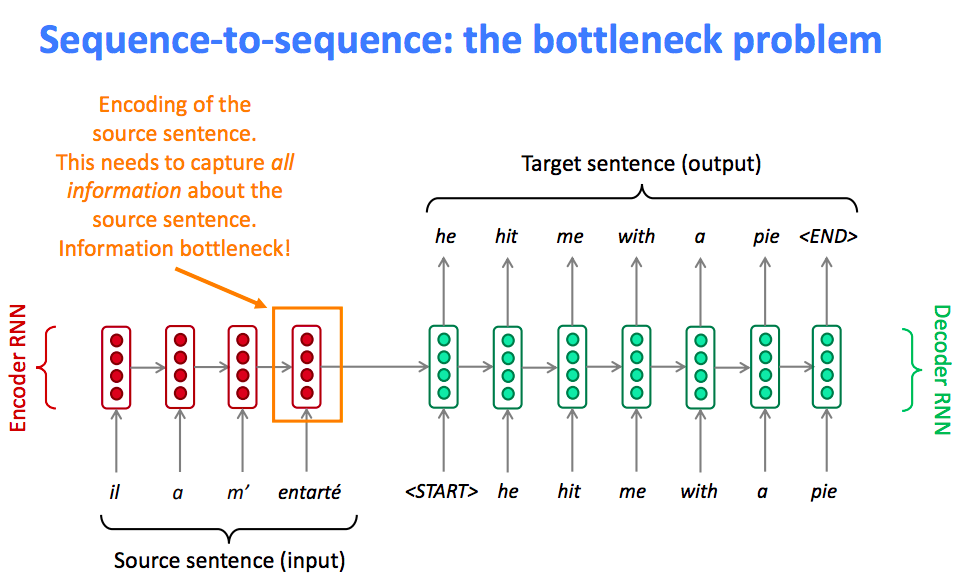
Problem in Seq2Seq
The fixed-length vector carries the burden of encoding the the entire “meaning” of the input sequence, no matter how long that may be. With all the variance in language, this is a very hard problem.
Core ideas
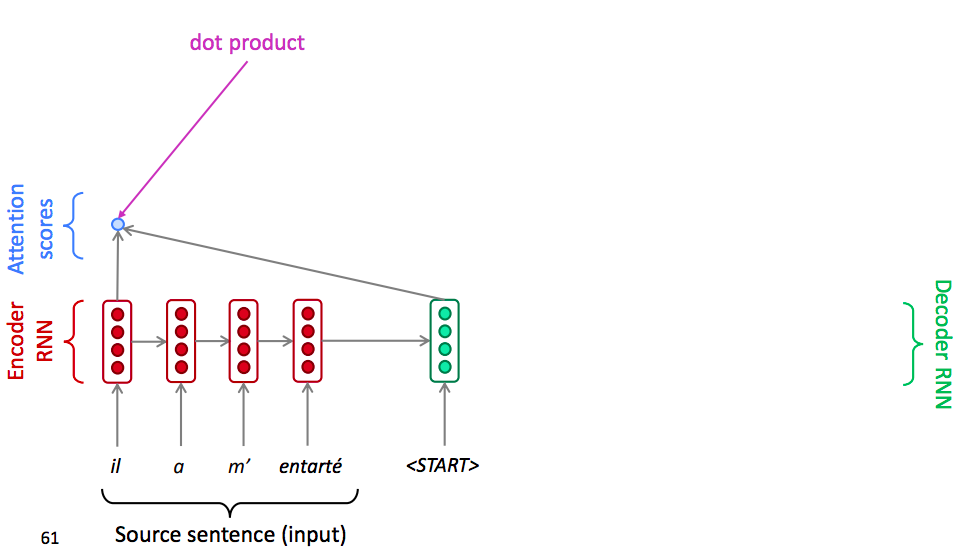
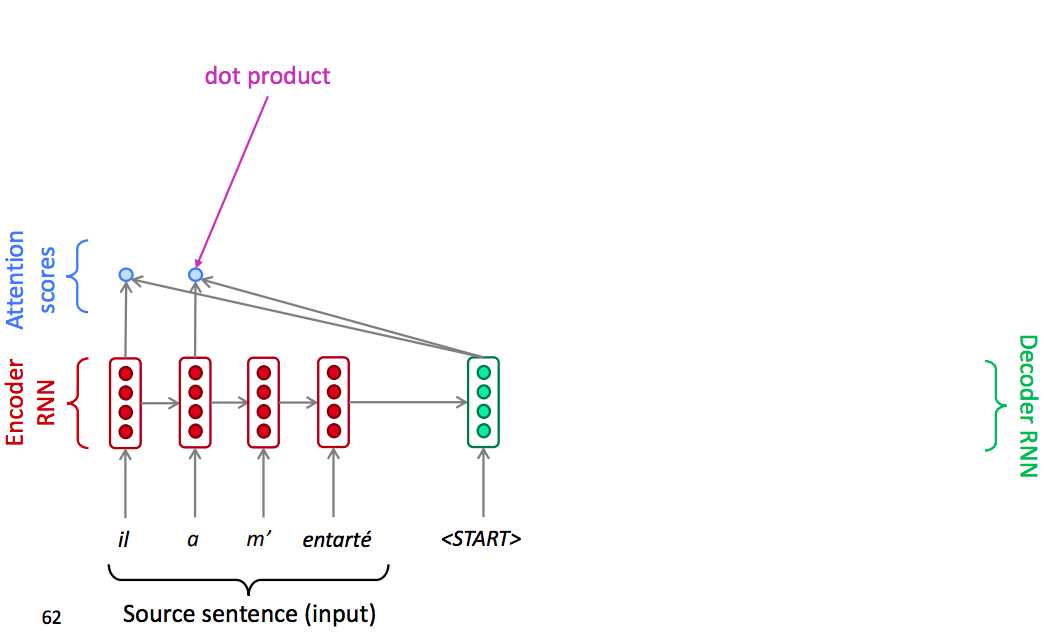
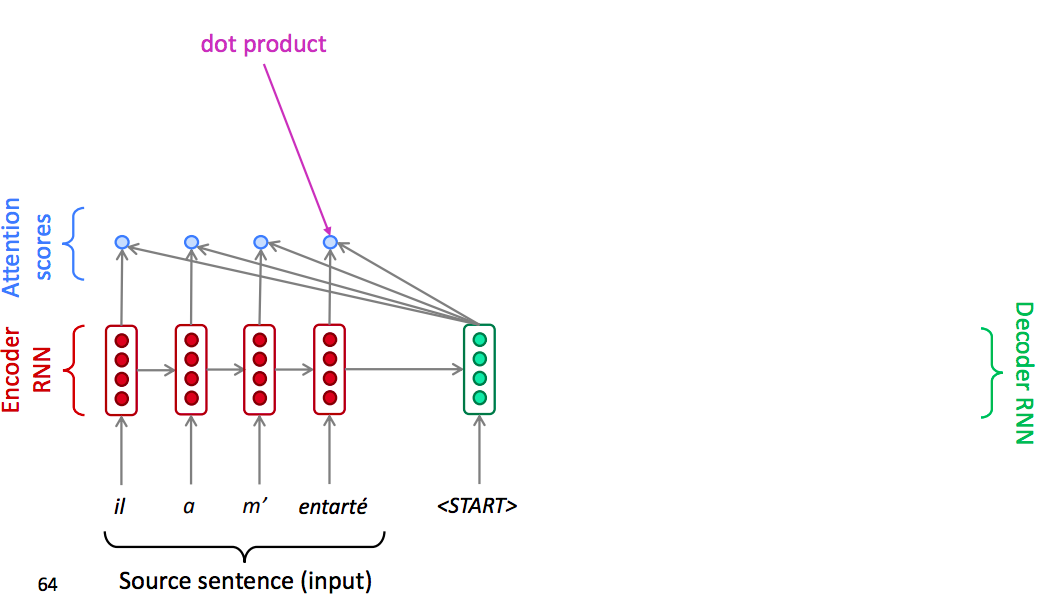
In decoder, insted of just use the hidden state at the first step of the decoder, we operate the dot product between the decoder hidden state with the encoder hidden state of each step in encoder. So that we can get several scalar scores.
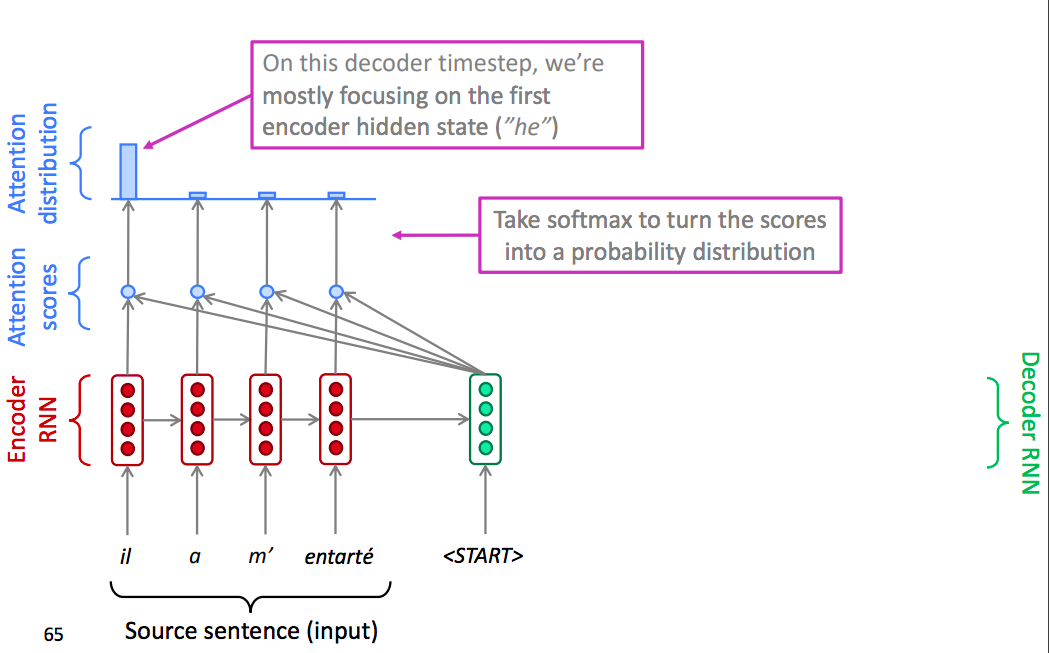
Once we have these scores, we use a softmax function to turn the scores into a distribution.
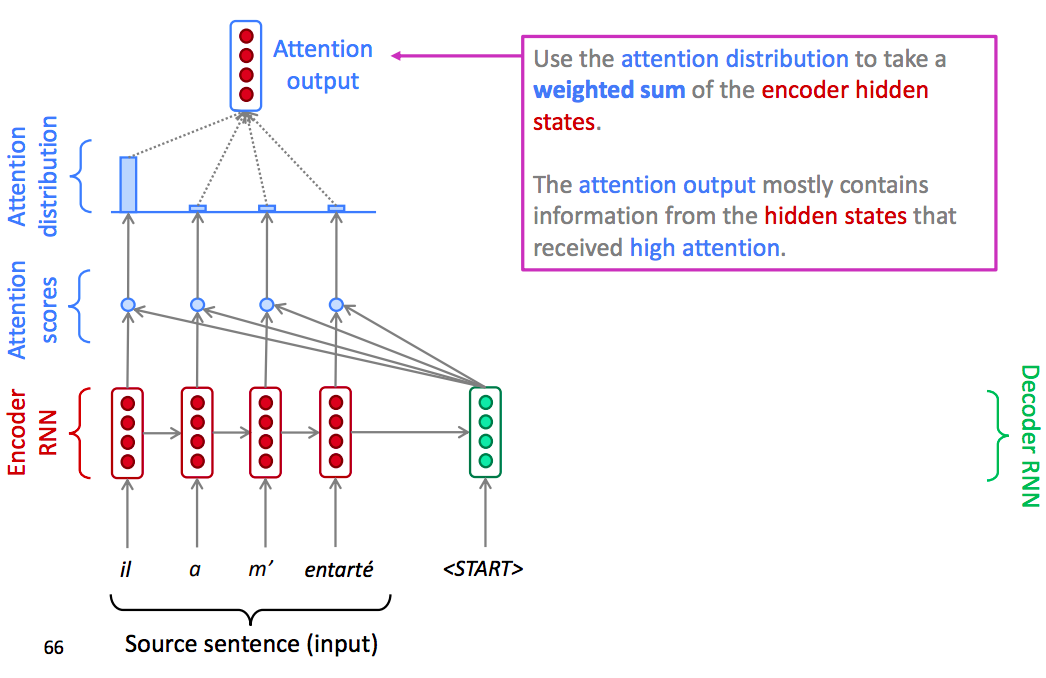
Once we have the attention output, we use the attention distribution to take a weighted sum of the encoder hidden states.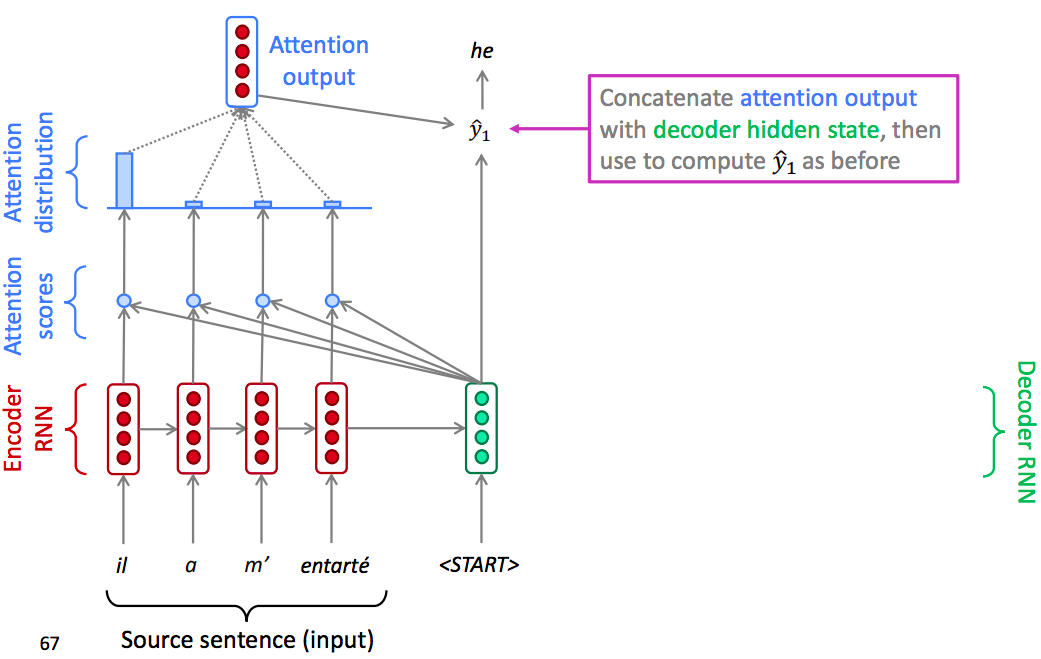
Finally Concatenate weighted sum of the encoder hidden states with decoder hidden state, then use to compute $\widehat{y}_{1}$ as before.
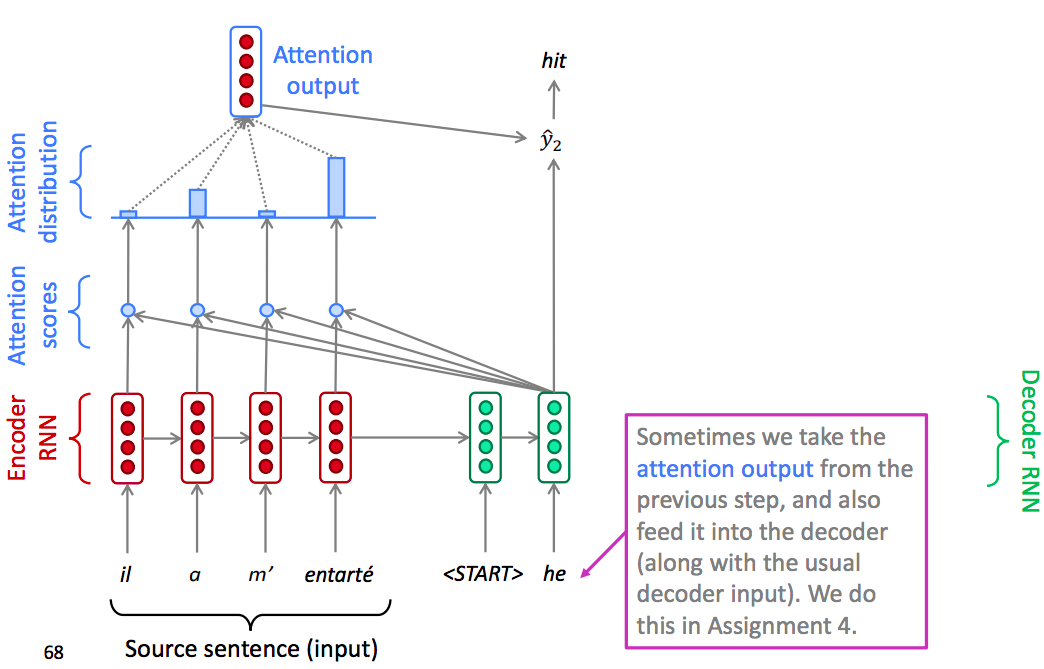
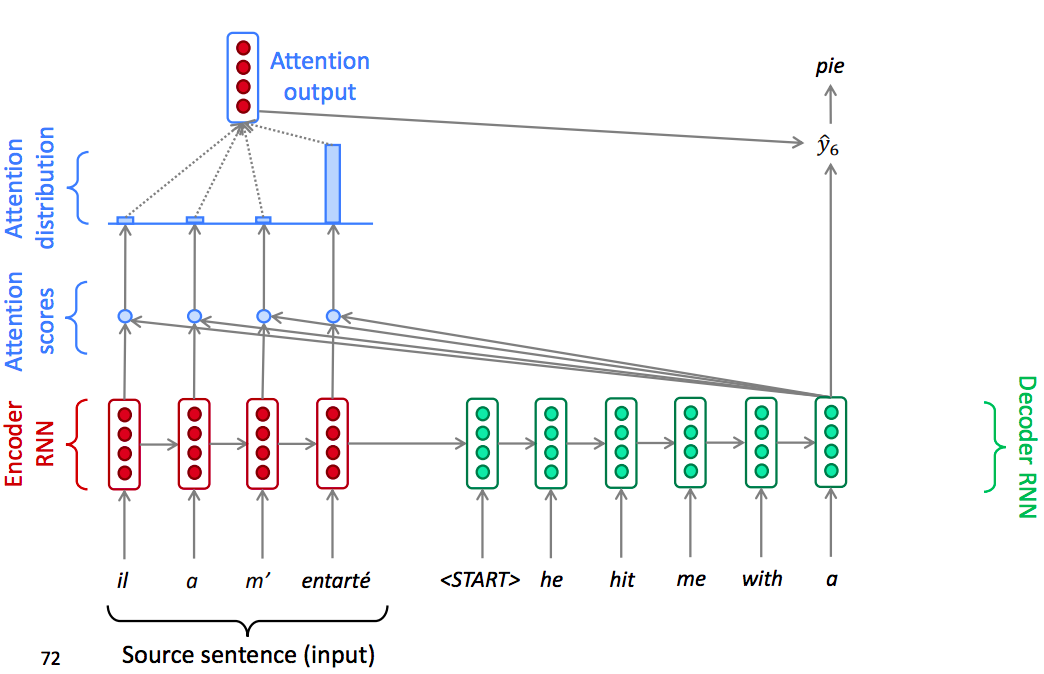
Attention in Equations
Remember that our seqzseq model is made of two parts, an encoder that encodes the input sentence, and a decoder that leverages the information extracted by the decoder to produce the translated sentence. Basically, our input is a sequence of words $x_1,…, x_n$ that we want to translate, and our target sentence is a sequence of words $y_1,…,y_m$.
Encoder
Let $(h_1,., h_n)$ be the hidden vectors representing the input sentence. These vectors are the output of a BI-LSTM for instance, ane capture contextual representation of each word in the sentence
Decoder
We want to compute the hidden states $s_i$ of the decoder using a recursive formula of the form
where $s_{i-1}$ is the previous hidden vector, $y_{i-1}$ is the generated word at the previous step, and $c_i$ is a context vector that capture the context from the original sentence that is relevant to the time step i of the decoder. The context vector $c_i$ captures relevant information for the i-th decoding time step (unlike the standard Seg2 seq in which theres only one context vector). For each hidden vector from the original sentence hi, compute a score
where a is any function, for instance a single layer fully-connected neural network. Then we end up with a sequence of scalar value $e_{i,1},…, e_{i,n}$. Normalize these scores into a vector $\alpha_{i}=\left(\alpha_{i, 1}, \ldots, \alpha_{i, n}\right)$, using a softmax layer.
Then, compute the context vector $c_i$ as the weighted average of the hidden vectors from the original sentence
Intuitively, this vector captures the relevant contextual information from the original sentence for the i-th step of the decoder.

Attention Variants


Conncetion with translation alignment
The attention-based model learns to assign significance to different parts of the input for each step of the output. In the context of translation, attention can be thought of as “alignment.” Bahdanau et al. argue that the attention scores aij at decoding step i signify the words in the source sentence that align with word i in the target. Noting this, we can use attention scores to build an alignment table – a table mapping words in the source to corresponding words in the target sentence – based on the learned encoder and decoder from our Seq2Seq NMT system.
